Презентация - Строение Солнечной системы. Законы движения планет

Строение Солнечной системы Законы движения планет Солнечной системы

Сегодня на уроке 1 Познакомимся с формулировками трёх законов Кеплера. 2 Узнаем, какую роль сыграли законы Кеплера для развития астрономии.

Титульная страница «De revolutionibus orbium coelestium» Николай Коперник 1473—1543 Небесные сферы в рукописи Коперника

Галилео Галилей 1564—1642 Движение небесных тел — это равномерное движение по окружности.

Венера, Меркурий и Луна в вечернем небе

Меркурий и Венера в вечернем небе

Иоганн Кеплер 1571—1630 В мире правит число!

Иоганн Кеплер 1571—1630 b 0 a 0 b 1 b 2 b 3 a 1 a 2 a 3 a 4 a 5 c 0 c 1 c 2 c 3 до ре ми фа соль ля си до 1

Иоганн Кеплер 1571—1630 «В геометрии имеются пять евклидовых тел, совершеннейший род фигур после сферы. По их образцу и прообразу устроена наша планетная система».

Иоганн Кеплер 1571—1630 «Кубок Кеплера»

Джон Холдейн 1892—1964 «Идея Вселенной как геометрически совершенного произведения искусства оказалась ещё одной прекрасной гипотезой, разрушенной уродливыми фактами».

Памятник Кеплеру и Тихо Браге, Прага

Книга Кеплера «De Stella Nova», 1604 г.

Иоганн Кеплер 1571—1630 Как по данным наблюдений определить орбиту и скорость движения других планет?

Модель Sunway Taihu Light — самый производительный суперкомпьютер в мире по состоянию на ноябрь 2016 г.

Иоганн Кеплер 1571—1630 Как по данным наблюдений определить орбиту и скорость движения других планет?

Марс

Тихо Браге 1546—1601

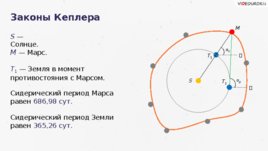
Законы Кеплера M — Марс. М Т 1 S α 1 Т 1 — Земля в момент противостояния с Марсом. S — Солнце. Сидерический период Марса равен 686,98 сут. Сидерический период Земли равен 365,26 сут. Т 2 α 2

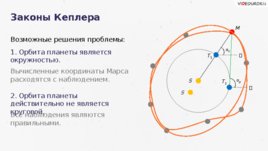
S Законы Кеплера М Т 1 S α 1 Т 2 α 2 Возможные решения проблемы: 1. Орбита планеты является окружностью. 2. Орбита планеты действительно не является круговой. Вычисленные координаты Марса расходятся с наблюдением. Все наблюдения являются правильными. S

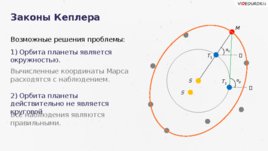
S Законы Кеплера М S α 1 Т 2 α 2 Возможные решения проблемы: 1) Орбита планеты является окружностью. 2) Орбита планеты действительно не является круговой Вычисленные координаты Марса расходятся с наблюдением. Все наблюдения являются правильными. S Т 1

Все планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце. И. Кеплер Первый закон Кеплера

Законы Кеплера Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется его большой осью. Отрезок, проходящий через центр эллипса перпендикулярно большой оси, называется малой осью эллипса. O F 1 F 2

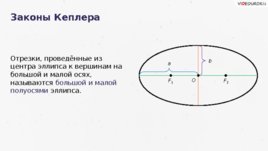
Законы Кеплера Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях, называются большой и малой полуосями эллипса. O F 1 F 2 a b

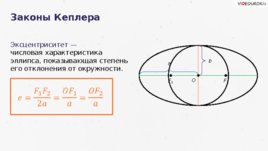
Законы Кеплера Эксцентриситет — числовая характеристика эллипса, показывающая степень его отклонения от окружности. O F 1 F 2 a b

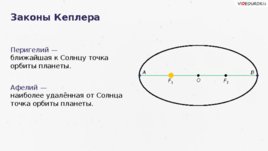
Законы Кеплера O F 1 F 2 Перигелий — ближайшая к Солнцу точка орбиты планеты. Афелий — наиболее удалённая от Солнца точка орбиты планеты. А В

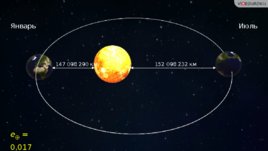
e 0,017 Январь Июль 147 098 290 км 152 098 232 км

Иоганн Кеплер 1571—1630

Радиус-вектор планеты за равные промежутки времени описывает равновеликие площади. И. Кеплер Второй закон Кеплера

Законы Кеплера Закон сохранения энергии: полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остаётся неизменной при любых движениях тел этой системы. к п

Законы Кеплера Скорость движения планеты по орбите меняется, принимая максимальное значение в перигелии и минимальное в афелии.

Иоганн Кеплер 1571—1630

Иоганн Кеплер 1571—1630 Первый закон Кеплера (1609): все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

Иоганн Кеплер 1571—1630 Первый закон Кеплера (1605): все планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце. Второй закон Кеплера (1602): радиус-вектор планеты за равные промежутки времени описывает равновеликие площади.

Квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит. И. Кеплер Третий закон Кеплера (1618 г.)

«То, что 16 лет тому назад я решил искать, наконец найдено, и это открытие превзошло все мои самые смелые ожидания...»

Квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит. И. Кеплер Третий закон Кеплера

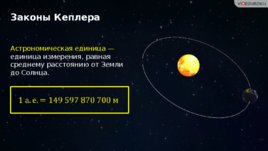
Законы Кеплера Астрономическая единица — единица измерения, равная среднему расстоянию от Земли до Солнца.

Первый закон Кеплера (1605): все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце. Второй закон Кеплера (1602): радиус-вектор планеты описывает в равные промежутки времени равновеликие площади. Третий закон Кеплера (1618): квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:

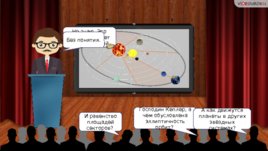
Господин Кеплер, а чем обусловлена эллиптичность орбит? И равенство площадей секторов? Не знаю. Это просто следует из наблюдений. А как движутся планеты в других звёздных системах? Без понятия.

Законы Ньютона Закон всемирного тяготения: любые два тела притягивают друг друга силами, прямо пропорциональными произведению масс этих тел и обратно пропорциональными квадрату расстояния между ними. Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.

Задача. Определите период обращения астероида Россия, если большая полуось его орбиты равна 2,55 а. е. РЕШЕНИЕ ДАНО ОТВЕТ: период обращения астероида Россия равен 4 годам. Третий закон Кеплера: Период обращения астероида: Так как , то , а

Выводы