Презентация - Расстояние между точками координатной прямой. Урок 35

1 Найдите модуль разности чисел p и n если: а) p 9,8, n 4,02 ; 9 ,8 – 4,02 5,78 5,78. 13 14 8 б) p , n ; 3 14 – 6 5 7 2 3 14 – 6 – 5 7 2 13 14 – 8

2 Запишите координаты точек А и В. Найдите длину отрезка АВ. Найдите модуль разности координат точек А и В. 0 1 A B а) A(4) B(10) AB 6 ; 4 – 10 – 6 6 . 6

2 Запишите координаты точек А и В. Найдите длину отрезка АВ. Найдите модуль разности координат точек А и В. A(– 7 ) B(– 2 ) AB 5; – 7 – ( –2) – 7 2 5. 0 1 A B б) 5

2 Запишите координаты точек А и В. Найдите длину отрезка АВ. Найдите модуль разности координат точек А и В. A(– 3 ) B( 6) AB 9; – 3 – 6 – 9 9. 0 1 A B в) 9

2 Запишите координаты точек А и В. Найдите длину отрезка АВ. Найдите модуль разности координат точек А и В. A(– 4 ) B( 2) AB 6; – 4 – 2 – 6 6. 0 1 A B г) 6

Проверка домашнего задания

№ 287 Найдите значение выражения – а – b , если: а) а 14 b 12; – а – b – 14 – 12 в) а 14 b – 12; – 26 б) а – 14 b 12; – а – b 14 – 12 2 – а – b – 14 – (– 12) – 14 12 – 2 г) а – 14 b – 12. – а – b 14 – (– 12) 14 12 26

№ 288 Вычислите: а) (– 18 – 21) (– 15 4) – 39 (– 11) – 50 б) (– 25 15) – (– 13 – 12) – 10 – (– 25) – 10 25 15 в) (0,8 – 1,4) (1,2 – 1,6) – 0,6 (– 0,4) – 1 г) (– 2,1 5,3) – (4,7 – 6,8) 3,2 – (– 2,1) 3,2 2,1 5,3

№ 289 Известно, что а и b – положительные числа. Сравните: а) 0 и а ; б) – а и b ; в) а и – а ; г) – b и а .

№ 29 1 ( б,г) Сколько целых чисел заключено между числами: б) – 15 и 0; 0 - 15 Ответ: 14 г) – 6 и 6. 6 - 6 Ответ: 11

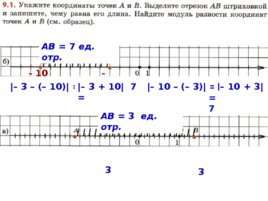
– 3 – (– 10 ) - 10 - 3 I I I I I I I I I I I I АВ 7 ед. отр. – 3 10 7 – 10 – (– 3 ) – 10 3 7 I I I I I I I I I I I I I I I I I I I I I АВ 3 ед. отр. 3 3

10/24/19 К л а с с н а я р а б о т а.

№ 2 93 Сравните значение выражения a – b и b – a при а 8, b 6; а – 8, b – 6; а – 8, b 6; а 8, b – 6. при а 8, b 6 a – b и b – a при а – 8, b – 6 a – b и b – a при а 8, b – 6 при а – 8, b 6 a – b и b – a a – b и b – a Какое предположение можно сделать? Значения выражений a – b и b – a рав-ны при любых значениях а и b .

– 3 – (– 10 ) - 10 - 3 I I I I I I I I I I I I АВ 7 ед. отр. – 3 10 7 – 10 – (– 3 ) – 10 3 7 Как найти расстояние между двумя точками?

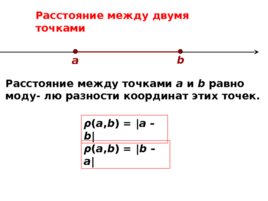
Расстояние между двумя точками b а Расстояние между точками а и b равно моду- лю разности координат этих точек. ρ ( а , b ) a – b ρ ( а , b ) b – a

№ 296(в,г) Найдите ρ ( х , у ), если: в) х 0,5 у 7,4; ρ ( х , у ) у – х 6,9 7,4 – 0,5 6,9 г) х 5,9 у – 6,8. ρ ( х , у ) у – х – 6,8 – 5,9 – 12,7 12,7

№ 297(в,г) На координатной прямой отмечены точки А ( х ) и В ( у ). Точка С – середина отрезка АВ . Найдите координату точки С , если: в) х – 2 у – 8; I I I I I I I I I I I I I I I I I О 0 В - 8 - 2 А С - 5 Как найти координату середины отрезка? 1) найти длину отрезка; 2) полученное число разделить на 2; 3) прибавить полученное число к левому концу или вычесть из правого. Ответ: С (– 5)

№ 297(в,г) На координатной прямой отмечены точки А ( х ) и В ( у ). Точка С – середина отрезка АВ . Найдите координату точки С , если: г) х 2 у – 8. АВ у – х – 8 – 2 – 10 10 10 : 2 5 – 8 5 или 2 – 5 – 3 – 3

№ 300(в) Вычислите: 7,41 : 10 – 6,92 7,46 – 0,741 0,692 10 – – 14,92 0,741 – 6,92 7,46 – 0,741 6,92 – 14,92 7,46 – 14,92 – 7,46

Дома: У: № 296(а,б); 297(а,б); 300(а,б); РТ: № 9.2; 9.4

Самостоятельная работа стр. 37 С – 9.2