Презентация - Плоскость

План лекции Преобразование чертежа плоскости 5 Задание плоскости на чертеже 1 Точка и прямая в плоскости 2 Положение плоскости в пространстве 3 Главные линии плоскости 4

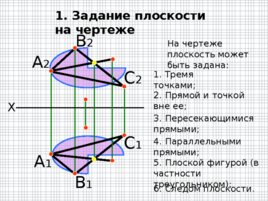
1. Задание плоскости на чертеже X А 2 В 2 А 1 В 1 С 2 С 1 1. Тремя точками; На чертеже плоскость может быть задана: 2. Прямой и точкой вне ее; 3. Пересекающимися прямыми; 4. Параллельными прямыми; 5. Плоской фигурой (в частности треугольником); 6. Следом плоскости.

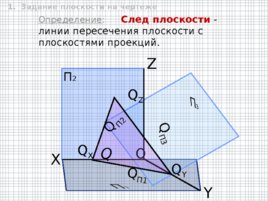
Определение : След плоскости - линии пересечения плоскости с плоскостями проекций. O П 2 X Y Z Q Q Z Q П2 Q X Q П1 Q Y Q П3 1. Задание плоскости на чертеже

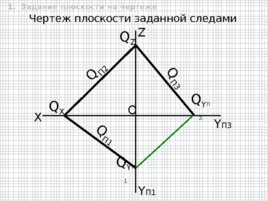
Чертеж плоскости заданной следами O X Q Z Q П2 Q X Q П1 Q Y П1 Q П3 Q Y П3 Y П3 Y П1 Z 1. Задание плоскости на чертеже

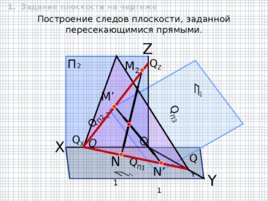
Построение следов плоскости, заданной пересекающимися прямыми. O П 2 X Y Z Q Q Z Q П2 Q X Q П1 Q Y Q П3 N 1 M 2 N 1 M 2 1. Задание плоскости на чертеже

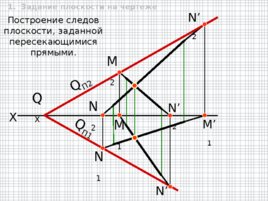
X Построение следов плоскости, заданной пересекающимися прямыми. N 1 N 1 N 2 N 2 Q П1 M 1 M 1 M 2 N 2 Q П 2 Q X 1. Задание плоскости на чертеже

2. Точка и прямая в плоскости Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости: Прямая принадлежит плоскости, если: 1) она проходит через две точки, лежащие в данной плоскости: или 2) она проходит через точку, принадлежащую плоскости, параллельно какой-нибудь прямой, лежащей в этой плоскости:

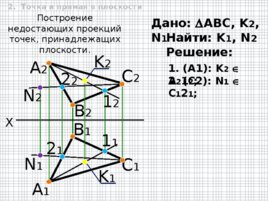
X А 2 В 2 А 1 В 1 С 2 С 1 1. (A1): K 2 A 2 1 2 ; Дано: АВС, K 2 , N 1 Построение недостающих проекций точек, принадлежащих плоскости. Найти: K 1 , N 2 Решение: K 2 N 1 1 2 1 1 K 1 2 . (C2): N 1 C 1 2 1 ; 2 1 2 2 N 2 2. Точка и прямая в плоскости

3. Положение плоскости в пространстве Плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения . Плоскости, параллельные или перпендикулярные плоскостям проекций, называются плоскостями частного положения .

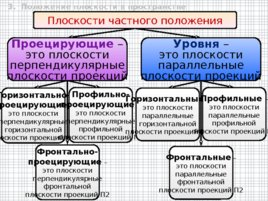
Плоскости частного положения Уровня – это плоскости параллельные плоскости проекций Горизонтально- проецирующие – это плоскости перпендикулярные горизонтальной плоскости проекций П1 Профильно- проецирующие – это плоскости перпендикулярные профильной плоскости проекций П3 Фронтально- проецирующие – это плоскости перпендикулярные фронтальной плоскости проекций П2 Горизонтальные – это плоскости параллельные горизонтальной плоскости проекций П1 Профильные – это плоскости параллельные профильной плоскости проекций П3 Фронтальные – это плоскости параллельные фронтальной плоскости проекций П2 Проецирующие – это плоскости перпендикулярные плоскости проекций 3. Положение плоскости в пространстве

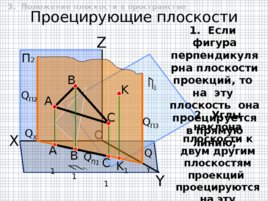
O Проецирующие плоскости П 2 X Y Z Q П2 Q X Q П1 Q Y Q П3 A 1 K K 1 A B C B 1 C 1 1. Если фигура перпендикулярна плоскости проекций, то на эту плоскость она проецируется в прямую линию ; 2. Углы наклона плоскости к двум другим плоскостям проекций п роецируются на эту плоско с ть в натуральную величину . 3. Положение плоскости в пространстве

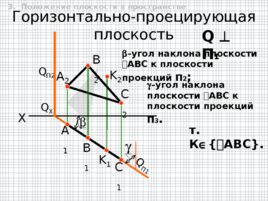
Горизонтально-проецирующая плоскость Q П2 Q X Q П1 A 1 K 2 K 1 B 1 C 1 X А 2 B 2 C 2 Q П 1 - угол наклона плоскости АВС к плоскости проекций П 2 ; - угол наклона плоскости АВС к плоскости проекций П 3 . т. К АВС . 3. Положение плоскости в пространстве

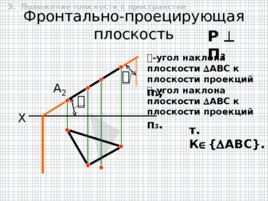
Фронтально-проецирующая плоскость X P П 2 - угол наклона плоскости АВС к плоскости проекций П 1 ; - угол наклона плоскости АВС к плоскости проекций П 3 . т. К АВС . 3. Положение плоскости в пространстве А 2

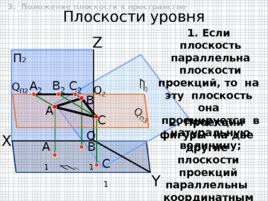
O Плоскости уровня П 2 X Y Z Q П2 Q Z Q П3 A 1 B 1 C 1 1. Если плоскость п араллельна плоскости проекций, то на эту плоскость она проецируется в натуральную величину; 2. Проекции фигуры на две другие плоскости проекций параллельны координатным осям . B C A A 2 B 2 C 2 3. Положение плоскости в пространстве

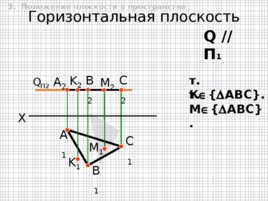
Горизонтальная плоскость Q П2 A 1 K 2 K 1 B 1 C 1 X А 2 B 2 C 2 Q // П 1 т. К АВС . т. M АВС . M 2 M 1 3. Положение плоскости в пространстве

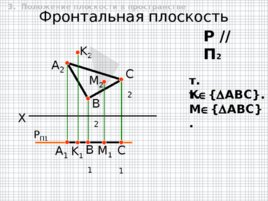
Фронтальная плоскость Р П1 A 2 K 1 K 2 B 2 C 2 X А 1 B 1 C 1 Р // П 2 т. К АВС . т. M АВС . M 1 M 2 3. Положение плоскости в пространстве

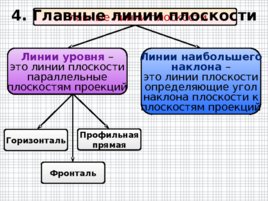
Главные линии плоскости Линии наибольшего наклона – это линии плоскости определяющие угол наклона плоскости к плоскостям проекций Горизонталь Профильная прямая Фронталь Линии уровня – это линии плоскости параллельные плоскостям проекций 4. Главные линии плоскости

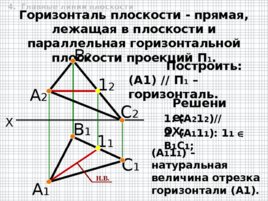
X А 2 В 2 А 1 В 1 С 2 С 1 1. (A 2 1 2 ) // OX ; Горизонталь плоскости - прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций П 1 . 1 2 1 1 2 . (A 1 1 1 ): 1 1 В 1 С 1 ; ( A1) // П 1 – горизонталь. (A 1 1 1 ) – натуральная величина отрезка горизонтали (А1). Построить: Решение: Н. В. 4. Главные линии плоскости

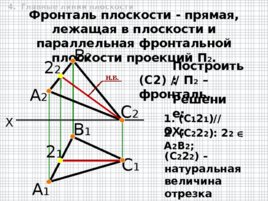
X А 2 В 2 А 1 В 1 С 2 С 1 1. ( С 1 2 1 ) // OX ; Фронталь плоскости - прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций П 2 . 2 2 2 1 2 . ( С 2 2 2 ): 2 2 А 2 В 2 ; (С2 ) // П 2 – фронталь. ( С 2 2 2 ) – натуральная величина отрезка фронтали (С2). Построить: Решение: Н. В. 4. Главные линии плоскости

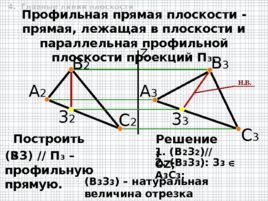
Z А 2 В 2 А 3 В 3 С 2 С 3 1. ( В 2 3 2 ) // OZ ; Профильная прямая плоскости - прямая, лежащая в плоскости и параллельная профильной плоскости проекций П 3 . 3 2 3 3 2 . (B 3 3 3 ): 3 3 А 3 C 3 ; ( B3) // П 3 – профильную прямую. (B 3 3 3 ) – натуральная величина отрезка профильной прямой ( B3 ). Построить: Решение: Н. В. 4. Главные линии плоскости

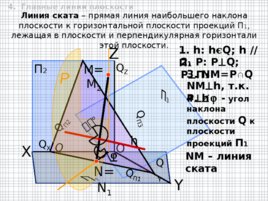
O П 2 X Y Z Q Z Q П2 Q X Q П1 Q Y Q П3 N N 1 Линия ската – прямая линия наибольшего наклона плоскости к горизонтальной плоскости проекций П 1 , лежащая в плоскости и перпендикулярная горизонтали этой плоскости. Q h P M M 2 º 1. h : h ϵ Q; h // П 1 2. Р: P Q; P П 1 3 . NM P Q NM h, т.к. Р h 4 . - угол наклона плоскости Q к плоскости проекций П 1 NM – линия ската 4. Главные линии плоскости

5. Преобразование чертежа плоскости 1. Проецирующую плоскость 2. Плоскость уровня Плоскость общего положения может быть преобразована в:

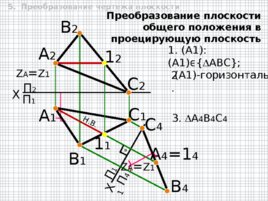
Преобразование плоскости общего положения в проецирующую плоскость 5. Преобразование чертежа плоскости П 2 Х 1 П 1 П 4 А 4 1 4 П 1 Z А Z 1 Н. В. X А 2 В 2 А 1 В 1 С 2 С 1 1 2 1 1 1. (A1) : (A1) ϵ ABC ; (A1)- горизонталь 2. 3. A 4 B 4 C 4 В 4 С 4 Z А Z 1

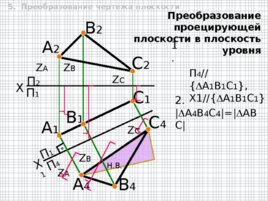
Преобразование проецирующей плоскости в плоскость уровня 5. Преобразование чертежа плоскости П 2 Х 1 П 1 П 4 А 4 П 1 Z А Н. В. X А 2 В 2 А 1 С 2 С 1 1. 2. A 4 B 4 C 4 ABC В 4 С 4 Z А В 1 П 4 // A 1 B 1 C 1 , Х1// A 1 B 1 C 1 Z B Z B Z C Z C

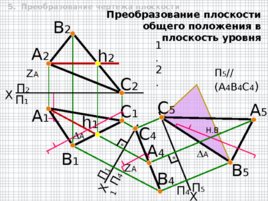
Преобразование плоскости общего положения в плоскость уровня 5. Преобразование чертежа плоскости П 2 Х 1 П 1 П 4 А 4 П 1 Z А X А 2 В 2 А 1 В 1 С 2 С 1 h 2 h 1 1 . В 4 С 4 Z А 2 . П 5 // (A 4 B 4 C 4 ) П 5 П 4 А А А 5 B 5 C 5 Н. В. Х 2