Презентация - Окружность.

Окружность
Учитель математик – Волкова А.С. Многопрофильный лицей №1 г. Магнитогорск 2021 год

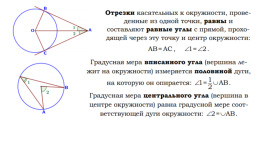
Свойства окружности
Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая). Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Хорда – отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд 1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

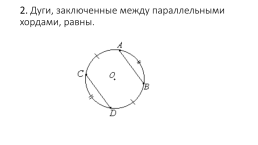
2. Дуги, заключенные между параллельными хордами, равны.

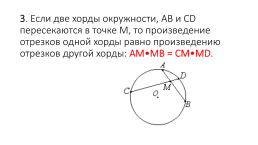
3. Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Длина окружности C радиуса R вычисляется по формуле: Площадь S круга радиуса R вычисляется по формуле: Длина дуги окружности L радиуса R с центральным углом измеренным в радианах, вычисляется по формуле: Площадь сектора радиуса R с центральным углом измеренным в радианах, вычисляется по формуле:

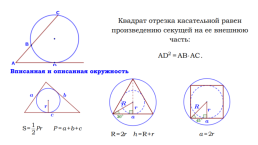
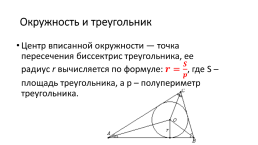
Окружность и треугольник
Центр вписанной окружности — точка пересечения биссектрис треугольника, ее радиус r вычисляется по формуле: , где S – площадь треугольника, а р – полупериметр треугольника.

Центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле: , здесь  a, b, c — стороны треугольника, - угол, лежащий против стороны a, S — площадь треугольника;

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы; Центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный.

Окружность и четырехугольники
Около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

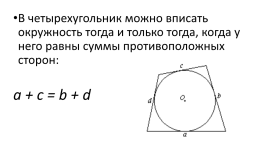
В четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон: a + c = b + d

Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником; Около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне; В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.