Презентация - Пример 1. Для пространственного стержня (рис. 1, А) опреде­лить значения и направления внутренних усилий в сечениях i—i и ii—ii.. Рис.1, А.. 1

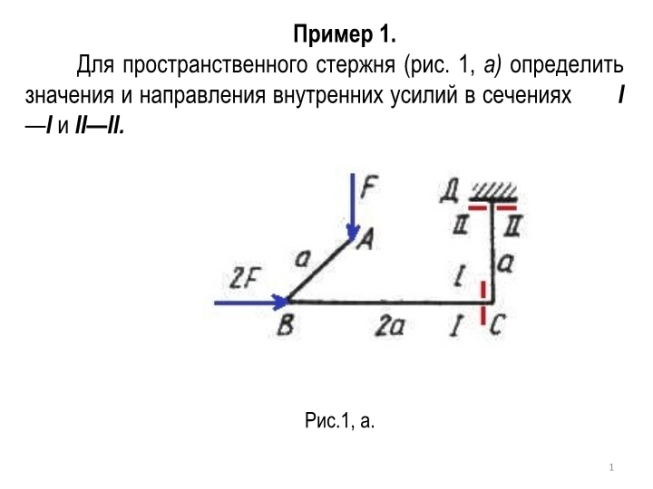
Пример 1. Для пространственного стержня (рис. 1, а) опреде­лить значения и направления внутренних усилий в сечениях I—I и II—II.
Рис.1, а.

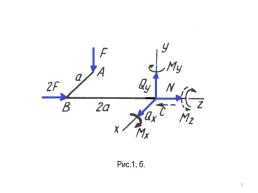
Решение. Для определения значений и направлений внутренних усилий в сечениях I—I и II—II применим метод сечений. Сечение I—I. Рассечем пространственный стержень в сечении I—I плоскостью, которая перпендикулярна оси стержня ВС (рис. 1, б). Одну часть стержня, например содержащую заделку, отбросим и дейст­вие ее на оставшуюся часть заменим шестью внутренними усилиями N, Qx, Qy и Mz, Мх, My, приложенными в сечении I—I .

Рис.1, б.

Выберем прямоугольную систему осей х, у, z, совместив начало координат с центром тяжести сечения I—I . Ось z направим вдоль оси рассеченного стержня ВС (в сторону внешней нормали сече­ния), а оси х и у расположим в плоскости его поперечного сечения, как показано на рис. 1,б. Такой выбор осей является обязательным.

Внутренние усилия Qx, Qy и N направим вдоль соответствующих поло­жительных осей х, у, z, внутренние усилия Мх, Му и Мz — по ходу часовой стрелки при взгляде на оставшуюся часть со стороны положи­тельного направления тех же осей. Такие направления внутренних сило­вых факторов будем считать положительными. Часть стержня, нагруженная внешними силами F, 2F и усилиями, приложенными в сечении /—/, находится в равновесии (рис. 1, б).

Для этой части стержня составим шесть уравнений равновесия, из решения которых определим внутренние усилия в сечении /—/: ост.ч ост.ч . ост.ч = 0; Qx= 0; = 0, Qy – F = 0, Qy = F; = 0, N + 2F=0, ост.ч. ост.ч. N = - 2F; = 0, Mx- F2a=0, Mx=2Fa; =0, My=0; ост.ч. = 0, Mz + Fa =0, Mz = - Fa. Таким образом, в сечении I—I действует четыре внутренних усилия (Qx=0 и Му =0), причем два из них — N и Mz— в направлении, противоположном принятому (на рис. 1, б действительные направле­ния их показаны пунктиром).

Сечение II—II. Рассечем стержень в сечении II—II плоскостью, перпендикулярной оси стержня CD. Часть стержня, содержащую жест­кое закрепление, отбросим. Выберем систему координат х, у, z и дейст­вие отброшенной части на оставшуюся заменим шестью внутренними усилиями, как показано на рис. 1, в.
Рис.1, в.

Эта часть стержня находится в равновесии; составим для нее уравнения равновесия: ост .ч. ост.ч. ост.ч. = 0, QX + 2F = 0, Qx = - 2F; = 0, Qy = 0; = 0, N – F = 0, N = F; ост.ч. ост.ч. = 0, Mx + Fa = 0, Mx = - Fa; = 0, ост.ч. My - F2a - 2Fa = 0, My = 4Fa; = 0, Mz = 0. Следовательно, в сечении II—II возникает четыре внутренних уси­лия (Qy = 0, Mz = 0), причем два из них — Qx и Мх — направлены в об­ратную сторону (рис. 1, в).