Презентация - Кодирование числовой информации

Кодирование числовой информации

Система счисления
Для записи информации о количестве объектов используются числа. Числа записываются с помощью набора специальных символов. Система счисления — знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Виды систем счисления
Все системы счисления делятся на две большие группы:
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
Количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. 0,7; 7; 70
Количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. XIX

Непозиционные системы счисления
Каноническим примером фактически непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы: I обозначает 1, V - 5, X - 10, L - 50, C - 100, D - 500, M -1000. Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII. MCMLXXXVIII = 1000+(1000-100)+(50+10+10+10)+5+1+1+1 = 1988

Позиционные системы счисления
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции). Количество используемых цифр называется основанием системы счисления. Например, 11 – это одиннадцать, а не два: 1 + 1 = 2 (сравните с римской системой счисления). Здесь символ 1 имеет различное значение в зависимости от позиции в числе.

Первые позиционные системы счисления
Самой первой такой системой, когда счетным "прибором" служили пальцы рук, была пятеричная. Некоторые племена на филиппинских островах используют ее и в наши дни, а в цивилизованных странах ее реликт, как считают специалисты, сохранился только в виде школьной пятибалльной шкалы оценок.

Двенадцатеричная система счисления
Следующей после пятеричной возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Некоторые учёные полагают, что такая система возникала у них из подсчёта фаланг на руке большим пальцем. Широкое распространение получила двенадцатеричная система счисления в XIX веке. На ее широкое использование в прошлом явно указывают названия числительных во многих языках, а также сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов. Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия: 1 дюжина = 12 штук; 1 гросс = 12 дюжин = 144 штуки; 1 масса = 12 гроссов = 144 дюжины = 1728 штук. Английский фунт состоит из 12 шиллингов.

Шестидесятеричная система счисления
Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр! В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.

Какие позиционные системы счисления используются сейчас?
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления. Двоичная, восьмеричная (в настоящее время вытесняется шестнадцатеричной) и шестнадцатеричная система часто используется в областях, связанных с цифровыми устройствами, программировании и вообще компьютерной документации. Современные компьютерные системы оперируют информацией представленной в цифровой форме. Числовые данные преобразуются в двоичную систему счисления.

Десятичная система счисления
Десятичная система счисления — позиционная система счисления по основанию 10. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.

Двоичная система счисления
Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах.

Восьмеричная система счисления
Восьмеричная система счисления — позиционная система счисления с основанием 8. Используются цифры 0, 1, 2, 3, 4, 5, 6 ,7.

Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — позиционная система счисления с основанием 16. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Система счисления.Осно-вание.Алфавит цифр
Десятичная.10.0, 1, 2, 3, 4, 5, 6, 7,8, 9
Двоичная.2.0, 1
Восьмеричная.8.0, 1, 2, 3, 4, 5, 6, 7
Шестнадцате- ричная.16.0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14), F (15)

Перевод чисел из одной системы счисления в другую
Чтобы перевести число из позиционной системы счисления с основанием p в десятичную, надо представить это число в виде суммы степеней p и произвести указанные вычисления в десятичной системе счисления.

Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.

Домашнее задание:
Запишите число 1945 в римской системе счисления. Переведите в десятичную систему числа: 10111102, 1278 , 2D516 , 101,112. Переведите в двоичную, восьмеричную и шестнадцатеричную систему числа: 14110 , 37910.

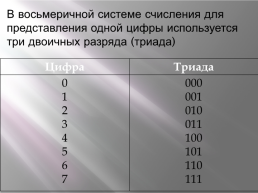
В восьмеричной системе счисления для представления одной цифры используется три двоичных разряда (триада)
Цифра.Триада
0 1 2 3 4 5 6 7.000 001 010 011 100 101 110 111

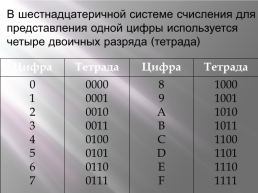
В шестнадцатеричной системе счисления для представления одной цифры используется четыре двоичных разряда (тетрада)
Цифра.Тетрада.Цифра.Тетрада
0 1 2 3 4 5 6 7.0000 0001 0010 0011 0100 0101 0110 0111.8 9 A B C D E F.1000 1001 1010 1011 1100 1101 1110 1111