Презентация - Математика и искусство

Автор: Пахомов Егор(Pachomow Egor) Рукотель: Градежда Леся Дмитриевна Тел.8(929)6527104, lesya.25@mail.ru МОУ СОШ№6 г.Раменское, ул.Серова д.18.
Математика и искусство

Математика Искусство Роль математики в искусстве Многоугольники (картинки) Тесселяция Невозможные фигуры Лист Мёбиуса Фракта́л Мат-метал Вывод

Матема́тика (от др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы

Иску́cство (от церк.-слав. искусьство (лат. eхperimentum — опыт, проба); ст.-слав. искоусъ — опыт, реже истязание, пытка) — образное осмысление действительности; процесс или итог выражения внутреннего или внешнего мира творца в (художественном) образе; творчество, направленное таким образом, что оно отражает интересующее не только самого автора, но и других людей. Искусство (наряду с наукой) — один из способов познания, как в естественнонаучной, так и в религиозной картине восприятия мира. Понятие искусства крайне широко — оно может проявляться как чрезвычайно развитое мастерство в какой-то определённой области. Долгое время искусством считался вид культурной деятельности, удовлетворяющий любовь человека к прекрасному. Вместе с эволюцией социальных эстетических норм и оценок искусством получила право называться любая деятельность, направленная на создание эстетически-выразительных форм. В масштабах всего общества, искусство — особый способ познания и отражения действительности, одна из форм художественной деятельности общественного сознания и часть духовной культуры как человека, так и всего человечества, многообразный результат творческой деятельности всех поколений.

Исторически, математика играла важную роль в изобрази-тельном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам. Вообще-то не существует каких-либо правил или ограничений на использование различных тем в математическом искусстве. Однако, есть несколько тем, которые достаточно часто различным художниками. Среди них есть использование многогранников, тесселяций, невозможных фигур, лент Мебиуса, искаженных или необычных систем перспективы, а также фракталов.

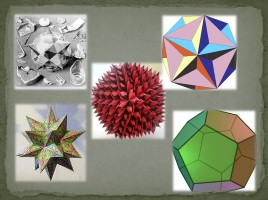
Многогранником называется тело, граница которого является объединением конечного числа многоугольников. Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном програм-мировании, теории оптимального управления. Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. Они обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед. Многогранники выделяются необычными свойствами, самое яркое из которых формулируется в теореме Эйлера о числе граней, вершин и ребер выпуклого многогранника: для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г-число граней, В-число вершин, Р-число ребер данного много-гранника. Теорему Эйлера историки математики называют первой теоремой топологии - крупного раздела современной математики.

Тесселя́ция (англ. tessellation) в переводе с английского, означает мозаика . Тесселяция или разбиение плоскости картины, которая заполняет плоскость без каких-либо накладок и без пробелов. В латинском tessella небольшой кусочек глины, камня или стекла используется для изготовления мозаики. Слово «tessella" означает "маленький квадрат.

Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозмож-ности существования такой фигуры в трёхмерном прост-ранстве. На самом деле все невозможные фигуры могут существовать в реальном мире. Так, все объекты, нарисованные на бумаге, являются проекциями трёхмерных объектов, следовательно, можно создать такой трёхмерный объект, который при проецировании на плоскость будет выглядеть невозможным. При взгляде на такой объект из определённой точки он также будет выглядеть невозможным, но при обзоре с любой другой точки эффект невозможности будет теряться.

Лист Мёбиуса (ле́нта Мёбиуса, петля́ Мёбиуса) — топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное евклидово пространство R³. Попасть из одной точки этой поверхности в любую другую можно, не пересекая края.

Лента Мёбиуса была открыта независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году. Модель ленты Мёбиуса может легко быть сделана. Для этого надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них. В евклидовом пространстве существуют два типа полос Мёбиуса в зависимости от направления закручивания: правые и левые (топологически они, однако, неразличимы).

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической.

Мат-метал (англ. math metal — математический метал) — подстиль хэви-метала, характеризующийся сложным построением композиций, использованием нестандартных музыкальных размеров. Как правило, появляются ритмические сбивки, когда сильная доля нарочно переносится на слабую путем урезания или удлинения фразы вместе с увеличением/уменьшением размерности для одного из инструментов в каком-либо одном такте нужной фразы. Сложные структуры, обилие полиритмии, нестандартные гармонии, смещение акцентов, нестандартные размеры тактов — это главные составляющие мат-метала как такового. Вместе с тем мат-метал сохраняет черты, присущие грув-металу — акцент на ритм-гитару и ударные в ритме 4/4.

Математические изобразительное искусство процветает сегодня, и многие художники создают картины в стиле Эшера и в своем собственном стиле. Эти художники работают в различных направлениях, включая скульптуру, рисование на плоских и трехмерных поверхностях, литографию и компьютерную графику. А наиболее популярными темами математического искусства остаются многогранники, тесселляции, невозможные фигуры, ленты Мебиуса, искаженные системы перспективы и фракталы.

http://ru.wikipedia.org http://images.yandex.ru
Используемая литература

СПАСИБО ЗА ВНИМАНИЕ!