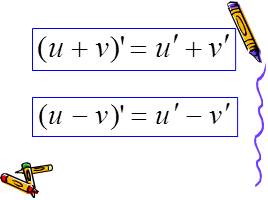Слайды и текст этой онлайн презентации
Слайд 1
Тема урока:
«Производная суммы»
Слайд 2
Цели урока
обобщить и систематизировать материал темы по применению таблицы производных;
научить применять правило производной суммы при решении задач;
развивать познавательный интерес учащихся, совершенствовать умения применять знания в измененной ситуации;
воспитывать аккуратность и внимательность при оформлении заданий;
Слайд 3
Синусом
Уравнением
Математикой
Метр
Алгоритм
С
У
М
М
А
Терминологический диктант
Слайд 4
Алгоритм нахождения производной
Слайд 5
Алгоритм нахождения производной
В данной функции от х, нареченной у
Вы фиксируете х, отмечая индексом х0
Придаёте вы ему тотчас приращение х0+Δх
Тем у функции самой, вызвав изменение
Приращений тех теперь взявши отношение
Побуждаете к нулю у Δх стремление Δх→0
Предел такого отношения вычисляется
Он производною в науке называется
Слайд 6
Таблица производных.
Слайд 8
ЛАГРАНЖ Жозеф Луи (1736-1813)
Французский математик и механик.
Член Парижской Академии наук.
Труды в области аналитической и теоретической механики.
Предложил аналитический метод для решения вариационных задач.
Проводил исследования по вопросам математического анализа, теории чисел, дифференциальным уравнениям.
Работал в области астрономии и других наук.
Слайд 10
Физический смысл производной
Слайд 11
Пример решения физической задачи
Дано уравнение движения тела
Найти v(t), a(t).
Слайд 12
Правила эстафеты
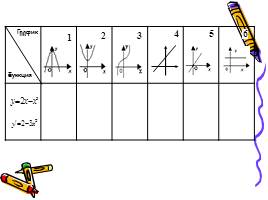
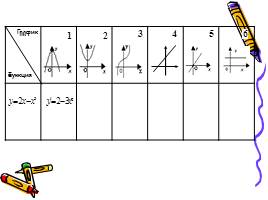
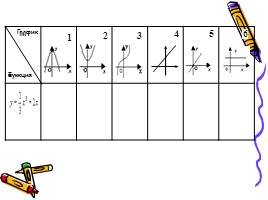
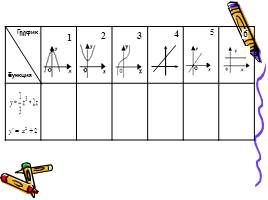
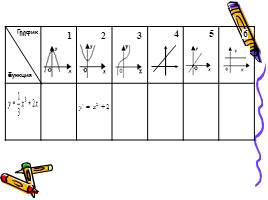
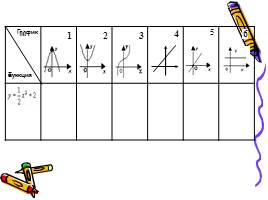
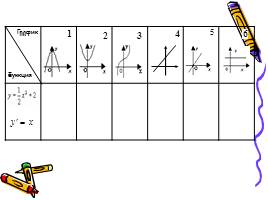
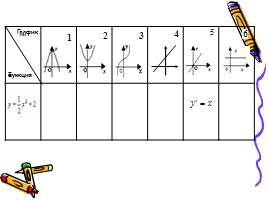
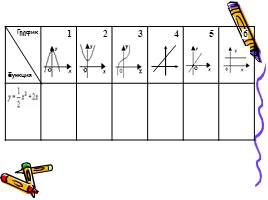
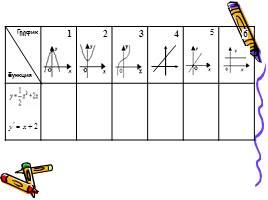
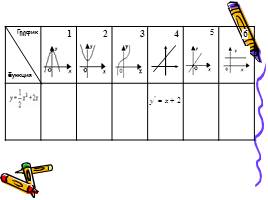
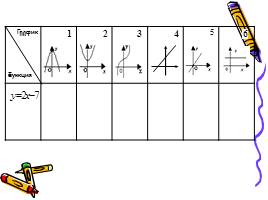
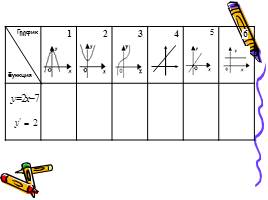
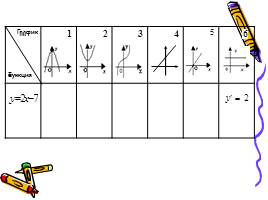
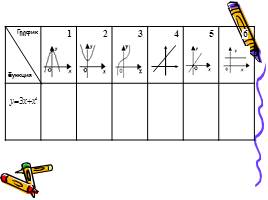
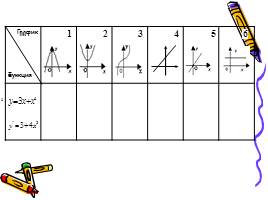
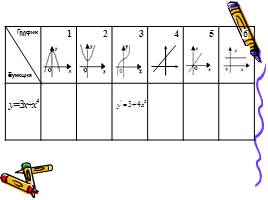
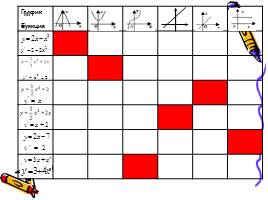
1 этап: нахождение производной функции
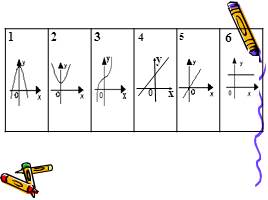
2 этап: нахождение координат графика
3 этап: построение эскиза графика
4 этап: проверка, выбор и защита решения
Слайд 33
Вопросы к закреплению
Сформулируйте правило производной суммы.
Сформулируйте частный случай производной суммы.
В каких науках используется производная для решения задач.
Слайд 34
Домашнее задание
№ 208 (в, г) стр. 114
№ 213 (в, г) стр. 114
Дополнительное задание
№ 212 (а, б, в) стр.114
 Своя игра. Применение производной
Своя игра. Применение производной Разложение на множители с помощью формул квадрата суммы и квадрата
Разложение на множители с помощью формул квадрата суммы и квадрата Слитное и раздельное написание производных предлогов
Слитное и раздельное написание производных предлогов Русский язык 7 класс «Слитное и раздельное написание производных отымённых предлогов»
Русский язык 7 класс «Слитное и раздельное написание производных отымённых предлогов» Урок русского языка в 7 классе «Слитное и раздельное написание производных предлогов»
Урок русского языка в 7 классе «Слитное и раздельное написание производных предлогов» Слагаемые и значение суммы
Слагаемые и значение суммы Формулы производных
Формулы производных