Презентация - Элементарные функции

Элементарные функции
Урок №1

Функция – это одно из основных математических и общенаучных понятий , выражающее зависимость между переменными величинами. Каждая область знаний: физика, химия, биология, социология, лингвистика и т.д. – имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов.

В различных науках и областях человеческой деятельности возникают количественные соотношения, и математика изучает их в виде свойств чисел. Математика рассматривает абстрактные переменные величины и в отвлеченном виде, изучает различные законы их взаимосвязи, которые на математическом языке называются функциональными зависимостями, или функциями.

Определение:
06.09.2016
http://aida.ucoz.ru
4
Пусть даны два множества Х и Y. Определение 1. Если каждому элементу х из множества Х по определённому правилу или закону f ставится в соответствие один элемент у из множества Y, то говорят, что на множестве Х задана функция f и пишут , или у = f(x).

Определение:
06.09.2016
http://aida.ucoz.ru
5
, или у = f(x). При этом величина х называется аргументом функции f, а множество Х – областью определения функции f. Величина х называется также независимой переменной, а величина у – зависимой переменной. Множество Y называется областью значений функции f. Область определения функции f обозначается через D(f), а область значений – через E(f).

Способы задания функции:
Задать функцию – значит указать область её определения и правило, по которому по данному значению независимой переменной можно найти соответствующее ему значение функции. Существует три основных способа задания функции:  аналитический,  табличный,  графический.

Определение:
06.09.2016
http://aida.ucoz.ru
7
у = f(x) (1) Число, соответствующее для данной функции у(х), называют значением функции в точке х0 и обозначают у(х0) Если функция записана в виде (1), то число обозначают f(х0).

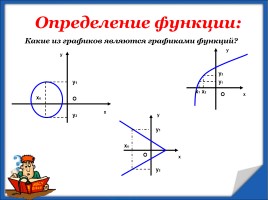
Определение функции:
Какие из графиков являются графиками функций?

Способы задания функции:
аналитический табличный графический
зависимость между переменными величинами задаётся с помощью формулы, указывающей, какие действия надо выполнить над аргументом, чтобы получить соответствующее ему значение функции. При этом функция может быть задана как одной формулой, например, так и несколькими формулами, например заключается в том, что зависимость между переменными задают с помощью таблицы. Хорошо известны, например, таблицы логарифмов, тригонометрических функций и др. состоит в том, что соответствие между переменными х и у задаётся с помощью графика функции. Графиком функции y = f(x) называется множество всех точек (х, у) плоскости XOY, координаты которых связаны соотношением y = f(x). Так, графики вышеназванных функций: f(x) и g(x)
х 0 1 2 3 4
у 0 1 4 9 16

Сложная функция
06.09.2016
http://aida.ucoz.ru
10
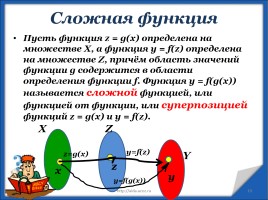
Пусть функция z = g(x) определена на множестве Х, а функция y = f(z) определена на множестве Z, причём область значений функции g содержится в области определения функции f. Функция y = f(g(x)) называется сложной функцией, или функцией от функции, или суперпозицией функций z = g(x) и y = f(z).
y=f(g(x))
Y

Сложная функция
06.09.2016
http://aida.ucoz.ru
11
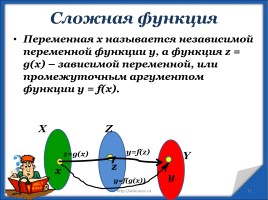
Переменная х называется независимой переменной функции у, а функция z = g(x) – зависимой переменной, или промежуточным аргументом функции y = f(x).
y=f(g(x))
Y

Примеры:
z=g(x) y=f(z) y=f(g(x))
06.09.2016
http://aida.ucoz.ru
12

Примеры сложных функций
Можно указать сложную функцию, в образовании которой участвует более двух функций. Например:
06.09.2016
http://aida.ucoz.ru
13

Элементарные функции
Основными элементарными функциями называются следующие функции: степенная функция показательная функция логарифмическая функция , тригонометрические функции
06.09.2016
http://aida.ucoz.ru
14

Элементарные функции
ОПРЕДЕЛЕНИЕ. Элементарной функцией называется функция, которая может быть задана одной формулой у = f(x) , где f(x) – выражение, составленное из основных элементарных функций и действительных чисел с помощью конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
06.09.2016
http://aida.ucoz.ru
15

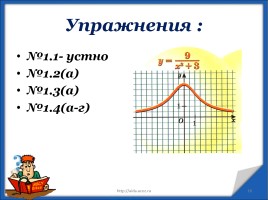
Упражнения :
№1.1- устно №1.2(а) №1.3(а) №1.4(а-г)
06.09.2016
http://aida.ucoz.ru
16

Домашнее задание:
п.1.1- читать №1.2(б) №1.3(б) №1.4(д-з)
06.09.2016
http://aida.ucoz.ru
17