Презентация - Теорема Пифагора

ТЕОРЕМА ПИФАГОРА
Геометрия, 8 класс
Алексеева Валентина Александровна, учитель математики ГБОУ СОШ № 404 Колпинского района Санкт-Петербурга

«Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.» Иоганн Кеплер

Цели
Образовательные: организовать деятельность учащихся по применению теоретических знаний к решению задач. Обеспечить условия для продуктивной, познавательной деятельности при решении задач конструктивного и творческого уровней. Развивающие: создать условия для развития у учащихся интереса к предмету геометрии и её истории. Содействовать быстрой актуализации и практическому применению полученных знаний, умений и способов действий в нестандартной ситуации. Воспитательные: содействовать формированию у учащихся ответственности за свою деятельность.

Оборудование
Л.С. Атанасян. Геометрия 7-9. Учебник средней школы. М., Просвещение, 2009 Персональный компьютер. Мультимедиа проектор Рабочие тетради учащихся Чертёжные принадлежности

Легенды о Пифагоре

Родился Пифагор где-то между 600 и 590 гг. до Рождества Христова и жил около ста лет. Много странных легенд дошло до наших дней о его рождении. Некоторые из них утверждают, что он не был обычным смертным человеком, а был одним из богов, принявших человеческий облик для того, чтобы войти в мир и учить человечество.

За 1000 лет античной традиции реальные и вызывающие глубокое уважение к личности Пифагора сведения были перемешаны со множеством легенд, сказок и небылиц. Легенды наперебой объявляли Пифагора чудотворцем; сообщали, что у него было золотое бедро, что люди видели его одновременно в двух разных городах говорящим со своими учениками, что однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и громким сверхчеловеческим голосом воскликнула: «Да здравствует Пифагор!», что в Тиррении он умертвил своим укусом ядовитую змею, унесшую жизни многих тирренцев, что он предсказывал землетрясения, останавливал повальные болезни, отвращал ураганы, укрощал морские волны.

Порфирий рассказывает о Пифагоре такую историю: в «Таренте он увидел быка на разнотравье, жевавшего зеленые бобы, подошел к пастуху и посоветовал сказать быку, чтобы тот этого не делал. Пастух стал смеяться и сказал, что не умеет говорить по-бычьи; тогда Пифагор сам подошел к быку и прошептал ему что-то на ухо, после чего тот не только тут же пошел прочь от бобовника, но и более никогда не касался бобов, а жил с тех пор и умер в глубокой старости в Таренте при храме Геры, где слыл священным быком и кормился хлебом, который давали ему прохожие».

Диоген Лаэртский, например, рассказывает так: «Появившись в Италии, Пифагор устроил себе жилье под землей, а матери велел записывать на дощечках всё, что происходит и когда, а дощечки спускать к нему, пока он не выйдет. Мать так и делала; а Пифагор, выждав время, вышел, иссохший, как скелет, предстал перед народным собранием и заявил, будто пришел из Аида, а при этом прочитал им обо всём, что с ними случилось. Все были потрясены прочитанным, плакали и рыдали, а Пифагора почли Богом. И тем не менее основной тон всех преданий о Пифагоре был один: «Ни о ком не говорят так много и так необычайно» (Порфирий).

О смерти Пифагора известно мало, существует как минимум три версии ухода великого ученого. Одна из них гласит, что когда был подожжён дом Милона в Кротоне, где собрались пифагорейцы, когда стали рушиться подпорки и перекрытия, державшие крышу, Пифагор в задумчивости сидел в центре большой залы. Великий мудрец и не помышлял сделать хоть одно движение к своему спасению. Тогда ученики Пифагора бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам, как по мосту, вышел из объятого пламенем дома. Пифагора спасли, но страшной ценой - ценой жизней его единомышленников. Оставшись один, Пифагор так затосковал, что удалился из города и там лишил себя жизни. Жизнь без продолжателей учения была для Пифагора лишена смысла.

Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придётся сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принёс в жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя ещё Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики.

Оптимист Михайло Ломоносов (1711-1765) писал: «Пифагор за изобретение одного геометрического правила Зевсу принёс в жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».

Ироничный Генрих Гейне (1797-1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не может доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принёс в жертву бессмертным богам».

Различные формулировки теоремы Пифагора

У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

Латинский перевод арабского текста Аннаирици (около 900 г. до н.э.), сделанный Герхардом Кремонским (начало 12 в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".

В Geometria Culmonensis (около 1400 г.) теорема читается так: Also, wird das vierecke Feld, gemessen an der langen Wand, so also gross ist als bei beide Vierecke, bei zwei werden gemessen von den zwei Wanden des deren, bei zwei gemeinde, tretten in dem rechten Winkel. В переводе это означает: "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".

В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. 3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.    

Теорема Пифагора в стихах
Если дан нам треугольник и притом, с прямым углом, То квадрат гипотенузы мы всегда легко найдем: Катеты в квадрат возводим, сумму степеней находим – И таким простым путем к результату мы придем.

Как символ вечного союза, как верной дружбы знак простой Связала ты гипотенуза навеки катеты с собой. Путей окольных избегая и древней истине верна, Ты по характеру – прямая, и по обычаю точна. Скрывала тайну ты, но скоро явился некий мудрый грек. И теоремой Пифагора тебя прославил он навек. Хранит тебя безмолвно, чинно углов сторожевой наряд; И копья – острые вершины – по обе стороны грозят. И, если двоечник, конфузясь, немеет пред твоим лицом, Пронзи его гипотенуза своим отточенным копьем!

Теорема Пифагора в решении исторических и занимательных задач

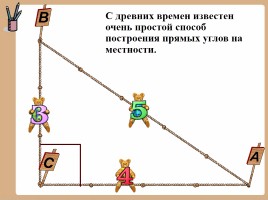
С древних времен известен очень простой способ построения прямых углов на местности.

Этот способ применялся тысячелетия назад строителями египетских пирамид

Задача индийского математика XII века Бхаскара Акария
На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?

Задача о бамбуке из древнекитайского трактата "Гоу-гу"
Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи). Какова высота бамбука после сгибания?

Задача из китайской «Математики в девяти книгах»
Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?

Египетская задача о лотосе
На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну.

Задача из учебника «Арифметика» Леонтия Магницкого
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.

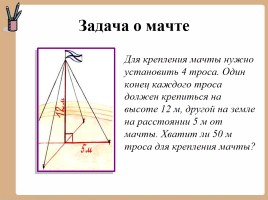
Задача о мачте
Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

Древняя индийская задача
Над озером тихим С полфута размером Высился лотоса цвет. Он рос одиноко, И ветер порывом Отнёс его в сторону. Нет Боле цветка над водой. Нашёл же рыбак его Ранней весною В двух футах от места, где рос. Итак, предложу я вопрос: “Как озера вода здесь глубока?”

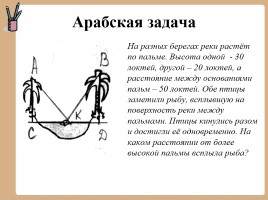
Арабская задача
На разных берегах реки растёт по пальме. Высота одной - 30 локтей, другой – 20 локтей, а расстояние между основаниями пальм – 50 локтей. Обе птицы заметили рыбу, всплывшую на поверхность реки между пальмами. Птицы кинулись разом и достигли её одновременно. На каком расстоянии от более высокой пальмы всплыла рыба?  

Задача о башнях
Одна из башен в полтора раза выше другой. Расстояние между основаниями башен равно 120 метров, а между шпилями – 125 метров. Чему равна высота каждой башни?

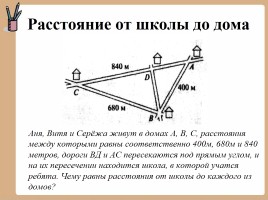
Расстояние от школы до дома
Аня, Витя и Серёжа живут в домах А, В, С, расстояния между которыми равны соответственно 400м, 680м и 840 метров, дороги ВД и АС пересекаются под прямым углом, и на их пересечении находится школа, в которой учатся ребята. Чему равны расстояния от школы до каждого из домов?

Задача о наблюдателе
Как далеко видит вокруг себя наблюдатель, находящийся на воздушном шаре на высоте 10 км над землёй? (R = 6400км)

Решение задач на применение теоремы Пифагора на готовых чертежах

8
9
10
11
12
14
15
16
17
18
20
21
22
23
24
30
29
28
27
26
1
2
3
4
5
6
13
19
25
7

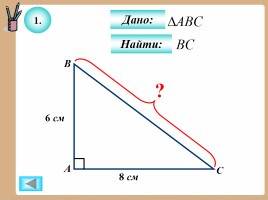
1.
Найти:
Дано:

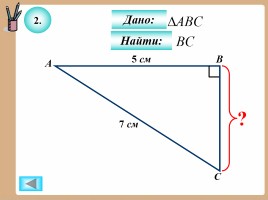
2.
Дано:
Найти:

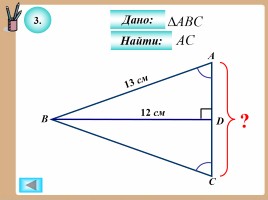
3.
Дано:
Найти:

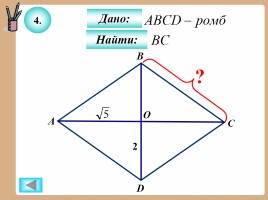
4.
Дано:
Найти:

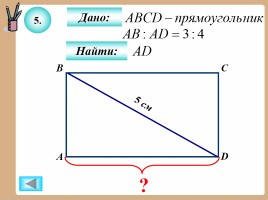
5.
Дано:
Найти:

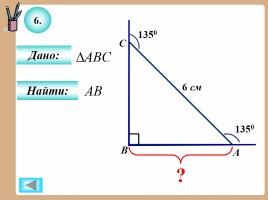
6.
Дано:
Найти:

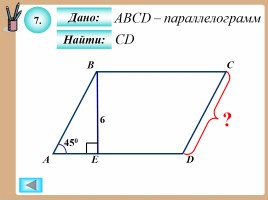
7.
Найти:
Дано:

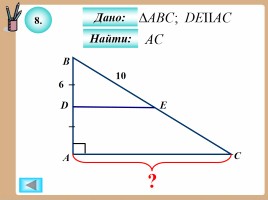
8.
Найти:
Дано:

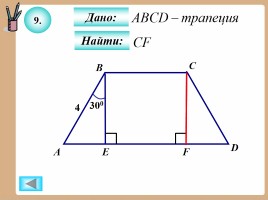
9.
Дано:
Найти:

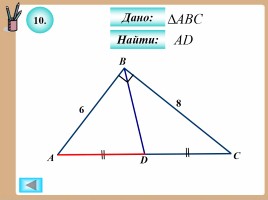
10.
Дано:
Найти:

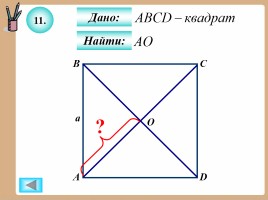
11.
Найти:
Дано:

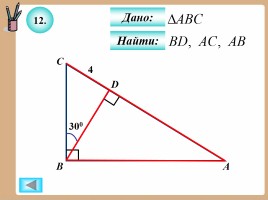
12.
Найти:
Дано:

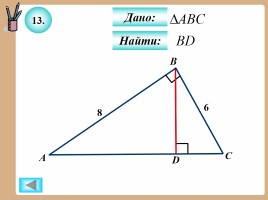
13.
Найти:
Дано:

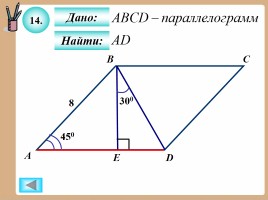
14.
Дано:
Найти:

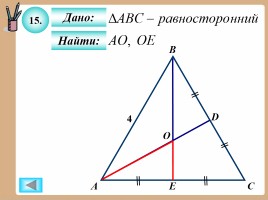
15.
Дано:
Найти:

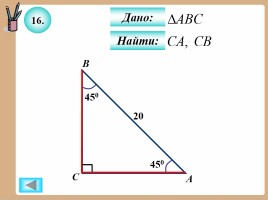
16.
Дано:
Найти:

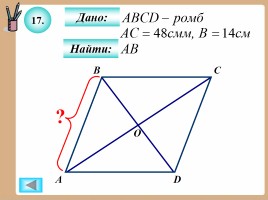
17.
Дано:
Найти:

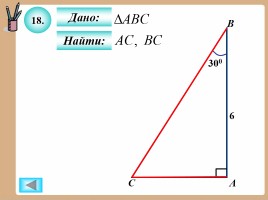
18.
Дано:
Найти:

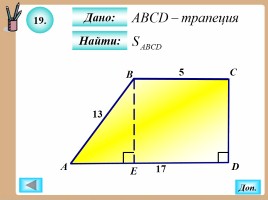
19.
Найти:
Дано:
B
C
D
13
5
17
А
Доп.
Е

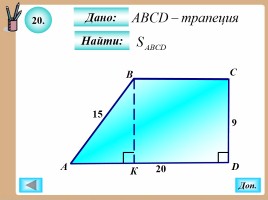
20.
Найти:
Дано:
B
C
D
15
9
20
А
К
Доп.

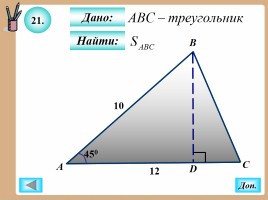
21.
Найти:
Дано:
А
B
C
D
450
Доп.
12
10

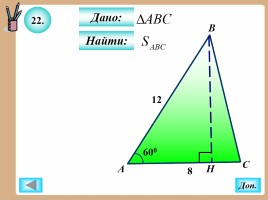
22.
Найти:
Дано:
А
B
C
Н
600
8
12
Доп.

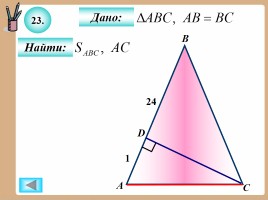
23.
Найти:
Дано:

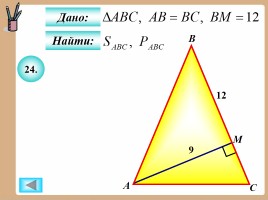
24.
Найти:
Дано:

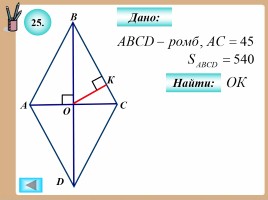
25.
Найти:
Дано:

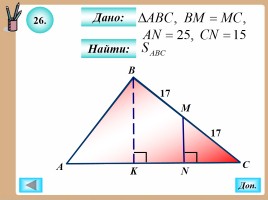
26.
Найти:
Дано:
А
B
C
М
K
17
N
Доп.
17

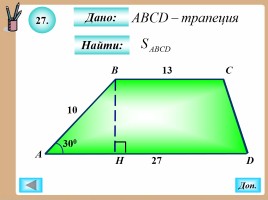
27.
Найти:
Дано:
А
B
C
D
H
27
13
10
300
Доп.

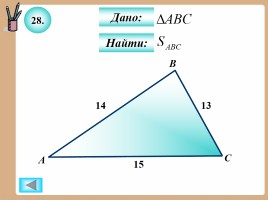
28.
Найти:
Дано:

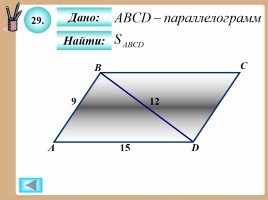
29.
Найти:
Дано:

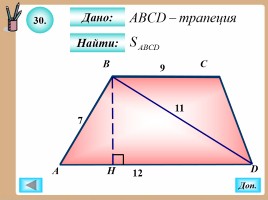
30.
Найти:
Дано:
А
B
C
D
H
11
7
9
12
Доп.

Вместо заключения
В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

1. Л.С. Атанасян. Геометрия 7-9 (учебник средней школы). - М., Просвещение, 2009 2. Г.И. Глейзер. История математики в школе. - М., Просвещение, 1964 3. Избранные вопросы математики (факультативный курс 7-8 кл.). - М., Просвещение, 1989 4. Л.Ф. Пичугин. За страницами учебника алгебры. - М., Просвещение, 1990 5. Энциклопедический словарь юного математика.- М., Просвещение, 1989 6. Я.И. Переман. Занимательная геометрия. – М., Наука, 1976
Использованная литература