Презентация - Объем прямой призмы

Объем прямой призмы

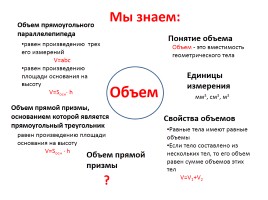
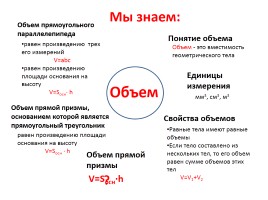
Объем
Понятие объема
Единицы измерения
Равные тела имеют равные объемы Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел V=V1+V2
равен произведению трех его измерений V=abc равен произведению площади основания на высоту V=Sосн· h
равен произведению площади основания на высоту V=Sосн · h
Объем прямой призмы
?
Объем - это вместимость геометрического тела
Свойства объемов
Объем прямой призмы, основанием которой является прямоугольный треугольник
Объем прямоугольного параллелепипеда
мм3, см3, м3
Мы знаем:

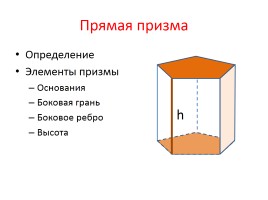
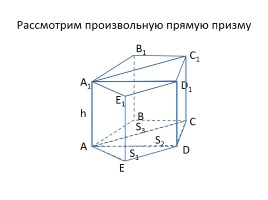
Прямая призма
Определение Элементы призмы Основания Боковая грань Боковое ребро Высота

h

Предположение
произведению площади основания на высоту
Объем прямой призмы равен ???

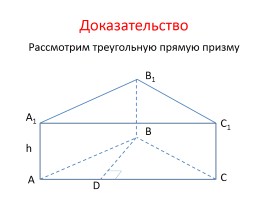
Рассмотрим треугольную прямую призму
Доказательство
D

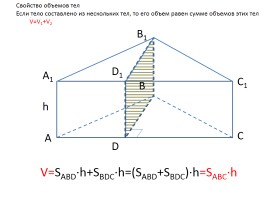
V=SABD·h+SBDC·h=(SABD+SBDC)·h=SABC·h
Свойство объемов тел Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел V=V1+V2

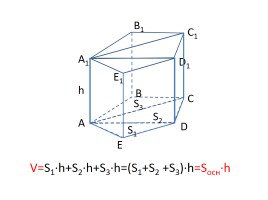
Рассмотрим произвольную прямую призму

V=S1·h+S2·h+S3·h=(S1+S2 +S3)·h=Sосн·h

Объём прямой призмы равен произведению площади основания на высоту

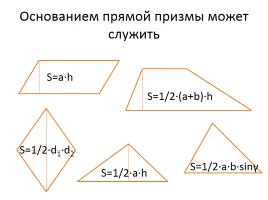
Основанием прямой призмы может служить
S=1/2·a·h
S=1/2·(a+b)·h
S=1/2·d1·d2
S=a·h
S=1/2·a·b·sinγ

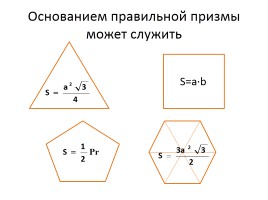
Основанием правильной призмы может служить
S=a·b

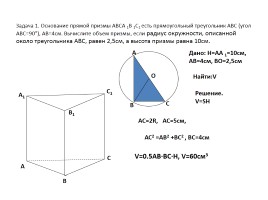
Задача 1. Основание прямой призмы АВСА 1В 1С1 есть прямоугольный треугольник АВС (угол АВС=90°), АВ=4см. Вычислите объем призмы, если радиус окружности, описанной около треугольника АВС, равен 2,5см, а высота призмы равна 10см.
о
А
В
С
А1
В1
С1
А
В
С
О
Дано: H=AA 1=10cм, АВ=4см, ВО=2,5см
Найти:V
Решение. V=SH
AC=2R, AC=5cм,
АС2 =АВ2 +ВС2 , ВС=4см
V=0.5AB∙BC∙H, V=60см3

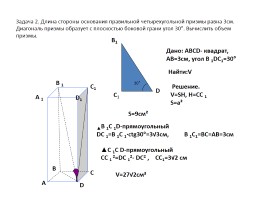
Задача 2. Длина стороны основания правильной четырехугольной призмы равна 3см. Диагональ призмы образует с плоскостью боковой грани угол 30°. Вычислить объем призмы.
А
В
С
D
A 1
B 1
C1
D1
C1
B1
D
30°
Дано: АВСD- квадрат, АВ=3см, угол В 1DC1=30°
Найти:V
Решение. V=SH, H=СС 1 S=a²
S=9cм²
▲В 1С 1D-прямоугольный DC 1=B 1C 1∙ctg30°=3√3см, В 1С1=ВС=АВ=3см
▲С 1С D-прямоугольный СC 1 2=DC 12- DC2 , СС1=3√2 см
V=27√2см3

Объем
Понятие объема
Единицы измерения
Равные тела имеют равные объемы Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел V=V1+V2
равен произведению трех его измерений V=abc равен произведению площади основания на высоту V=Sосн· h
равен произведению площади основания на высоту V=Sосн · h
Объем прямой призмы
?
Объем - это вместимость геометрического тела
Свойства объемов
Объем прямой призмы, основанием которой является прямоугольный треугольник
Объем прямоугольного параллелепипеда
мм3, см3, м3
Мы знаем:
V=Sосн·h

Домашнее задание
Теорема стр. 145 Базовый уровень № 663 Продвинутый уровень № 659
Успехов Вам!

Ппезентацию подготовила Вакилова В.В. учитель математики КОГОАУ «Многопрофильный лицей г.Вятские Поляны»

Используемая литература:
Л.С.Атанасян Геометрия 10-11 Интернет ресурсы- слайд 12, 13