Презентация - Квадратные уравнения

Квадратные уравнения
8 класс Обобщающий урок Разработала учитель математики МОУ ООШ №30 Гречишкина Н. Н.

Уравнения для меня важнее, потому что политика — для настоящего, а уравнения — для вечности. Альберт Эйнштейн Уравнение – это золотой ключ, открывающий все математические сезамы.» С. Коваль.

Цель урока:
Повторить основные способы решения квадратных уравнений. Провести исследовательскую работу, цель которой получить формулы , облегчающие решение квадратных уравнений

Устный опрос.
1)2х²-8х+4=0 2) 3х²+4х-1=0 3)4х²-8=0 4) х²-10х+100=0 5)5х²+6х=0 6) х²-7х+12=0 7) 3х²=0 8)14-2х² +х=0
1)Назовите номера полных квадратных уравнений. (1,2,4,6,8) 2) Какие уравнения называются квадратными? (Уравнения вида ах²+вх+с=0, где а≠0, а, в, с –некоторые числа, Х-неизвестное, называют квадратным уравнением) 3)Какие из этих уравнений приведённые? (4, 6,8) 4) Назовите коэффициенты в уравнении 8. (а=1, в=-2, с=14) 5)С чего лучше начать решение уравнения 1? ( Вынести множитель 2 ) 6) Назовите номера неполных квадратных уравнений. ( 3, 5, 7) 7) Какое из этих неполных уравнений имеет один корень? (7) 8) Назовите коэффициенты в уравнении 5. (а=5, в=6, с=0) 9) Найдите дискриминант в уравнении6. ( Д=в²-4ас=49-4*1*12=1) 10) Сколько корней имеет уравнение и какие? ( Два корня . Х1,2=(-в±√1)/2а; х1= 4, х2=3) 11) Найдите дискриминант в уравнении 4 и сделайте вывод о количестве корней .(Д= 10²-4*100˂0, значит корней нет) 12)Чему равна сумма и произведение корней в уравнении 6? ( 7 и 12)

Теорема Виета
Теорема. Если х1 и х2 – корни приведенного квадратного уравнения х2 + px + q = 0, то х1 + х2 = -р х1 ∙ х2 = q Корни х1 =3 и х2 = 4 в уравнении х2 - 7x +12 = 0. р = -7, q = 12. х1 + х2 = 3+4 = 7 = -р, х1 ∙ х2 = 3*4 = q.

Исторические сведения о Франсуа Виете (1540-1603)
Родился в 1540 году во Франции в Фонтене-ле-Конт. По профессии адвокат. В свободное время Виет занимается астрономией. Изучив ещё в молодости Коперникову систему мира, заинтересовался астрономией. Занятия астрономией требовали знания тригонометрии и алгебры. Виет занимался ими и вскоре пришёл к выводу, что необходимо усовершенствовать алгебру и тригонометрию, над чем и проработал ряд лет. Мы знаем, как легко решать квадратные уравнения. Для них существуют готовые формулы. До Франсуа Виета решение каждого квадратного уравнения выполнялось в виде очень длинных словесных рассуждений и описаний, довольно громоздких действий. Даже само уравнение в современном виде не могли записать. Для этого тоже требовалось довольно длинное и сложное словесное описание. На овладение приёмами решений уравнений требовались годы. Общих правил, подобных современным, не было, тем более формул решения уравнения. Постоянные коэффициенты буквами не обозначались. В 1591 году Виет ввёл буквенные обозначения и для неизвестных и для коэффициентов уравнения. Ввел формулы. После открытия Виета стало возможным записывать правила в виде формул.

Основные способы решения квадратных уравнений.Какое уравнение удобнее решать?
А 3х²-2х-5=0 Д х²=5 И 7х²+14х=0 Н х²+5х+4=0 О х²+4х+4=0 Т х²-4=0 Ф 2х²-11х+5=0 Е х²+2х=х²+6
1. Извлечением корней из обеих частей? Д 2.Вынесением общего множителя за скобки? И 3.Представляя его в виде квадрата двучлена. О 4. Используя общую формулу. Ф 5.По формуле, связанной с чётностью коэффициента. А 6.По теореме, обратной теореме Виета. Н 7.Разложением по формуле разности квадратов. Т

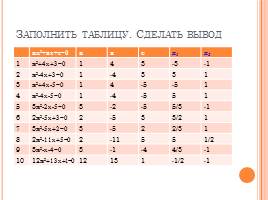
Заполнить таблицу. Сделать вывод
ах²+вх+с=0 а в с х1 х2
1 х²+4х+3=0 1 4 3 -3 -1
2 х²-4х+3=0 1 -4 3 3 1
3 х²+4х-5=0 1 4 -5 -5 1
4 х²-4х-5=0 1 -4 -5 5 1
5 3х²-2х-5=0 3 -2 -5 5/3 -1
6 2х²-5х+3=0 2 -5 3 3/2 1
7 3х²-5х+2=0 3 -5 2 2/3 1
8 2х²-11х+5=0 2 -11 5 5 1/2
9 3х²-х-4=0 3 -1 -4 4/3 -1
10 12х²+13х+1=0 12 13 1 -1/2 -1

Вывод:
Предположение : 1) Если в квадратном уравнении ах²+вх+с=0 а+в+с=0,то х1= 1 ,а х2= с/а Доказательство: Если а+в+с=0, то в=-(а+с). Д=(-(а+с)) ² - 4ас = а²+2ас +с²-4ас=а²-2ас+с²=(а-с) ². Д>0, то х2 = (а+с-√(а-с) ²)/2а=(а+с-а+с)/2а=2с/2а=с/ 2)Если а-в+с=0, то х1= - 1 , х2= - с/а

Самостоятельная работа.
1. Составить 5 уравнений , для решения которых применяются доказанные гипотезы. 2. Решить составленные уравнения. 3. Составить квадратное уравнение, корни которого равны 2+√3 и 2- √3.