Презентация - Многоугольники и их свойства

Многоугольники и их свойства
Полетаева Любовь Николаевна учитель математики МОУ Чамеровская средняя школа

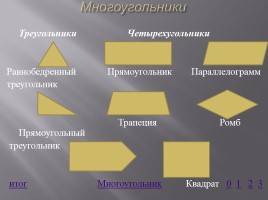
Многоугольники
Треугольники Четырехугольники Равнобедренный Прямоугольник Параллелограмм треугольник Трапеция Ромб Прямоугольный треугольник итог Многоугольник Квадрат 0 1 2 3

Равнобедренный треугольник
Три точки плоскости , соединенные между собой отрезками, называются треугольником. Равнобедренным называется такой треугольник , у которого две боковые стороны равны. Свойства: В равнобедренном треугольнике углы при основании равны. Задача

Прямоугольный треугольник
Три точки плоскости, соединенные между собой отрезками , называются треугольником. Прямоугольным называется треугольник , у которого один из углов прямой . Свойства: если один из углов прямоугольного треугольника равен 30°, то катет, лежащий против этого угла равен половине гипотенузы. Задача

Прямоугольник
Прямоугольником называется параллелограмм , у которого все углы прямые . Свойства : Сумма углов любого четырехугольника равна 360°. Диагонали прямоугольника равны, точкой пересечения делятся пополам . Противоположные углы попарно раны . Задача

Параллелограмм
Параллелограммом называется четырехугольник , у которого противоположные стороны попарно параллельны. Свойства : 1 В параллелограмме противоположные стороны равны и противоположные углы равны. 2 Диагонали параллелограмма точкой пересечения делятся пополам. Признаки: 1 Если в четырехугольнике две стороны равны и параллельны ,то этот четырехугольник – параллелограмм. 2 Если в четырехугольнике противоположные стороны попарно равны , то этот четырехугольник – параллелограмм. 3 Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам , то этот четырехугольник - параллелограмм . Задача .

Трапеция
Трапецией называется четырехугольник , у которого две стороны параллельны ,а две другие стороны не параллельны . 1 Трапеция называется равнобедренной , если ее боковые стороны равны . 2 Трапеция называется прямоугольной, если один из ее углов прямой. Задача

Ромб
Ромбом называется параллелограмм , у которого все стороны равны . Свойства: Диагонали ромба взаимно перпендикулярны , точкой пересечения делятся пополам и делят его углы пополам . Задача

Квадрат
Квадратом называется прямоугольник , у которого все стороны равны. 1 Все углы квадрата прямые . Диагонали квадрата равны , взаимно перпендикулярны , точкой пересечения делятся пополам и делят углы квадрата пополам. Задача

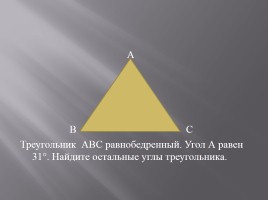
А В С Треугольник АВС равнобедренный. Угол А равен 31°. Найдите остальные углы треугольника.

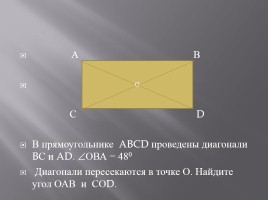
А В ОО С D В прямоугольнике ABCD проведены диагонали BС и AD. ОВА = 480 Диагонали пересекаются в точке О. Найдите угол ОАВ и СОD.
О

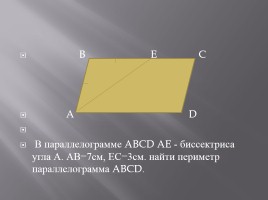
B E C A D В параллелограмме ABCD AE - биссектриса угла А. АВ=7см, ЕС=3см. найти периметр параллелограмма ABCD.

Трапеция
B C A E D В прямоугольной трапеции ABCD меньшая боковая сторона АВ = 10см, СDА = 450 , СЕ перпендикулярна АD. Найти DE.

C B D Ромб A Найдите углы, которые образуют диагонали ромба со стороной, если один из углов ромба равен 500

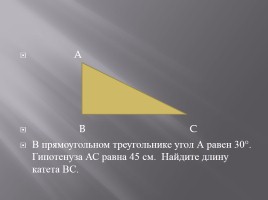
A B C В прямоугольном треугольнике угол А равен 30°. Гипотенуза АС равна 45 см. Найдите длину катета ВС.

многоугольник
Фигура, составленная из отрезков, не лежащих на одной прямой, называется многоугольником. Многоугольник является выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Свойства: сумма углов выпуклого n-угольника равна (n – 2) 180°. Задача.

Пятиугольник
Найдите сумму углов выпуклого пятиугольника.

Критерии оценки: Верно решено 9 заданий – «5» 7-8 заданий – «4» 6 заданий – «3» 3 задания и менее – «2»
№ 1 2 3 4 5 6 7 8 9
Вар-1 Б В Б В Б Б Б В В

Критерии оценки: Верно решено 9 заданий – «5» 7-8 заданий – «4» 6 заданий – «3» 3 задания и менее – «2»
№ 1 2 3 4 5 6 7 8 9
В- 2 В А А А А А А Б Б

1.Антонов Н. 2 3 3 2.Брусов С. 2 3 3 3.Долгова В. 2 4 3 4.Карпец А. 2 3 3 5.Комаров С 2 2 2 6.Пантелеева К. 3 4 4 7.Ратникова А. 2 3 3 8.Ригин К. 2 3 3 9.Умаров Г. 2 3 3 10.Шорникова В. 3 4 4

Оформление ответов на тест
№ 1 2 3 4 5 6 7 8 9
В -1