Презентация - Формулы сокращенного умножения
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 86%
- Слайдов: 51
- Просмотров: 5686
- Скачиваний: 2081
- Размер: 0.62 MB
- Класс: 7
- Формат: ppt / pptx
Примеры похожих презентаций
 Формулы сокращённого умножения 7 класс
Формулы сокращённого умножения 7 класс Формулы сокращенного умножения
Формулы сокращенного умножения Интерактивный плакат 7 класс «Формулы сокращённого умножения»
Интерактивный плакат 7 класс «Формулы сокращённого умножения» Формулы сокращенного умножения
Формулы сокращенного умножения Формулы сокращенного умножения
Формулы сокращенного умножения Урок обобщения знаний «Формулы сокращённого умножения»
Урок обобщения знаний «Формулы сокращённого умножения» Формулы сокращенного умножения (7 класс)
Формулы сокращенного умножения (7 класс)
Слайды и текст этой онлайн презентации
Слайд 1

ФОРМУЛЫ
СОКРАЩЕННОГО УМНОЖЕНИЯ
Класс 7 Учитель математики : Жиганова Екатерина Владимировна
2013 год
Байловский филиал Муниципального бюджетного общеобразовательного учреждения Пичаевской средней общеобразовательной школы
Слайд 2

Цели:
Познакомиться с формулами сокращенного умножения: квадрат суммы квадрат разности разность квадратов Рассмотреть геометрический смысл формул сокращенного умножения. Закрепить полученные знания в ходе выполнения заданий
2 из 56
Познакомиться с формулами сокращенного умножения: квадрат суммы квадрат разности разность квадратов Рассмотреть геометрический смысл формул сокращенного умножения. Закрепить полученные знания в ходе выполнения заданий
2 из 56
Слайд 3

Вы знаете, что при умножении многочлена на многочлен каждый член одного многочлена умножается на каждый член другого.
Но в некоторых случаях умножение многочленов можно выполнить короче.
3 из 56
3 из 56
Слайд 4

Для этого нужно воспользоваться
Формулами сокращённого умножения
4 из 56
Слайд 5

КВАДРАТ
СУММЫ
5 из 56
5 из 56
Слайд 6
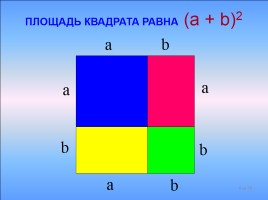
a b
a
b
a
b
a
b
ПЛОЩАДЬ КВАДРАТА РАВНА (a + b)2
6 из 56
a
b
a
b
a
b
ПЛОЩАДЬ КВАДРАТА РАВНА (a + b)2
6 из 56
Слайд 7
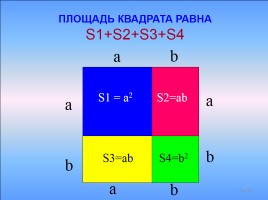
S1 = a2
S2=ab
S3=ab
S4=b2
ПЛОЩАДЬ КВАДРАТА РАВНА S1+S2+S3+S4
a
b
a
b
b
a
b
a
7 из 56
S2=ab
S3=ab
S4=b2
ПЛОЩАДЬ КВАДРАТА РАВНА S1+S2+S3+S4
a
b
a
b
b
a
b
a
7 из 56
Слайд 8
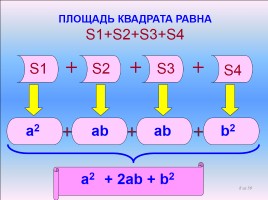
ПЛОЩАДЬ КВАДРАТА РАВНА S1+S2+S3+S4
S2
S3
S4
S1
+
+
+
а2
ab
ab
b2
а2 + 2ab + b2
+
+
+
8 из 56
S2
S3
S4
S1
+
+
+
а2
ab
ab
b2
а2 + 2ab + b2
+
+
+
8 из 56
Слайд 9

Выразили одну и ту же площадь двумя способами
S = (a+b)2 S = a2 + 2ab + b2
9 из 56
S = (a+b)2 S = a2 + 2ab + b2
9 из 56
Слайд 10

(a+b)2 = a2 +2ab + b2
ПОЛУЧИЛИ
10 из 56
Слайд 11

Полученное тождество
Формулой квадрата суммы
(a+b)2 = a2 +2ab + b2
называется
11 из 56
Слайд 12

Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого на второе, плюс квадрат второго выражения.
(a+b)2 = a2 +2ab + b2
12 из 56
Слайд 13

применения формулы квадрата суммы
Пример
Раскройте скобки в выражении (3x + 4ky)2
13 из 56
Слайд 14

применения формулы квадрата суммы
2
•
•
+
2
+
2
+
2
=
3х
4kу
3x
3x
4kу
4kу
Пример
14 из 56
Слайд 15

применения формулы квадрата суммы
= 9x 2 +24xky + 16k2y2
+
2
=
3х
4kу
Пример
15 из 56
Слайд 16

Возведем в квадрат сумму 7n + 4m
По формуле квадрата суммы получим: (7n + 4m)2 = = (7n)2 + 2 7n 4m + (4m)2 = = 49n2 + 56nm + 16m2
16 из 56
По формуле квадрата суммы получим: (7n + 4m)2 = = (7n)2 + 2 7n 4m + (4m)2 = = 49n2 + 56nm + 16m2
16 из 56
Слайд 17

Раскройте скобки в выражениях
1) (3 + 8р)2 2) ( 6х + 4)2 3) (4,2 + 0,5х)2 4) (0,3ху+k)2
17 из 56
= 64р2 + 48р + 9
= 36х2 + 48х + 16
= 0,25х2+4,2х+17,64
=0,09х2у2+0,6хуk+k2
1) (3 + 8р)2 2) ( 6х + 4)2 3) (4,2 + 0,5х)2 4) (0,3ху+k)2
17 из 56
= 64р2 + 48р + 9
= 36х2 + 48х + 16
= 0,25х2+4,2х+17,64
=0,09х2у2+0,6хуk+k2
Слайд 18

КВАДРАТ
РАЗНОСТИ
18 из 56
18 из 56
Слайд 19

Возведем в квадрат разность a - b
(a – b) = = (a – b)(a – b) = … Закончите преобразование
19 из 56
2
(a – b) = = (a – b)(a – b) = … Закончите преобразование
19 из 56
2
Слайд 20

Проверьте результаты преобразований
(a – b) = = a – 2ab + b
20 из 56
2
2
2
(a – b) = = a – 2ab + b
20 из 56
2
2
2
Слайд 21

Полученное тождество
Формулой квадрата разности
(a – b)2 = a2 – 2ab + b2
называется
21 из 56
Слайд 22

Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого на второе, плюс квадрат второго выражения.
(a - b)2 = a2 - 2ab + b2
22 из 56
Слайд 23

применения формулы квадрата разности
Раскройте скобки в выражении (5pn – 2m)2
Пример
23 из 56
Слайд 24

применения формулы квадрата разности
Пример
2
•
•
2
+
2
2
=
5pn
2m
5pn
5pn
2m
2m
24 из 56
Слайд 25

применения формулы квадрата разности
Пример
= 25p2n2 - 20pnm + 4m2
2
=
5pn
2m
25 из 56
Слайд 26

Возведем в квадрат разность 7х – 4у
По формуле квадрата разности получим: (7х – 4у)2 = = (7х)2 - 2 7х 4у + (4у)2 = = 49х2 - 56ху + 16у2
26 из 56
По формуле квадрата разности получим: (7х – 4у)2 = = (7х)2 - 2 7х 4у + (4у)2 = = 49х2 - 56ху + 16у2
26 из 56
Слайд 27

Раскройте скобки в выражениях
1) (5х-3)2 2) (13-6р)2 3) (2,3-0,4х)2 4) (0,6ху-k)2
27 из 56
=25х2 – 30х + 9
=36р2–156р+169
=0,16х2–1,84х+5,29
=0,36х2у2–1,2хуk+k2
1) (5х-3)2 2) (13-6р)2 3) (2,3-0,4х)2 4) (0,6ху-k)2
27 из 56
=25х2 – 30х + 9
=36р2–156р+169
=0,16х2–1,84х+5,29
=0,36х2у2–1,2хуk+k2
Слайд 28

РАЗНОСТЬ
КВАДРАТОВ
28 из 56
28 из 56
Слайд 29
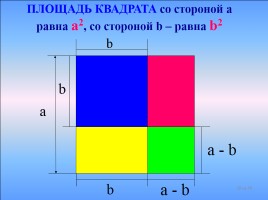
b
b
b
a - b
a - b
a
ПЛОЩАДЬ КВАДРАТА со стороной а равна а2, со стороной b – равна b2
29 из 56
b
b
a - b
a - b
a
ПЛОЩАДЬ КВАДРАТА со стороной а равна а2, со стороной b – равна b2
29 из 56
Слайд 30
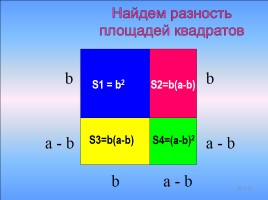
S1 = b2
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
b
a - b
b
a - b
a - b
b
Найдем разность площадей квадратов
30 из 56
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
b
a - b
b
a - b
a - b
b
Найдем разность площадей квадратов
30 из 56
Слайд 31
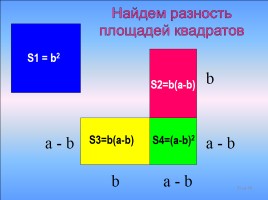
S1 = b2
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
a - b
b
a - b
a - b
b
Найдем разность площадей квадратов
31 из 56
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
a - b
b
a - b
a - b
b
Найдем разность площадей квадратов
31 из 56
Слайд 32
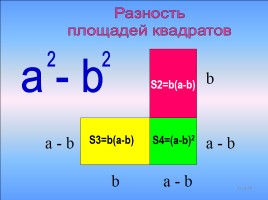
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
a - b
b
a - b
a - b
b
Разность площадей квадратов
а - b
2
2
а - b
32 из 56
S3=b(a-b)
S4=(a-b)2
a - b
b
a - b
a - b
b
Разность площадей квадратов
а - b
2
2
а - b
32 из 56
Слайд 33

a2 – b2 = S2 + S3 + S4
S2 = b(a – b) S3 = b(a – b) S4 = (a – b)2
33 из 56
S2 = b(a – b) S3 = b(a – b) S4 = (a – b)2
33 из 56
Слайд 34
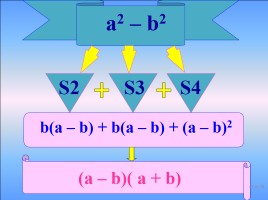
a2 – b2
S2
S3
S4
+
+
(a – b)( a + b)
b(a – b) + b(a – b) + (a – b)2
34 из 56
Слайд 35

a2 – b2 = (a – b)(a + b)
ПОЛУЧИЛИ
35 из 56
Слайд 36

Полученное тождество
Формулой разности квадратов
a2 – b2 = (a – b)(a + b)
называется
36 из 56
Слайд 37

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 – b2 = (a – b)(a + b)
37 из 56
Слайд 38

применения формулы разности квадратов
Пример
Разложите на множители выражение 25x2 - 4y2
38 из 56
Слайд 39

применения формулы разности квадратов
+
2
=
5х
2у
5x
5x
2у
2у
2
Пример
39 из 56
Слайд 40

= (5x – 2у)(5х + 2у)
2
=
5х
2у
2
Пример
применения формулы разности квадратов
40 из 56
Слайд 41

Разложите на множители выражение 49n2 - 4m2
По формуле разности квадратов получим: 49n2 - 4m2 = = (7n)2 - (2m)2 = = (7n – 2m)(7n + 2m)
41 из 56
По формуле разности квадратов получим: 49n2 - 4m2 = = (7n)2 - (2m)2 = = (7n – 2m)(7n + 2m)
41 из 56
Слайд 42

Разложите на множители выражения
1) 9-16р2 2) 36х2-64
42из 56
=(3 – 4p)(3 + 4p)
=(6x – 8)(6x + 8)
1) 9-16р2 2) 36х2-64
42из 56
=(3 – 4p)(3 + 4p)
=(6x – 8)(6x + 8)
Слайд 43

Попробуйте разложить на множители следующее выражение
16х8 – 9
43 из 56
Подсказка :
16х8 = (4х4)2
16х8 – 9
43 из 56
Подсказка :
16х8 = (4х4)2
Слайд 44

16х8 – 9=
= (4х4 – 3)(4х4 + 3)
Проверьте свои результаты
44 из 56
Проверьте свои результаты
44 из 56
Слайд 45

Поменяем местами правую и левую части в формуле разности квадратов.
получим:
(a – b)(a + b) = a2 – b2
45 из 56
получим:
(a – b)(a + b) = a2 – b2
45 из 56
Слайд 46

Это тождество позволяет сокращенно выполнять умножение разности любых двух выражений на их сумму.
(a – b)(a + b) = a2 – b2
46 из 56
Слайд 47

Выполните умножение выражений
47 из 56
(k–c)(k+c) (4f+3)(4f–3) (5d–7b)(5d+7b)
= k2 – c2
= 25d2– 49b2
= 16f 2– 9
47 из 56
(k–c)(k+c) (4f+3)(4f–3) (5d–7b)(5d+7b)
= k2 – c2
= 25d2– 49b2
= 16f 2– 9
Слайд 48

Самое главное:
Формула квадрата суммы: (a+b)2 = a2 +2ab + b2 Формула квадрата разности: (a - b)2 = a2 - 2ab + b2 Формула разности квадратов: a2 – b2 = (a – b)(a + b)
48 из 56
Формула квадрата суммы: (a+b)2 = a2 +2ab + b2 Формула квадрата разности: (a - b)2 = a2 - 2ab + b2 Формула разности квадратов: a2 – b2 = (a – b)(a + b)
48 из 56
Слайд 49

Закрепление материала
№ 33.1 № 33.4 № 33.14 № 33.18 (а, б) № 33.20 № 33.23
49 из 56
№ 33.1 № 33.4 № 33.14 № 33.18 (а, б) № 33.20 № 33.23
49 из 56
Слайд 50

Ответим на вопросы:
1) Для чего нужны формулы сокращённого умножения? 2) Сформулируйте формулу квадрата суммы. 3) Запишите формулу квадрата суммы. 4) Сформулируйте формулу квадрата разности. 5) Запишите формулу квадрата разности. 6) Сформулируйте формулу разности квадратов. 7) Запишите формулу разности квадратов.
50 из 56
1) Для чего нужны формулы сокращённого умножения? 2) Сформулируйте формулу квадрата суммы. 3) Запишите формулу квадрата суммы. 4) Сформулируйте формулу квадрата разности. 5) Запишите формулу квадрата разности. 6) Сформулируйте формулу разности квадратов. 7) Запишите формулу разности квадратов.
50 из 56
Слайд 51

Используемая литература:
1) Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 класса общеобразовательных учреждений. – М.: Просвещение, 2008. 2) Учебное издание «Программы общеобразовательных учреждений: Алгебра. 7-9 кл.»/ Сост. Т.А.Бурмистрова. – 2-е изд.– М. Просвещение, 2009. 3) Мартышова Л.И. Контрольно-измерительные материалы. Алгебра: 7 класс. – М.: ВАКО, 2010.
51 из 56
1) Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 класса общеобразовательных учреждений. – М.: Просвещение, 2008. 2) Учебное издание «Программы общеобразовательных учреждений: Алгебра. 7-9 кл.»/ Сост. Т.А.Бурмистрова. – 2-е изд.– М. Просвещение, 2009. 3) Мартышова Л.И. Контрольно-измерительные материалы. Алгебра: 7 класс. – М.: ВАКО, 2010.
51 из 56
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
