Презентация - Модуль действительного числа

Модуль действительного числа
Автор материала: Дудниченко Татьяна Анатольевна, учитель математики
 первой квалификационной категории ГАОУ СОШ МГПУ, г. Москва

Цели и задачи урока
Ввести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля; Ввести функцию y = |x|, показать правила построения ее графика; Научить разными способами решать уравнения, содержащие модуль; Развивать интерес к математике, самостоятельность, логическое мышление, математическую речь, прививать аккуратность и трудолюбие.

Определение.
Например: |8|=8; |-8|=-(-8)=8;

Свойства модуля

Геометрический смысл модуля
Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две точки a и b и постараемся найти расстояние ρ(a;b) между этими точками. Очевидно что это расстояние равно b-a, если b>a Если поменять местами, то есть a>b, расстояние будет равно a-b. Если a=b то расстояние равно нулю, так как получается точка. Все три случая мы можем описать единообразно:

Пример. Решите уравнение: а) |x-3|=6 б) |x+5|=3 в) |x|=2.8 г) Решение. а) Нам нужно найти на координатной прямой такие точки, которые удалены от точки 3 на расстояние равное 6. Такие точки 9 и -3. (Прибавили и отняли шестерку от тройки.) Ответ: х=9 и х=-3 б) |x+5|=3, перепишем уравнение в виде |x-(-5)|=3. Найдем расстояние от точки -5 удаленное на 3. Такое расстояние, получается, от двух точек: х=2 и х=-8 Ответ: х=2 и х=-8. в) |x|=2.8, можно представить в виде |х-0|=2.8 или Очевидно, что х=-2.8 или х=2.8 Ответ: х=-2.8 и х=2.8. г) эквивалентно Очевидно, что

Функция y = |x|

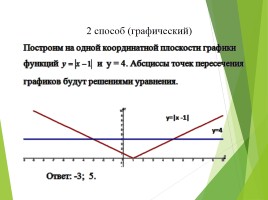
Решить уравнение |x-1| = 4
1 способ (аналитический)
Задание 2

2 способ (графический)

3 способ

Модуль действительного числа.
Тождество Рассмотрим выражение , если а>0, то мы знаем что . Но как быть, в случае если a<0? Ведь не может быть , в таком случае корень равен отрицательному числу. Давайте рассмотрим –а. 1. Если а<0 то –а>0. 2. Давайте обобщим: По определению модуля: То есть

Модуль действительного числа.
Пример. Упростить выражение если: а) а-2≥0 б) a-2<0 Решение. Справедливо тождество: а) Если а-2≥0, то |a-2|=a-2. Таким образом получаем б) Если а-2<0, то |a-2|=-(a-2)=2-a. Таким образом получаем

Модуль действительного числа.
Пример. Вычислить Решение. Мы знаем что: Осталось раскрыть модули Рассмотрим первое выражение:

Рассмотрим второе выражение: Используя определение раскроем знаки модулей: В итоге получили: Ответ: 1.

Закрепление нового материала.
№ 16.2, №16.3, №16.4, №16.12, №16.16 ( а, г), №16.19

Задачи для самостоятельного решения. 1. Решите уравнение: а) |x-10|=3 б) |x+2|=1 в) |x|=2.8 г) 2. Решить уравнение: а) |3x-9|=33 б)|8-4x|=16 в)|x+7|=-3 3. Упростить выражение если а) а-3≥0 б) a-3<0 4. Вычислите
Задачи для самостоятельного решения
Домашнее задание: прочитать материал §16, №16.6 16.11, 16.22

Список использованной литературы: Звавич Л.И. Алгебра. Углубленное изучение. 8 кл.: задачник / Л.И. Звавич, А.Р. Рязановский. – 4-е изд., испр. – М.: Мнемозина, 2006. – 284 с. Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович. – 12-е изд., стер. – М.: Мнемозина, 2014. – 215 с. Мордкович А.Г и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 12-е изд., испр. и доп. – М.: Мнемозина, 2014. – 271 с.