Презентация - Понятие вектора

Понятие вектора
Л.С. Атанасян "Геометрия 7-9"

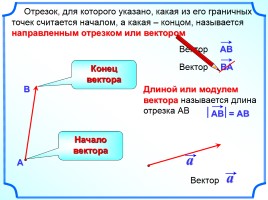
Длиной или модулем вектора называется длина отрезка АВ
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором
Начало вектора
Конец вектора

Любая точка плоскости также является вектором. В этом случае вектор называется нулевым
Длина нулевого считается равной нулю
Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора.

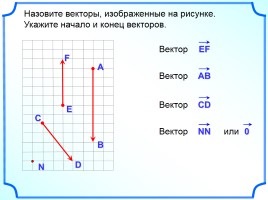
Назовите векторы, изображенные на рисунке. Укажите начало и конец векторов.

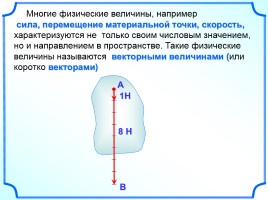
Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (или коротко векторами)
8 Н

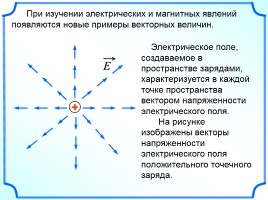
При изучении электрических и магнитных явлений появляются новые примеры векторных величин.

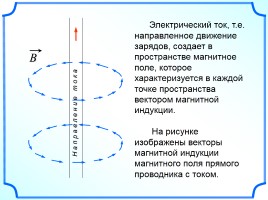
Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции. На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.

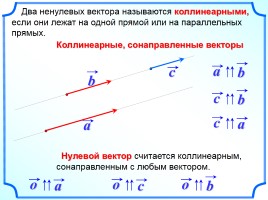
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Коллинеарные, сонаправленные векторы
Нулевой вектор считается коллинеарным, сонаправленным с любым вектором.

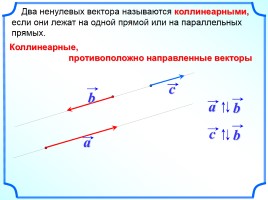
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Коллинеарные, противоположно направленные векторы

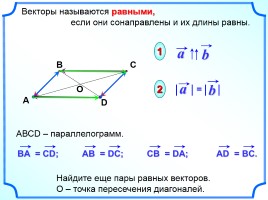
Векторы называются равными, если они сонаправлены и их длины равны.
1
2
Найдите еще пары равных векторов. О – точка пересечения диагоналей.

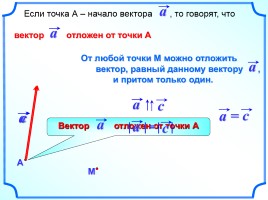
Если точка А – начало вектора , то говорят, что вектор отложен от точки А

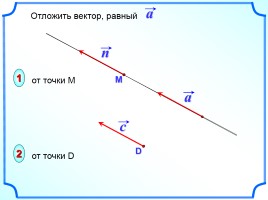
1
2
от точки М
от точки D

С
А
В
D
4
3
4
3
1,5
4
5
5
M
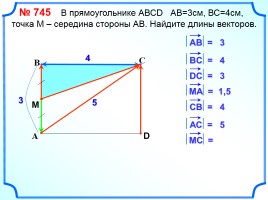
№ 745 В прямоугольнике АВСD АВ=3см, ВС=4см, точка М – середина стороны АВ. Найдите длины векторов.

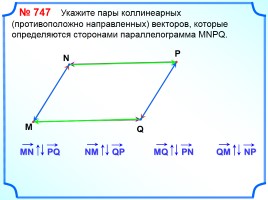
№ 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами параллелограмма MNPQ.
M
N
P
Q

№ 747 Укажите пары коллинеарных (противоположно направленных) векторов, которые определяются сторонами параллелограмма MNPQ.
M
N
P
Q

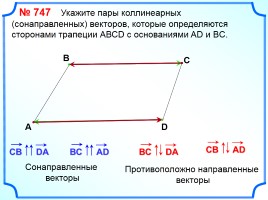
№ 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами трапеции АВСD с основаниями AD и BC.
А
В
С
D
Сонаправленные векторы
Противоположно направленные векторы

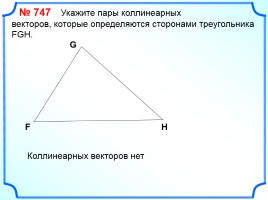
№ 747 Укажите пары коллинеарных векторов, которые определяются сторонами треугольника FGH.
F
G
H
Коллинеарных векторов нет

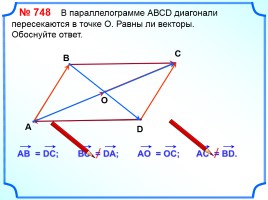
№ 748 В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы. Обоснуйте ответ.
А
В
С
D

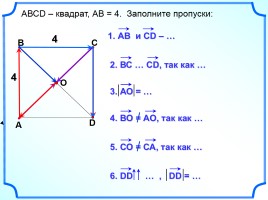
АВСD – квадрат, АВ = 4. Заполните пропуски:
4
4

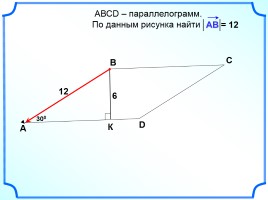
АВСD – параллелограмм. По данным рисунка найти
А
В
С
D
300
6
К
12
= 12

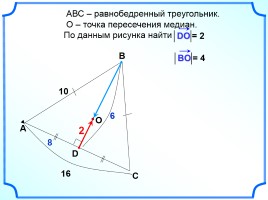
АВС – равнобедренный треугольник. О – точка пересечения медиан. По данным рисунка найти
А
В
С
10
= 2
8
2
= 4

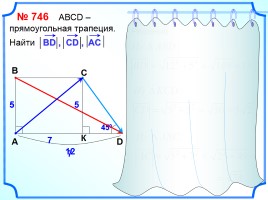
№ 746 АВСD – прямоугольная трапеция. Найти
A
B
C
D
12
5
450
Решение
5
5
7
7

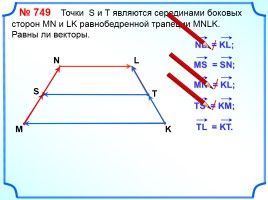
№ 749 Точки S и Т являются серединами боковых сторон MN и LK равнобедренной трапеции MNLK. Равны ли векторы.
M
N
L
K
S
T

а) коллинеарные векторы; б) сонаправленные векторы; в) противоположные векторы; г) равные векторы; д) векторы, имеющие равные длины.
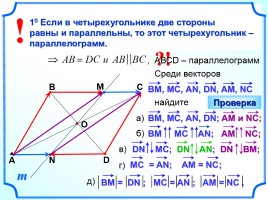
В четырехугольнике АВСD , О – точка пересечения диагоналей. Прямая проходит через точку О и пересекает стороны ВС и АD в точках М и N соответственно.
А
В
С
D
m
?!
Среди векторов найдите
, АВСD – параллелограмм
Проверка