Презентация - Приёмы быстрого устного счёта: метод или гениальность?

Приёмы быстрого устного счёта: метод или гениальность?
А. Галстян, рук. Л. Д. Жингалова МАОУ гимназия им. Н. В. Пушкова

1. Актуальность темы и цели исследования 3. Феноменальные счетчики 4. Способы быстрого счета 5. Исследование эффективности способов быстрого счета 6. Счетчики-спортсмены 7. Выводы
план

В начальной школе очень большую часть учебного времени мы тратили на развитие навыков устного счета. Да и сейчас, в пятом классе, мы посвящаем этому время практически каждый день. А ведь мы могли это время потратить на что-то другое! Потому что: У нас есть компьютеры Даже в мобильном телефоне встроен калькулятор Человек не может обогнать компьютер по скорости счета Так зачем же мы тратим время на устный счет?
нужно ли быстро считать в уме

Выяснить, можно ли научить любого быстрому счету или это врожденная способность, которая либо есть у человека, либо ее нет.
Цель работы

существуют ли люди, действительно быстро считающие, и что значит «действительно быстро»? как эти люди достигли такой скорости счета? как им пригодилось это умение в жизни? можно ли научить быстро считать любого? стоит ли учиться быстро считать?
Для достижения цели работы нам нужно выяснить

Феноменальный счётчик (устар.), супервычислитель (совр.)  — человек, обладающий способностью к быстрому счёту, выполняемому с помощью математических алгоритмов исключительно на основе визуальных представлений без произнесения слов о выполняемых действиях и полученных результатах
гениальность?

Альфред Бине выделил общие отличительные черты феноменальных счетчиков: отсутствие влияний наследственности и среды, принадлежность по происхождению к бедной неимущей среде; очень раннее и всегда предшествующее обучению чтению и письму обнаружение счётной способности (в среднем в возрасте 8 лет); поглощение умственной деятельности упражнениями в действиях над числами; дальнейшее развитие счётной способности при упражнении и быстрый её упадок в случаях неиспользования
гениальность?

Чтобы проверить эффективность некоторых способов быстрого счета, мы провели тестирование в двух пятых классах В рамках этого теста мы дали ученикам 8 примеров и зафиксировали лучший, худший и средний результат по скорости решения Затем мы ознакомили учеников со способами быстрого счета, применимыми к таким примерам, и дали решить еще по 8 аналогичных примеров уже с использованием этих приемов
исследование эффективности

Примеры после объяснения: 676:4= 472:4= 900:5 1200:5 314*9 274*9 14*13 15*14
исследование эффективности
Примеры после объяснения: 676:4= 472:4= 900:5 1200:5 314*9 274*9 14*13 15*14

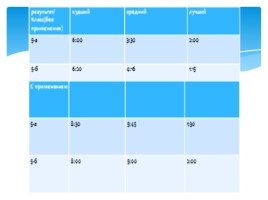
результат/ Класс(без применения) худший средний лучший
5-а 6:00 3:30 2:00
5-б 6:20 4:16 1:15
С применением
5-а 8:30 5:45 1:30
5-б 8:00 5:00 2:00

Применение приёмов быстрого счёта позволило улучшить лучший результат, но ухудшило худший. Худший и средний результаты с использованием приемов быстрого счета были хуже, чем без их использования. Следовательно, приемы быстрого счета могут помочь только при условии тренировок в их применении, и они лучше и быстрее помогают тем, кто и без них имел хорошие способности к счету
В результате эксперимента выяснено:

Приёмы быстрого счёта – не гениальность. И быстрый счёт – не гениальность. Быстрый счёт – полезная способность, которая не гарантирует успеха, но может пригодиться в жизни. Приёмы быстрого счёта – упражнения позволяющие развить данную способность. Они как физкультура: чемпионом не сделают, но поддерживают в форме.
вывод

Да – как минимум чтобы рассчитать тормозной путь, когда несёшься на своей «Феррари» со скоростью 200 км/ч. Калькулятор там не поможет.
Нужно ли уметь быстро считать в уме?

Спасибо за внимание!

1.феноменальные счётчики 2.способы быстрого счёта 3.счётчики-спортсмены
Вспомогательные слайды

феноменальные счетчики
Люди-калькуляторы (mental calculators)

Зера Колберн (1804-1840), шт. Вермонт, США: В 6 лет - умножил в уме 12 225 на 1223. Отец Зеры эксплуатировал талант сына, не давая ему толком учиться. В результате к моменту смерти отца (1822 год) способности Зеры к быстрым вычислениям угасли, он стал обычным человеком, хотя и выше среднего уровня. В 18 лет - стал учителем математики в школе, параллельно поступив учиться на священника. В 31 год - стал профессором лингвистики.
гениальность?

Луи Флери (1893-1980, Франция), слепой от рождения: 10 лет – не может одеваться, плохо ходит, не поддается обучению (в том числе элементарной арифметике) 15 лет – помещен в клинику для неизлечимо больных, где вскоре перенес сильный шок, увидев припадок другого больного. После перенесенного шока стал проявлять поразительные способности в устном счете, а также его мыслительная деятельность в целом нормализовалась 34 года - за 2 с умножал З-значное число на 2-значное и за 10с З-значное на З-значное
гениальность?

Иоган Захариас Дазе (1824-1861, Германия) С 3 лет – способности к арифметическим вычислениям 15 лет – выступает с демонстрацией своих способностей в разных городах К 26 годам так и не освоил даже в минимальной степени ни одного иностранного языка, и даже элементарных концепций классической математики В 1849 году он предложил Гамбургской академии наук составить таблицу факторов (возможных делителей) для всех чисел от 7 миллионов до 10 миллионов, и получил грант на эту работу К моменту свой смерти Дазе составил эту таблицу для чисел между 7 и 8 миллионами, а также почти полностью следующий миллион
Гениальность?

Карл Фридрих Гаусс (1777-1855, Германия) 3 года – наблюдал за расчетами отца с работниками, и нашел ошибку в вычислениях. 7 лет – быстрее всех решал примеры в школе. 1798-1808 гг. – десятилетие творчества и великих открытий: решил ряд задач, не поддававшихся другим ученым многие годы и даже тысячелетия; вычислил и указал место нахождения малой планеты – Цереры 30 лет – получает кафедру математики и астрономии в Геттингенском университете, а затем должность директора Геттингенской астрономической обсерватории До конца жизни занимался исследованиями и достиг потрясающих результатов в области алгебры, геометрии, физики и астрономии
Гениальность?

Андре Мари Ампер (1775-1836, Франция) Получил домашнее образование – вообще не посещал школу 4 года – делает длинные вычисления в уме, пользуясь правилами, которые узнал из игр в камешки 13 лет – направил в Лондонскую академию наук несколько мемуаров по математике, в том числе серьезные замечания по трудам всемирно известного математика Эйлера Был наделен феноменальной памятью и способностью у устному счету, но никогда не занимался развитием именно вычислительных способностей 1820 год – сделал сообщения об электромагнетизме, за которые его называют «Ньютоном электричества»
Гениальность?

Герт Митринг (р. 1966, Германия) 4 года – в магазине, пока его мать складывала в корзинку выбранный товар, сообщил ей, сколько нужно будет за всё заплатить 12 лет - создал математические формулы, с помощью которых можно было установить, какой день недели соответствует той или иной дате на протяжении минувших четырёх тысяч лет 38 лет – извлек за 11,8 с корень 13-й степени из числа ниже: 706643738116724861022340088302401573757042331170702632731269721516000395709065419973141915549389684111 Написал несколько книг о приемах быстрого счета К 2004 году защитил две докторские диссертации – в области математики и психологии
Гениальность?

Приемы быстрого счета

1. Умножение в пределах от 10 до 20: к одному из чисел прибавляем количество единиц другого, сумму умножаем на 10 и прибавляем произведение единиц чисел. Пример: 13*12=(13+2)*10+3*2=156
Умножение НАТУРАЛЬНЫХ чисел

Умножение на 9 Приписать 0 и отнять исходное число Пример: 241*9=2410-241=2169
Умножение НАТУРАЛЬНЫХ чисел

Герт Митринг разработал умножение на пальцах в пределах ста. Он предлагает брать за основу круглое двухзначное число и изображать единицы: пальцы вверх – нормальное число; пальцы вниз – отрицательное. Например: 33х33 Шаг 1: изобразить число 33. За основу берем 30 (т.к. это ближайшее число целых десятков). На руках выставляем по 3 пальца вверх. Шаг 2: возводим в квадрат число 30. 30х30=900 К этому числу прибавляем по 30 за каждый палец, и получаем промежуточный результат: 30х30+30х6=1080 В заключение, прибавляем к промежуточному результату малый результат (3х3=9), и получаем итог: 1080+9=1089
Умножение на пальцах

1. Деление на 5,50,25: удобно помнить, что: X : 5 = X*2:10 X : 50= X*2:100 X : 25 = X*4:100 Пример: 125:5=125*2:10=25 2. Деление на 4,8: удобно помнить, что: А:2:2=А:4 А:4:2=А:8
деление НАТУРАЛЬНЫХ чисел

Чемпионат Мира по устным вычислениям 2014 прошел 10/10/2014 - 12/10/2014 iна факультете математики в Дрезденском Университете Технологии в Германии. 39участников из 17 стран 5 основных видов состязаний: Сложение десяти 10-значных чисел, 10 задач за 7 минут Победитель: Granth Thakkar (Индия); 10 правильных результатов за 242 секунды Умножение двух 8-значных чисел, 10 задач за 10 минут Победитель: Marc Jornet Sanz (Испания)), 10 правильных результатов за 295 секунд Вычисления календарных дат, 1 минута, даты вразброс за годы 600–2100 Победитель: Marc Jornet Sanz (Испания), 64 правильных результата Квадратные корни из 6-значных чисел, 10 задач за 10 минут Победитель: Rhea Shah (IИндия), 10 правильных результатов за135 seconds (каждый ответ вычислен до восьми знаков) Самый универсальный вычислитель (лучший счет за решение 5 заранее не объявленных типов задач) Победитель: Andreas Berger (Германия), 365/500 .
Чемпионат мира по устному счёту