Презентация - Определитель и его свойства" для 11 класса

Тема: «Определитель и его свойства».
Даниленко Светлана Владимировна, преподаватель естественнонаучных дисциплин КГБОУ СПО Хабаровский Промышленно- Экономический Техникум
Конкурс интерактивных презентаций "Интерактивная мозаика" «Сообщество взаимопомощи учителей Pedsovet.su»

Тема: «Определитель и его свойства».
Ход занятия 1. Контроль исходного уровня знаний по теме: «Матрица». 2. Объяснение нового материала. а) Вычисление определителей 2-го порядка. б) Вычисление определителей 3-го порядка. в) Основные свойства определителя. г) Теорема о разложении определителя по элементам строки или столбца. 3. Закрепление нового материала. 4. Домашнее задание.
Цель: 1. Изучить свойства определителей и способы их вычисления. 2. Научиться производить расчёты определителей разными способами (подготовиться к практической работе).

Контроль исходного уровня знаний по теме: "Матрица"
Выберите любую букву из данного слова и выполните задание:
М А Т Р И Ц А

Сформулируйте определение матрицы
Проверь себя!

Определение:
Матрицей размером m  n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

А ну-ка, умножь матрицу на число!
Найди ошибку в умножении матрицы А на 5:

МОЛОДЕЦ!!!

Транспонирование матрицы
Найдите ошибку в транспонированной матрице Аt:


МОЛОДЕЦ!!!

Разность двух матриц
Сформулируйте операцию вычитания двух матриц одинаковой размерности.
Проверь себя!

Определение:
Разностью двух матриц А и В одинаковой размерности, называется матрица: А-В=А+(-1)·В

И какие же ты, знаешь виды матриц?
Проверь себя!

Виды матриц

Найти ошибку при сложении матриц А и В:
Цифровое значение суммы матриц

МОЛОДЕЦ!!!

Арифметическая ошибка при умножении матриц
Найдите произведение матрицы А на В и исправьте ошибку:

МОЛОДЕЦ!!!

Определение:
можно поставить в соответствие выражение, которое называется   определителем (детерминантом) матрицы А, и обозначается так:  
Любой квадратной матрице n-го порядка
| A | = det A= ∆ =
Объяснение нового материала

Способы вычисления определителей
1. Определитель второго порядка задаётся равенством:

2. Определитель третьего порядка задаётся равенством:

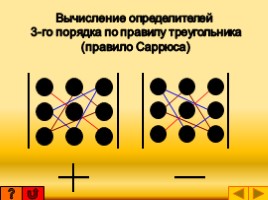
Вычисление определителей 3-го порядка по правилу треугольника (правило Саррюса)

Основные свойства определителей
Если у определителя какая-либо строка (столбец) состоит только из нулей, то определитель равен нулю.

2. Если какие-либо две строки (два столбца) определителя пропорциональны, то определитель равен нулю.
3. Если какую-либо строку (столбец) определителя умножить на любое число, то и весь определитель умножиться на это число.

4. Если две строки (два столбца) определителя поменять местами, то определитель изменит знак.
5. Если к какой-либо строке (столбцу) определителя прибавить, какую-либо другую строку (столбец) умноженную на любое число, то определитель не изменится.

6. Определитель произведения матриц равен произведению определителей.
7. Матрица, определитель которой равен нулю, называется вырожденной; матрица, определитель которой отличен от нуля, называется невырожденной.

Определение:
Минором Mij к элементу aij квадратной матрицы А, называется определитель, составленный из элементов матрицы А, оставшихся после вычёркивания i-строки и j- столбца.
Определение:
Алгебраическим дополнением Aij к элементу aij квадратной матицы А, называется произведение: Aij=(-1)i+j ·Mij

Теорема: (о разложении определителя по элементам строки или столбца).
Сумма произведений элементов любой строки (столбца) определителя на их алгебраические дополнения равна этому определителю, т. е.
Разложение по элементам i-строки:
Разложение по элементам j-столбца:

Задание: Вычислить определитель 4-го порядка.

О П Р Е Д Е Л И Т Е Л Ь
Выберите любую красную букву из данного слова и выполните задание:
Закрепление нового материала

Дайте понятие определителя
Проверь себя!

Равенство определителя 2-го порядка
Проверь себя!

Ты знаешь правило треугольника?
Проверь себя!

Дополнение алгебраическое. Какой формулой задаётся?
Проверь себя!

Aij = (-1)i+j · Mij
МОЛОДЕЦ!!!

Минором Mij к элементу aij квадратной матрицы А, называется определитель, составленный из элементов матрицы А, оставшихся после вычёркивания i-строки и j- столбца.
Определение:

Легко вычисли алгебраическое дополнение А23
Проверь себя!

МОЛОДЕЦ!!!

Домашнее задание

СПАСИБО ЗА ВНИМАНИЕ !

Источники текстовой информации:
 Жевняк Р.М., Карпук А.А. Высшая математика. – Мн.: Выш. шк., 1992.   Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Мн.: Тетрасистемс, 1998. Марков Л.Н., Размыслович Г.П. Высшая математика. Часть 1. –Мн.: Амалфея, 1999. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. I семестр. М.: Новое знание, 2002. Коваленко Н.С., Минченков Ю.В., Овсеец М.И. Высшая математика. Учеб. пособие. -Мн.: ЧИУП, 2003.