Презентация - Планиметрия: вычисление длин и площадей (11 класс)

Задание ЕГЭ ПЛАНИМЕТРИЯ: вычисление длин и площадей
Тренажёр

Надо знать формулы:
Надо уметь:
площади треугольника; площади четырехугольников: прямоугольника, квадрата, ромба, параллелограмма, трапеции; площади круга ; площади сектора.
решать простые планиметрические задачи; производить вычисления по известным формулам.

Площадь можно вычислить:
либо по клеточкам, либо по координатам, либо по формулам.
Количество баллов за правильное решение: 1.

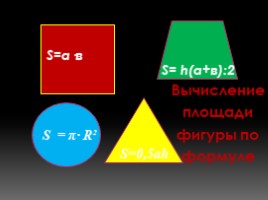
S=а·в
S=0,5ah
S= h(а+в):2
S = π∙ R²
Вычисление площади фигуры по формуле

Задача 1
Ответ: 28
Найдите площадь заштрихованной фигуры, считая стороны квадратных клеток равными 1.
7
4

Задача 2
Найдите площадь ΔABC, считая стороны квадратных клеток равными 1.
Ответ: 9
3
6

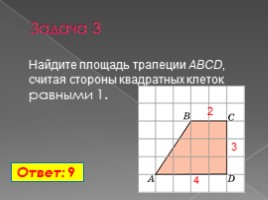
Задача 3
Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
Ответ: 9
2
4
3

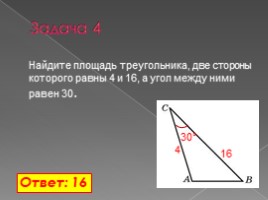
Задача 4
Найдите площадь треугольника, две стороны которого равны 4 и 16, а угол между ними равен 30.
Ответ: 16
30˚
4
16

Задача 5
Боковая сторона равнобедренного треугольника равна 5, а основание равно 8. Найдите площадь этого треугольника.
Ответ: 12
5
5
8
4
4
3

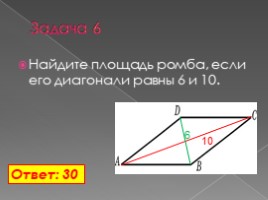
Задача 6
Найдите площадь ромба, если его диагонали равны 6 и 10.
Ответ: 30
6
10

Задача 7
Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите S/π .
Ответ: 1,25
2
1
R
90˚
√5

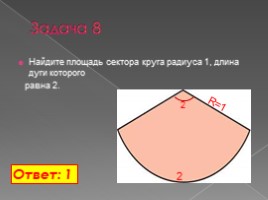
Задача 8
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Ответ: 1
2
R=1
2

Задача 9 (Решите сами)
Ответ: 14
Найдите площадь заштрихованной фигуры, считая стороны квадратных клеток равными 1.

Задача 10 (Решите сами)
Ответ: 15
Найдите площадь заштрихованной фигуры, считая стороны квадратных клеток равными 1.

Задача 11 (решите сами)
Периметр треугольника равен 10, а радиус вписанной окружности равен 2. Найдите площадь этого треугольника.
Ответ: 10

Задача 12 (решите сами)
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 120. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника. В ответе запишите S/√3.
Ответ: 100

Задача 13(решите сами)
Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Ответ: 50

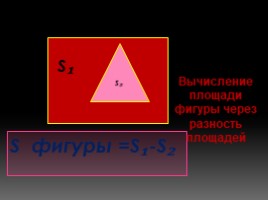
S фигуры =S₁-S₂
S₂
S₁

Вычисление площади фигуры через разность площадей

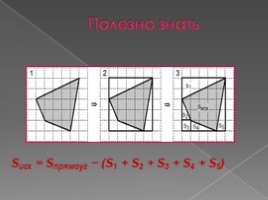
Полезно знать
Sисх = Sпрямоуг − (S1 + S2 + S3 + S4 + S5)

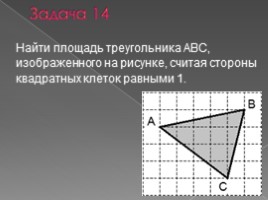
Задача 14
Найти площадь треугольника ABC, изображенного на рисунке, считая стороны квадратных клеток равными 1.

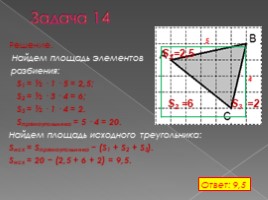
Задача 14
Решение. Найдем площадь элементов  разбиения: S1 = ½ · 1 · 5 = 2,5; S2 = ½ · 3 · 4 = 6; S3 = ½ · 1 · 4 = 2. Sпрямоугольника = 5 · 4 = 20. Найдем площадь исходного треугольника: Sисх = Sпрямоугольника − (S1 + S2 + S3). Sисх = 20 − (2,5 + 6 + 2) = 9,5.
Ответ: 9,5
S₁=2,5
S2 =6
5
4
S3 =2

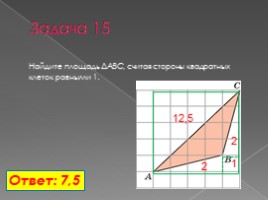
Задача 15
Найдите площадь ΔABC, считая стороны квадратных клеток равными 1.
Ответ: 7,5
12,5
2
1
2

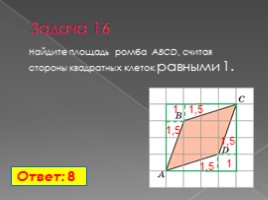
Задача 16
Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1.
Ответ: 8
1
1,5
1,5
1
1,5
1,5

Задача 17
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 2:√π и 4:√π .
Ответ: 12
2:√π
4:√π

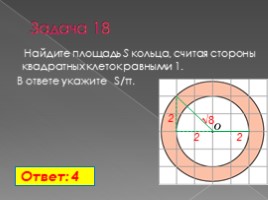
Задача 18
Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите S/π.
Ответ: 4
r=2
R
√8
2
2

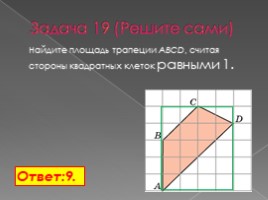
Задача 19 (Решите сами)
Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
Ответ:9.

Задача 20 (Решите сами)
Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Ответ:6

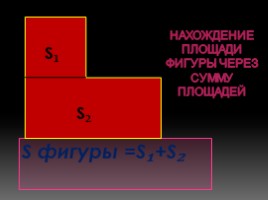
Нахождение площади фигуры через сумму площадей
S фигуры =S₁+S₂
S₁
S₂

Задача 21
Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Ответ: 10
5
5

Задача 22
Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Ответ:8.
2
4

Задача 23
Найдите площадь пятиугольника, считая стороны квадратных клеток равными 1.
Ответ:16.
4
3
2

Задача 24
Найдите площадь фигуры, считая стороны квадратных клеток равными 1.
Ответ:15
1
4
3
1
1

Задача 25
Найдите площадь фигуры, считая стороны квадратных клеток равными 1.
Ответ:13.
4
3
2

1
1
2
2

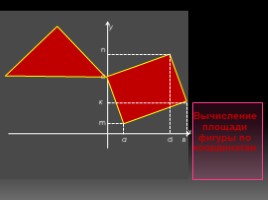
х
у
а
в
с
к
m
n
d
Вычисление площади фигуры по координатам

Задача 26
Найдите площадь треугольника, вершины которого имеют координаты (1; 1), (4; 4), (5;1).
Ответ: 6
4
3

Задача 27
Найдите площадь четырехугольника, вершины которого имеют координаты (1; 0), (0; 2), (4; 4), (5; 2) .
Ответ: 10
5
2

Задача 28
Найдите площадь закрашенной фигуры на координатной плоскости.
Ответ: 24

Сторон Диагоналей Высот Углов
Вычисление элементов фигуры

Задача 29
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 16.
Ответ: 8
16
4
S=64

Задача 30
Найдите диагональ квадрата, если его площадь равна 8.
Ответ: 4
√8
√8
4

Задача 31
Площадь прямоугольного треугольника равна 21. Один из его катетов равен 6. Найдите другой катет.
Ответ:7.
6
S=21

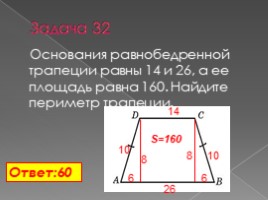
Задача 32
Основания равнобедренной трапеции равны 14 и 26, а ее площадь равна 160. Найдите периметр трапеции.  
Ответ:60
14
26
8
6
6
10
10
S=160
8

Задача 33
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
Ответ: 2

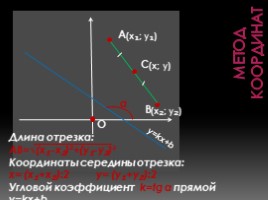
Метод координат
О
А
В
С
(х₁; у₁)
(х₂; у₂)
(х; у)
Длина отрезка: АВ=√(х₁-х₂)²+(у₁-у₂)² Координаты середины отрезка: х= (х₁+х₂):2 у= (у₁+у₂):2 Угловой коэффициент k=tg α прямой у=kx+b.
у=kx+b
α

Задача 29
1.Найдите длину отрезка, соединяющего точки: В(-2;2)и A(6, 8); 2. Найдите расстояние от точки A с координатами (6, 8) до оси абсцисс; 3. Найдите расстояние от точки В до оси ординат. 4. Найдите ординату середины отрезка АВ. 5.Найти ординату точки, симметричной точке А относительно оси ОУ; 6. Найти абсциссу точки, симметричной точке А относительно начала координат.
Ответ:10
Ответ:8
Ответ:2
Ответ:5
Ответ:8
Ответ:-6

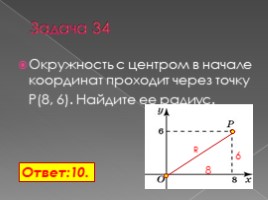
Задача 34
Окружность с центром в начале координат проходит через точку P(8, 6). Найдите ее радиус.
Ответ:10.
R
6
8

Задача 35
Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).
Ответ:5.
R
M

Задача 36
Найдите : 1)угловой коэффициент прямой, проходящей через точки с координатами(2, 0) и (0, 2); 2) угол между прямой и осью ОХ.
Ответ:135.
Ответ:-1.
α
2
2

Задача 37
Точки O(0, 0), A(6, 8), B(6, 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Ответ:6.

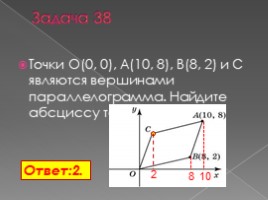
Задача 38
Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C.
Ответ:2.
10
8
2

Координаты вектора АВ(х = х₁ - х₂; у = у₁- у₂)
Длина вектора АВ = √х² + у²= √(х₁-х₂)²+(у₁-у₂)²
Координаты суммы векторов а+b(х₁+х₂ ;у₁+у₂)
Координаты разности векторов а-b(х₁-х₂ ;у₁-у₂)
Координаты вектора умноженного на число:
Векторы
В(х₁; у₁)
А(х₂; у₂)
а(х₁; у₁)
b(х₂; у₂)
kа(kх₁; kу₁)
kа(kх₁; kу₁)

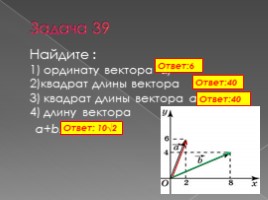
Задача 39
Найдите : 1) ординату вектора а; 2)квадрат длины вектора а; 3) квадрат длины вектора а-b; 4) длину вектора а+b.
Ответ:6
Ответ:40
Ответ:40
Ответ: 10√2

Задача 40
Вектор с началом в точке A(2, 4) имеет координаты (6, 2). Найдите абсциссу точки B.
Ответ:8
8

Задача 41
Две стороны прямоугольника ABCD равны 8 и 6 . Найдите длину суммы векторов АВ и АД.
Ответ:10
8
6

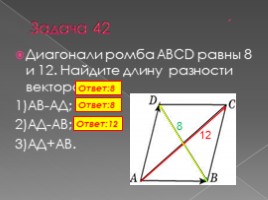
Задача 42
Диагонали ромба ABCD равны 8 и 12. Найдите длину разности векторов: 1)АВ-АД; 2)АД-АВ; 3)АД+АВ. .
Ответ:8
8
12
Ответ:8
Ответ:12

Удачи и успехов!