Презентация - П.31 Конденсаторы. Электроемкость

П.31 Конденсаторы. Электроемкость

Конденсатор
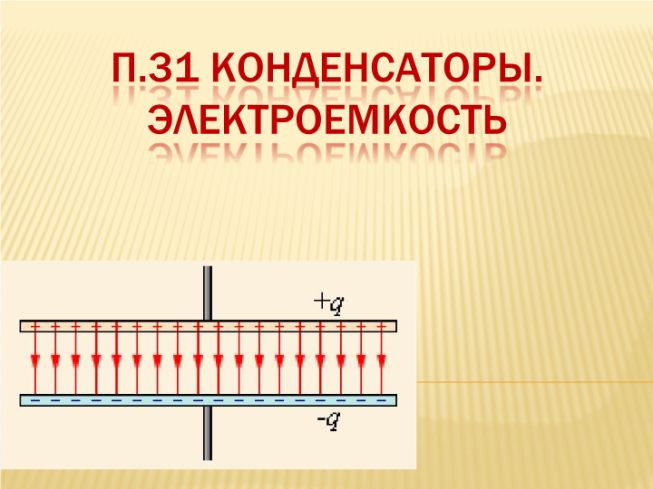
Конденсатор представляет собой два проводника, разделенные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

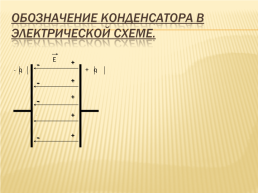
Обозначение конденсатора в электрической схеме.
Е
+
-
- q
+ q
+
-
+
-
+
-
+
-

Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.

Электроемкость конденсатора равна где q – заряд положительной обкладки, U – напряжение между обкладками. Электроемкость конденсатора зависит от его геометрической конструкции и электрической проницаемости заполняющего его диэлектрика и не зависит от заряда обкладок.

Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:
.

Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора, где εo=8,85·10-12Ф/м – электрическая постоянная.
.

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
.

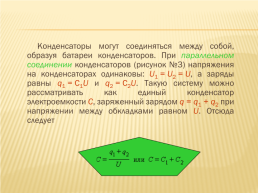
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рисунок №3) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = С2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует
.

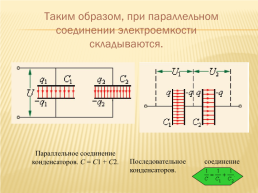
Таким образом, при параллельном соединении электроемкости складываются.
.
Параллельное соединение конденсаторов. C = C1 + C2.
Последовательное соединение конденсаторов.

При последовательном соединении (рисунок 4) одинаковыми оказываются заряды обоих конденсаторов: q1 = q2 = q, а напряжения на них равны и Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2. Следовательно,
.

Типы конденсаторов

Применение конденсаторов
Виды конденсаторов (доклад на выбор):. - воздушный, - бумажный, - слюдяной, - электростатический. Назначение: Накапливать на короткое время заряд или энергию для быстрого изменения потенциала. Не пропускать постоянный ток. В радиотехнике – колебательный контур, выпрямитель. Применение в фототехнике.

Конденсаторы переменной ёмкости с воздушным или твёрдым диэлектриком
Часто используются конденсаторы переменной емкости с воздушным или твёрдым диэлектриком. Они состоят из двух систем металлических пластин, изолированных друг от друга. Одна система пластин неподвижна, вторая может вращаться вокруг оси. Вращая подвижную систему, плавно изменяют ёмкость конденсатора.

задача
Расстояние между пластинами квадратного плоского конденсатора со стороной 20см равно 1мм. Какова разность потенциалов между пластинами, если заряд конденсатора 2 нКл.

Решение:
: