Презентация - Г. Спесер

“Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” ….. писал Г. Спесер, английский философ и социолог.

Тригонометрия - есть измерение треугольников
раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Например, большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Какие основные понятия тригонометрии вам известны?

Тема урока: основные понятия тригонометрии

Древняя Греция
Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

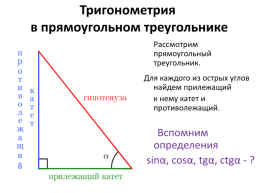
Тригонометрия  в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий. Вспомним определения sinα, cosα, tgα, сtgα - ?

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90°
В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса

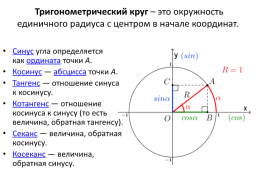
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Синус угла определяется как ордината точки A. Косинус — абсцисса точки A. Тангенс — отношение синуса к косинусу. Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу). Секанс — величина, обратная косинусу. Косеканс — величина, обратная синусу.

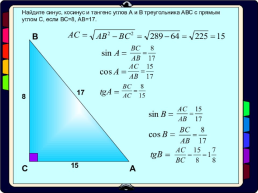
Решаем примеры (1 и 3 вместе, 2 и 4 самостоятельно) стр. 167 № 536 - первая строчка № 537 - первая строчка

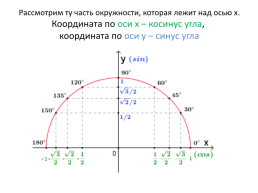
Рассмотрим ту часть окружности, которая лежит над осью x. Координата по оси x – косинус угла,  координата по оси y – синус угла

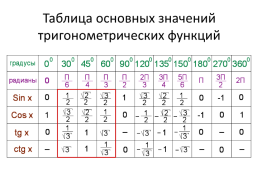
Таблица основных значений тригонометрических функций

Решаем примеры (1 и 3 вместе, 2 и 4 самостоятельно)
Стр. 178 № 562 № 563 Стр. 189 № 600 (1 и 3)

Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sinα, cosα, tgα, ctgα, соотношение sin2α+ cos2α =1

Продолжите фразы:
Сегодня на уроке я узнал… Сегодня на уроке я понял, что мне надо… Сегодня на уроке я повторил… Сегодня на уроке мне было сложно…

Домашнее задание
Электронная библиотека: Стр. 124 № 5 – 8 (чётные) Вспомнить определение, что такое тождество и способы их решения Творческое задание: Подготовить презентацию о знаменитых математических тождествах (Например: Тождество Эйлера)