Слайды и текст этой онлайн презентации
Слайд 1
Как построить график
функции y=f(x+m)+n, если известен график
функции y=f(x)
Слайд 2
Какая из формул задаёт:
- прямую пропорциональность;
-обратную пропорциональность;
-линейную функцию, график которой проходит через начало координат.
2)
1)
Слайд 3
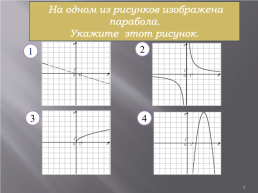
На одном из рисунков изображена парабола. Укажите этот рисунок.
Слайд 4
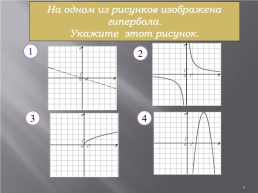
На одном из рисунков изображена гипербола. Укажите этот рисунок.
Слайд 5
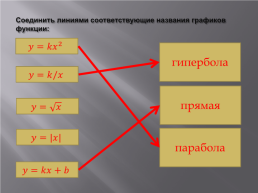
Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола
Слайд 6
Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола
Слайд 7
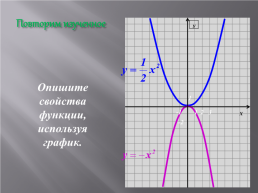
Повторим изученное
У
Опишите свойства
функции, используя
график.
-1
Х
-2
Слайд 8
у
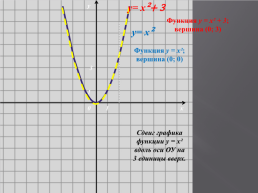
у= х²+ 3
Функция у = х² + 3; вершина (0; 3)
у= х²
Функция у = х²; вершина (0; 0)
х
Сдвиг графика функции у = х² вдоль оси ОУ на
3 единицы вверх.
Слайд 9
у
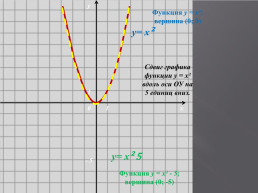
Функция у = х²; вершина (0; 0)
у= х²
Сдвиг графика функции у = х² вдоль оси ОУ на
5 единиц вниз.
х
у= х² 5
- 5
Функция у = х² - 5; вершина (0; -5)
Слайд 10
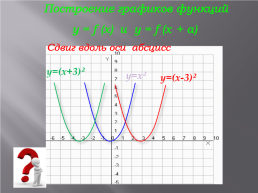
Построение графиков функций
y = f (x) и y = f (x + a)
Сдвиг вдоль оси абсцисс
y=(x+3)²
y=x²
y=(x-3)²
Слайд 11
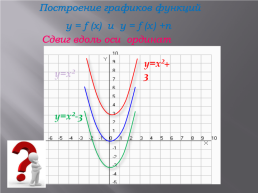
Построение графиков функций
y = f (x) и y = f (x) +n
Сдвиг вдоль оси ординат
y=x²+3
y=x²
y=x²-3
Слайд 12
График функции График функции y = f(x + m) получается параллельным переносом графика функции y=f(x) вдоль оси х на |m| единиц масштаба влево, если m > 0 и вправо, если m< 0
Слайд 13
График функции График функции y = f(x)+n получается параллельным переносом графика функции y=f(x) вдоль оси y на |n| единиц масштаба вверх, если n > 0 и вниз, если n < 0
Слайд 14
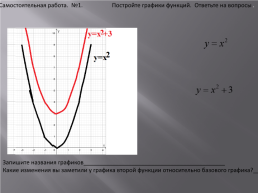
Самостоятельная работа. №1. Постройте графики функций. Ответьте на вопросы.
Запишите названия графиков____________________________________________
Какие изменения вы заметили у графика второй функции относительно базового графика?_________________________
Слайд 15
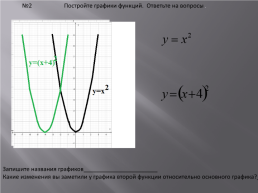
№2 Постройте графики функций. Ответьте на вопросы.
Запишите названия графиков_______________________
Какие изменения вы заметили у графика второй функции относительно основного графика?_____________
Слайд 16
Выводы: основные преобразования графиков элементарных функций:
Сжатие и растяжение графика вдоль
оси y у=k f(x).
Преобразование симметрии относительно оси x у = - f(x)
Сдвиг вдоль оси абсцисс y = f (x + a)
Сдвиг вдоль оси ординат y = f (x) +n
Слайд 17
вправо
вниз
вправо
вверх
Слайд 18
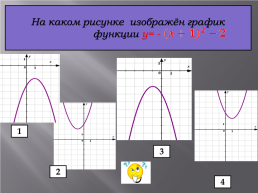
На одном из рисунков изображен график
функции
Укажите номер этого рисунка.
На каком рисунке изображён график
функции y= -
Слайд 19
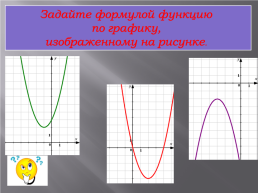
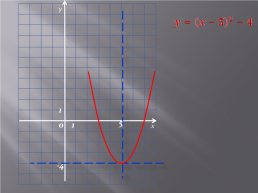
Задайте формулой функцию
по графику,
изображенному на рисунке.
Слайд 21
y
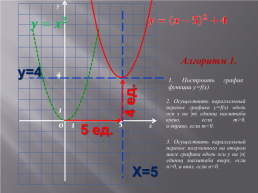
Алгоритм 1.
у=4
1. Построить график функции y=f(x)
4 ед.
2. Осуществить параллельный перенос графика y=f(x) вдоль оси х на |m| единиц масштаба влево, если m>0, и вправо, если m<0.
x
5 ед.
3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |n| единиц масштаба вверх, если n>0, и вниз, если n<0.
Х=5
Слайд 22
y
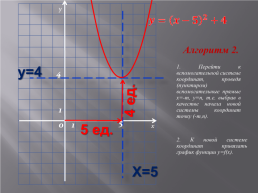
Алгоритм 2.
у=4
1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые х=-m, y=n, т.е. выбрав в качестве начала новой системы координат точку (-m,n).
4 ед.
x
5 ед.
2. К новой системе координат привязать график функции y=f(x).
Х=5
Слайд 26
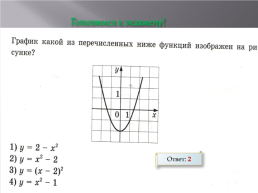
Готовимся к экзамену!
Ответ: 2
Слайд 27
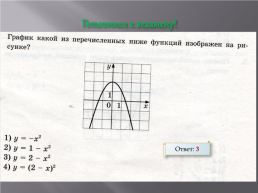
Готовимся к экзамену!
Ответ: 3
 Урок алгебры по теме «Функция y=ax², её график и свойства» с применение системы учебных заданий как средства достижения планируемых результатов ФГОС. 9-й класс
Урок алгебры по теме «Функция y=ax², её график и свойства» с применение системы учебных заданий как средства достижения планируемых результатов ФГОС. 9-й класс Построение и исследование графиков функций с использованием программного обеспечения компьютеров
Построение и исследование графиков функций с использованием программного обеспечения компьютеров Девиз урока. Если путь твой к познанию мира ведет,- как бы ни был он долог и труден- вперед!
Девиз урока. Если путь твой к познанию мира ведет,- как бы ни был он долог и труден- вперед! География 5 класс «Как древние люди представляли себе Вселенную»
География 5 класс «Как древние люди представляли себе Вселенную» Школа как единое образовательное пространство, обеспечивающее формирование функциональной грамотности
Школа как единое образовательное пространство, обеспечивающее формирование функциональной грамотности Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Понятие функции и ее график
Понятие функции и ее график