Презентация - Производная в заданиях ЕГЭ

Производная в заданиях ЕГЭ Открытый урок в 11 классе. Учитель математики МБОУ СОШ№21 Скороходова Н.Ф.

Цель урока: формирование практических навыков решения задач по теме «Производная»
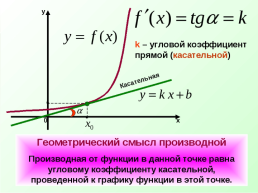
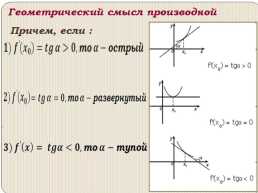
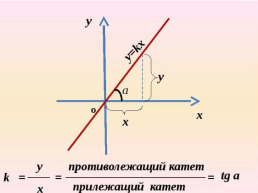
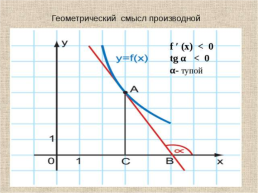
Задачи урока: Повторить теоретические знания по теме «Производная функции и ее геометрический смысл». Научиться решать задачи типа №14 (базовый уровень) из открытого банка заданий для подготовки к ЕГЭ.

«Уча других, мы учимся сами»  Сенека (римский философ)
Хочешь научиться сам – начни учить других!

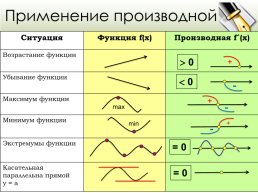
Применение производной
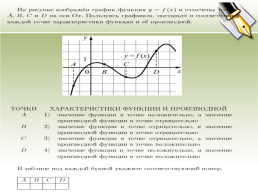
Ситуация.Функция f(x).Производная f´(x)
Возрастание функции..
Убывание функции..
Максимум функции..
Минимум функции..
Экстремумы функции..
Касательная параллельна прямой у = а..
 0
+
 0
-
+
-
max
+
min
-
= 0
= 0

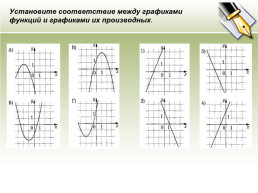
Установите соответствие между графиками функций и графиками их производных.

Ответ: 3421.

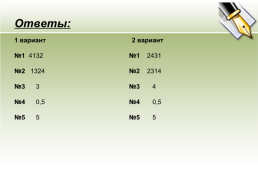
Ответы: 1 вариант 2 вариант №1 4132 №1 2431 №2 1324 №2 2314 №3 3 №3 4 №4 0,5 №4 0,5 №5 5 №5 5

Д/з   Задание №14 из вариантов 1-10

«Итоги»
сегодня я узнал… я понял, что… я попробую… я научился… у меня не получилось … я смогу…

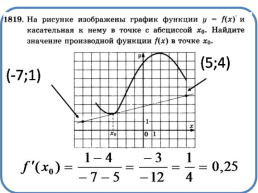
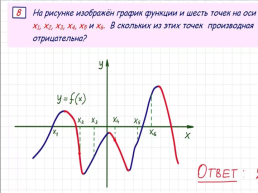
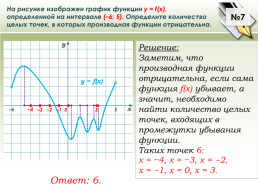
На рисунке изображен график функции у = f(x), определенной на интервале (–6; 5). Определите количество целых точек, в которых производная функции отрицательна.
№7
у
Решение: Заметим, что производная функции отрицательна, если сама функция f(x) убывает, а значит, необходимо найти количество целых точек, входящих в промежутки убывания функции. Таких точек 6: х = −4, х = −3, х = −2, х = −1, х = 0, х = 3.
у = f(x)
х
–6
–4
–1
–2
–3
Ответ: 6.

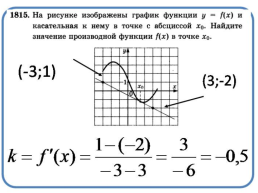
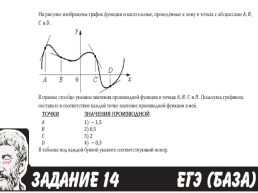
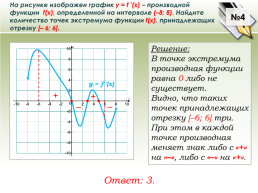
На рисунке изображен график у = f ′(x) – производной функции f(x), определенной на интервале (–8; 8). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [– 6; 6].
№4
Решение: В точке экстремума производная функции равна 0 либо не существует. Видно, что таких точек принадлежащих отрезку [–6; 6] три. При этом в каждой точке производная меняет знак либо с «+» на «–», либо с «–» на «+».
у = f ′(x)
+
+
–
–
Ответ: 3.

«Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника» Ф. Аквинский

Спасибо за урок!