Презентация - “У математиков существует  свой язык – это формулы”. С. Ковалевская

“У математиков существует  свой язык – это формулы”. С. Ковалевская

ПЕРВЫЙ РАУНД

Какой сейчас урок?
Сейчас урок алгебры.

Какой сегодня дежурный звук?
Сегодня дежурные звуки Ч-Ш.

Звуки Ч-Ш нужно говорить правильно, внятно.

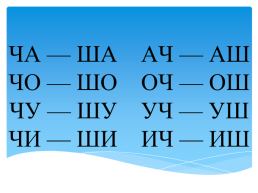
ЧА — ША АЧ — АШ ЧО — ШО ОЧ — ОШ ЧУ — ШУ УЧ — УШ ЧИ — ШИ ИЧ — ИШ

АЧА — АША ОЧО — ОШО ИЧИ — ИШИ УЧУ — УШУ

ШАПКА, ЧАЙНИК, ПОЧТА, КАМЫШ, ЧЕШУЯ, ЧАШКА.

У черепашьего черепашонка на черепашьих лапчонках черепашьи чёботы.

Тема урока:
Формулы сокращенного умножения.

ВТОРОЙ РАУНД

ЗАДАНИЕ:
необходимо записать формулы сокращенного умножения. Первая группа – формула суммы квадрата. Вторая группа – формула разности квадрата. Затем выйдя к доске прочитать.

ТРЕТИЙ РАУНД

ФОРМУЛОЙ называется символьная запись, содержащая некоторое утверждение.

ЗАДАНИЕ:
При записи формул были допущены ошибки. Найдите и исправьте их.

ЗАДАНИЕ:
В таблицах представлены выражения. Выберите правильный ответ.

ЧЕТВЁРТЫЙ РАУНД

1. Что называют многочленом? Ответ: Сумму одночленов. 2. Что называют одночленом? Ответ: Произведение чисел, переменных и их степеней. 3. Какие слагаемые называются подобными? Ответ: Слагаемые с одинаковой буквенной частью.

4. Как привести подобные слагаемые? Ответ: Сложить их числовые коэффициенты, а результат умножить на общую буквенную часть. Ответ: Найти сумму показателей степеней всех входящих в него переменных. 5. Как умножить одночлен на многочлен? Ответ: Одночлен умножить на каждый член многочлена, а результат сложить.

6. Как перемножить одночлены? Ответ: Перемножить числовые коэффициенты, затем перемножить степени с одинаковыми основаниями и результаты перемножить. 7. Как умножить степени с одинаковыми основаниями? Ответ: Основание оставить тем же, а показатели степеней сложить.

8. Как определить степень многочлена? Ответ: Надо определить наибольшую из степеней входящих в него одночленов. 9. Как умножить многочлен на многочлен? Ответ: Каждый член одного многочлена умножить на каждый член другого многочлена и результаты сложить.

ПЯТЫЙ РАУНД

ЗАДАНИЕ:
С помощью формул разложения разности квадратов на множители, найдите значение выражения.

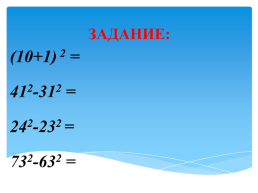
ЗАДАНИЕ:
(10+1) 2 = 412-312 = 242-232 = 732-632 =

ШЕСТОЙ РАУНД

ЗАДАНИЕ:
Задумайте число (до 10). Умножьте его на себя. Прибавьте к результату задуманное число. К полученной сумме прибавьте 1. К полученному числу прибавьте задуманное число.

СЕДЬМОЙ РАУНД

ЗАДАНИЕ:
Найдите ошибку в каждой формуле и исправьте ее на своих листах.
1. (4у-3х)(4у+3х)=8у²-9у²   2. 100х²-4у²=(50х-2у)(50х+2у) 3. (3х+у)²=9х²-6ху+у²           4. (6a-9c)²=36a²-54ac+81c²    5. х³+8=(х+2)(х²-4х+4)

ОТВЕТЫ:
1. (4у-3х)(4у+3х)=8у²-9у² (вместо 8у² должно быть16у²) 2. 100х²-4у²=(50х-2у)(50х+2у) (вместо50х должно быть10х) 3. (3х+у)²=9х²-6ху+у² (вместо-6ху должно быть+6ху) 4. (6a-9c)²=36a²-54ac+81c² (вместо-54ac должно быть-108ac) 5. х³+8=(х+2)(х²-4х+4) (вместо-4х должно быть-2х)

ВОСЬМОЙ РАУНД

ЗАДАНИЕ:
1 ГРУППА 1.Преобразуйте в многочлен: а) (у-4)2 б) (7х+а)2 в) (5с-1)(5с+1) г) (3а+2в)(3а-2в) 2. Упростите выражение. (а-9)2 - (81+2а) 3. Разложите на множители. а) х2-49 б) с2+2ас+а2

ЗАДАНИЕ:
2 ГРУППА 1.Преобразуйте в многочлен: а) (3а+4)2 б) (2х-в)2 в) (с+3)(с-3) г) (5у-2х)(5у+2х) 2. Упростите выражение. (с+в)(с-в) - (5с2-в2) 3. Разложите на множители. а) 25у2-а2 б) 25х2-10ху+у2

ОТВЕТЫ:
1 ГРУППА 1.Преобразуйте в многочлен: а) y2 – 8y + 16 б) 49x2 + 14xa + a2 в) 25 c2 – 1 г) 9a2 – 4b2 2. Упростите выражение. a2 – 18a + 81 – 81 – 2a = a2 – 20a 3. Разложите на множители. а) (x – 7) * (x + 7) б) (c + a)2

ОТВЕТЫ:
2 ГРУППА 1.Преобразуйте в многочлен: а) 9a2 + 24a + 16 б) 4x2 – 4xb + b2 в) c2 – 9 г) 25y2 – 4x2 2. Упростите выражение. c2 – b2 – 5c2 + b2 = c2 – 5c2 3. Разложите на множители. а) (5y – a) * (5y + a) б) (5x – y)2

ДЕВЯТЫЙ РАУНД

За каждый раунд поставьте себе по 5 баллов.

Посчитайте сколько баллов у вас получилось.

ДЕСЯТЫЙ РАУНД