Презентация - Интересные свойства трапеции

Проектная работа « Интересные свойства трапеции » конкурс проектных работ среди обучающихся школ Правобережного района
Выполнила : Тараева Залина ученица 8 класса МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2012 года г.Беслан 2012

Цель работы:
Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства .

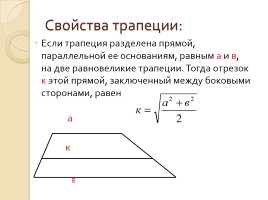
Свойства трапеции:
Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен
a
В
к

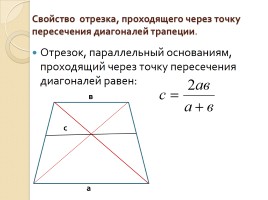
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. 
Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен:
а
в
с

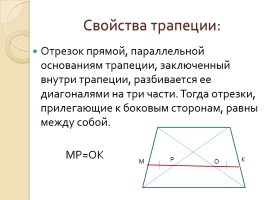
Свойства трапеции:
Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК
Р
М
О
К

Свойства равнобедренной трапеции:
Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
О
О

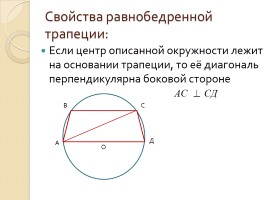
Свойства равнобедренной трапеции:
Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне
О
А
В
С
Д

Свойства равнобедренной трапеции:
В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии.
С
В
А
Д
h

1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства:
1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен

Свойства прямоугольной трапеции, в которую вписана окружность:
1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC

Доказательство :
Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а

I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º .
 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.

I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
 Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

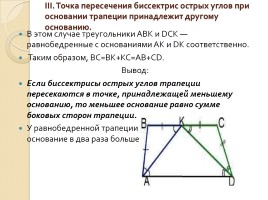
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.  Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.  

IV.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.      

Если равнобедеренную трапецию со сторонами а,в,с,d можно вписать и около неё можно описать окружности, то площадь трапеции равна