Презентация - Да, путь познания не гладок, и знаем мы со школьных лет – загадок больше чем разгадок. И поискам предела нет

Да, путь познания не гладок, и знаем мы со школьных лет – загадок больше чем разгадок. И поискам предела нет.

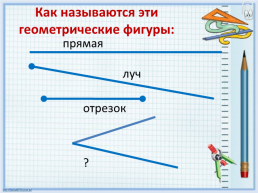
Как называются эти геометрические фигуры:
прямая
луч
отрезок
?

Угол. Прямой и развернутый. Чертежный треугольник. урок математики в 5 классе
Учитель математики Середа Т.В.

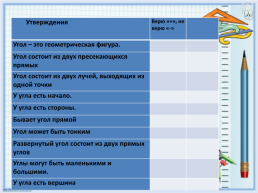
Утверждения.Верю «+», не верю «-».
Угол – это геометрическая фигура...
Угол состоит из двух пресекающихся  прямых..
Угол состоит из двух лучей, выходящих из одной точки..
У угла есть начало...
У угла есть стороны...
Бывает угол прямой..
Угол может быть тонким..
Развернутый угол состоит из двух прямых углов..
Углы могут быть маленькими и большими...
У угла есть вершина..

Задачи урока:
Узнаем: Новую фигуру – угол Какие бывают виды углов

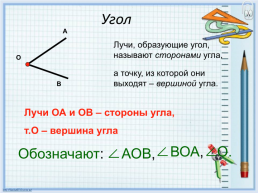
Угол
А
Лучи, образующие угол, называют сторонами угла,
О
а точку, из которой они выходят – вершиной угла.
В
Лучи ОА и ОВ – стороны угла, т.О – вершина угла
ВОА,
О.
Обозначают:
АОВ,

Как построить угол:
Ставим точку и обозначаем её; С началом в данной точке, проводим 2 луча в разные стороны; Обозначаем эти лучи; Записываем название получившегося угла (вершину указываем в середине) используя обозначения угла

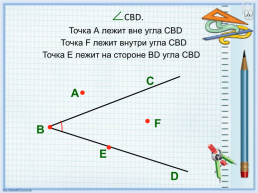
CBD.
Точка A лежит вне угла CBD
Точка F лежит внутри угла CBD
Точка E лежит на стороне BD угла CBD
С
А
F
В
Е
D

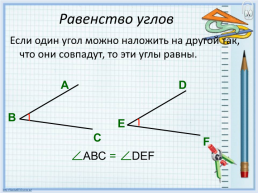
Равенство углов
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
А
D
В
E
С
F
АВС =
DEF

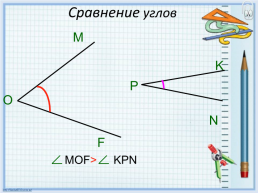
Сравнение углов
M
K
P
O
N
F
MOF>
KPN

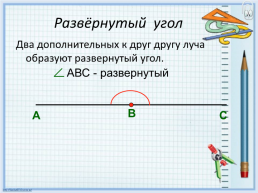
Развёрнутый угол
Два дополнительных к друг другу луча образуют развернутый угол.
АВС - развернутый
В
А
С

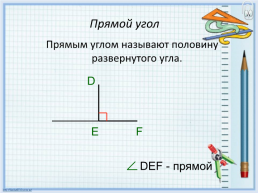
Прямой угол
Прямым углом называют половину развернутого угла.
D
E
F
DEF - прямой

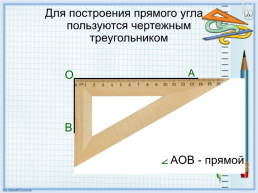
Для построения прямого угла пользуются чертежным треугольником
A
O
B
AOB - прямой

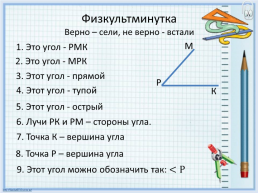
Физкультминутка Верно – сели, не верно - встали
М
1. Это угол - РМК
2. Это угол - МРК
3. Этот угол - прямой
Р
4. Этот угол - тупой
К
5. Этот угол - острый
6. Лучи РК и РМ – стороны угла.
7. Точка К – вершина угла
8. Точка Р – вершина угла
9. Этот угол можно обозначить так:

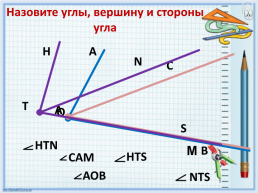
Назовите углы, вершину и стороны угла

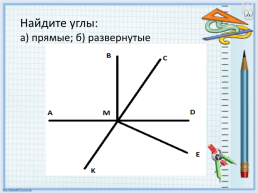
Найдите углы: а) прямые; б) развернутые

№1614

Угол – это геометрическая фигура. Угол состоит из двух лучей, выходящих из одной точки(вершина угла). У угла есть стороны. Бывает угол прямой. Угол бывает развернутый. Прямой угол равен половине развернутого угла.

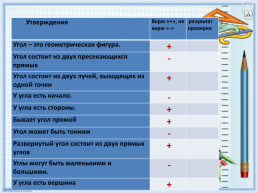
Утверждения.Верю «+», не верю «-».результат проверки
Угол – это геометрическая фигура..+.
Угол состоит из двух пресекающихся  прямых.-.
Угол состоит из двух лучей, выходящих из одной точки.+.
У угла есть начало..-.
У угла есть стороны..+.
Бывает угол прямой.+.
Угол может быть тонким.-.
Развернутый угол состоит из двух прямых углов.+.
Углы могут быть маленькими и большими..-.
У угла есть вершина.+.

Д/з: стр.248 № 1638, 1639, 1640. Записать пословицы и поговорки , где речь идет об угле.

ДО СВИДАНИЯ!
Спасибо за работу на уроке!