Презентация - Векторы

ГОАПОУ «Липецкий металлургический колледж
Векторы
Студент группы ИСиП 20-1 Дехтяренко Владислав

Понятие вектора
Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию его в различных областях математики, механики, а так же в технике.

Что такое вектор?
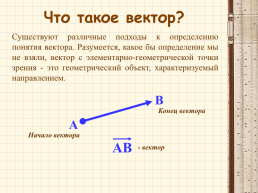
Существуют различные подходы к определению понятия вектора. Разумеется, какое бы определение мы не взяли, вектор с элементарно-геометрической точки зрения - это геометрический объект, характеризуемый направлением.
Конец вектора
Начало вектора
- вектор

Задолго до векторов
Векторы удобны, использование их весьма естественно, и обычно думают, что ими оперируют давно. Но это неверно. Даже в книге Максвелла второй половины 19 века вы не найдете векторных обозначений для производных в декартовой системе координат, с помощью которых обычно записывают полученные им уравнения.
Д. К. Максвелл

Кватернионы
Гораздо раньше векторов в науке были введены кватернионы. Эти величины придумал Гамильтон. Кватернион выражается с помощью четверки чисел. Создатели квантовой механики очень обязаны трудам Гамильтона. Сохранились записи лекций, прочитанных Гиббсом около 1880г в Йельском университете. Хотя векторы и не обозначались в них с помощью жирных букв, но, там дано определение скалярного и векторного произведений и введены символы, соответствующие современным, т.е., в сущности, впервые механика изложена на языке векторов.

Противоречия
Идеи Гиббса об использовании векторов не получили немедленного признания. Например, английский ученый Тейт утверждал, что пользоваться векторами неудобно. Несмотря на оппозицию сторонников кватернионов, после Гиббса векторы стали широко применяться. Языки кватернионов теперь уже не выдвигают на первый план.

Развитие
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.