Презентация - Векторы в пространстве
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 97%
- Слайдов: 79
- Просмотров: 7103
- Скачиваний: 3071
- Размер: 0.79 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Прямоугольная система координат в пространстве. Координаты вектора
Прямоугольная система координат в пространстве. Координаты вектора Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Школа как единое образовательное пространство, обеспечивающее формирование функциональной грамотности
Школа как единое образовательное пространство, обеспечивающее формирование функциональной грамотности Вектор в математике и физике
Вектор в математике и физике Освоение человеком космического пространства
Освоение человеком космического пространства Плоскость. Уравнение плоскости по точке и нормальному вектору
Плоскость. Уравнение плоскости по точке и нормальному вектору Прямые и плоскости в пространстве
Прямые и плоскости в пространстве
Слайды и текст этой онлайн презентации
Слайд 1

Векторы в пространстве
вход
вход
Слайд 2

Содержание
I. Понятие вектора в пространстве II. Коллинеарные векторы III. Компланарные векторы IV. Действия с векторами V. Разложение вектора VI. Базисные задачи Проверь себя Об авторе Помощь в управлении презентацией
Выход
I. Понятие вектора в пространстве II. Коллинеарные векторы III. Компланарные векторы IV. Действия с векторами V. Разложение вектора VI. Базисные задачи Проверь себя Об авторе Помощь в управлении презентацией
Выход
Слайд 3
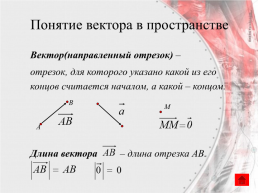
Понятие вектора в пространстве
Вектор(направленный отрезок) – отрезок, для которого указано какой из его концов считается началом, а какой – концом. Длина вектора – длина отрезка AB.
В
M
А
Вектор(направленный отрезок) – отрезок, для которого указано какой из его концов считается началом, а какой – концом. Длина вектора – длина отрезка AB.
В
M
А
Слайд 4

Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Среди коллинеарных различают: Сонаправленные векторы Противоположно направленные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Среди коллинеарных различают: Сонаправленные векторы Противоположно направленные векторы
Слайд 5

Сонаправленные векторы
Сонаправленные векторы - векторы, лежащие по одну сторону от прямой, проходящей через их начала.
Нулевой вектор считается сонаправленным с любым вектором. Равные векторы
Сонаправленные векторы - векторы, лежащие по одну сторону от прямой, проходящей через их начала.
Нулевой вектор считается сонаправленным с любым вектором. Равные векторы
Слайд 6

Равные векторы
Равные векторы - сонаправленные векторы, длины которых равны.
От любой точки можно отложить вектор, равный данному, и притом только один.
Равные векторы - сонаправленные векторы, длины которых равны.
От любой точки можно отложить вектор, равный данному, и притом только один.
Слайд 7

Противоположно направленные векторы
Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала.
Противоположные векторы
Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала.
Противоположные векторы
Слайд 8

Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины которых равны. Вектором, противоположным нулевому, считается нулевой вектор.
Противоположные векторы – противоположно направленные векторы, длины которых равны. Вектором, противоположным нулевому, считается нулевой вектор.
Слайд 9

Признак коллинеарности
Доказательство
Доказательство
Слайд 10

Доказательство признака коллинеарности
Слайд 11

Определение компланарных векторов
Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости. Пример:
B1
C1
A1
D1
B
C
А
D
Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости. Пример:
B1
C1
A1
D1
B
C
А
D
Слайд 12

О компланарных векторах
Любые два вектора всегда компланарны. Три вектора, среди которых имеются два коллинеарных, компланарны.
α
если
Любые два вектора всегда компланарны. Три вектора, среди которых имеются два коллинеарных, компланарны.
α
если
Слайд 13

Признак компланарности
Доказательство Задачи
Доказательство Задачи
Слайд 14

Задачи на компланарность
Компланарны ли векторы: а) б) Справка Решение Известно, что векторы , и компланарны. Компланарны ли векторы: а) б) Справка Решение
Компланарны ли векторы: а) б) Справка Решение Известно, что векторы , и компланарны. Компланарны ли векторы: а) б) Справка Решение
Слайд 15

Решение
Слайд 16

Решение
Слайд 17

Решение
Слайд 18

Доказательство признака компланарности
B1
С
B
A
A1
O
B1
С
B
A
A1
O
Слайд 19

Свойство компланарных векторов
Слайд 20

Действия с векторами
Сложение Вычитание Умножение вектора на число Скалярное произведение
Сложение Вычитание Умножение вектора на число Скалярное произведение
Слайд 21

Сложение векторов
Правило треугольника Правило параллелограмма Правило многоугольника Правило параллелепипеда Свойства сложения
Правило треугольника Правило параллелограмма Правило многоугольника Правило параллелепипеда Свойства сложения
Слайд 22

Правило треугольника
B
А
C
B
А
C
Слайд 23

Правило треугольника
B
А
C
Для любых трех точек А, В и С справедливо равенство:
B
А
C
Для любых трех точек А, В и С справедливо равенство:
Слайд 24

Правило параллелограмма
B
А
C
B
А
C
Слайд 25

Свойства сложения
Слайд 26
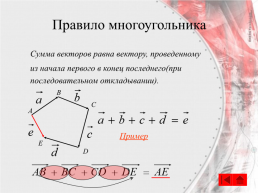
Правило многоугольника
Сумма векторов равна вектору, проведенному из начала первого в конец последнего(при последовательном откладывании).
B
C
A
Пример
E
D
Сумма векторов равна вектору, проведенному из начала первого в конец последнего(при последовательном откладывании).
B
C
A
Пример
E
D
Слайд 27
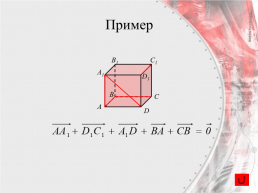
Пример
B1
C1
A1
D1
B
C
A
D
B1
C1
A1
D1
B
C
A
D
Слайд 28

Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
B1
C1
A1
D1
B
C
А
D
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
B1
C1
A1
D1
B
C
А
D
Слайд 29
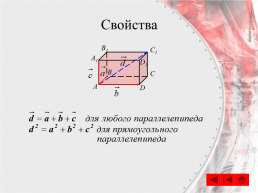
Свойства
B1
C1
A1
D1
B
C
А
D
B1
C1
A1
D1
B
C
А
D
Слайд 30

Вычитание векторов
Вычитание Сложение с противоположным
Вычитание Сложение с противоположным
Слайд 31

Вычитание
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .
Слайд 32

Вычитание
B
A
Правило трех точек
C
B
A
Правило трех точек
C
Слайд 33
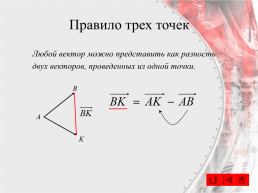
Правило трех точек
Любой вектор можно представить как разность двух векторов, проведенных из одной точки.
B
А
K
Любой вектор можно представить как разность двух векторов, проведенных из одной точки.
B
А
K
Слайд 34

Сложение с противоположным
Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору .
B
А
O
Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору .
B
А
O
Слайд 35

Умножение вектора на число
Слайд 36

Свойства
Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.
Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.
Слайд 37

Свойства
Слайд 38

Скалярное произведение
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Справедливые утверждения Вычисление скалярного произведения в координатах Свойства скалярного произведения
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Справедливые утверждения Вычисление скалярного произведения в координатах Свойства скалярного произведения
Слайд 39

Справедливые утверждения
скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины
скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины
Слайд 40

Вычисление скалярного произведения в координатах
Доказательство
Доказательство
Слайд 41

Доказательство формулы скалярного произведения
B
α
O
A
O
B
A
B
O
A
B
α
O
A
O
B
A
B
O
A
Слайд 42

Доказательство формулы скалярного произведения
Слайд 43

Свойства скалярного произведения
10. 20. 30. 40.
(переместительный закон)
(распределительный закон)
(сочетательный закон)
10. 20. 30. 40.
(переместительный закон)
(распределительный закон)
(сочетательный закон)
Слайд 44

Разложение вектора
По двум неколлинеарным векторам По трем некомпланарным векторам
По двум неколлинеарным векторам По трем некомпланарным векторам
Слайд 45

Разложение вектора по двум неколлинеарным векторам
Теорема. Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство
Теорема. Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство
Слайд 46

Доказательство теоремы
Пусть коллинеарен . Тогда , где y – некоторое число. Следовательно, т.е. разложен по векторам и .
P
B
O
A
A1
Пусть коллинеарен . Тогда , где y – некоторое число. Следовательно, т.е. разложен по векторам и .
P
B
O
A
A1
Слайд 47

Доказательство теоремы
не коллинеарен ни вектору , ни вектору . Отметим О – произвольную точку.
не коллинеарен ни вектору , ни вектору . Отметим О – произвольную точку.
Слайд 48

Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда:
-
Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда:
-
Слайд 49

Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в виде где x, y, z – некоторые числа, то говорят, что вектор разложен по векторам , и . Числа x, y, z называются коэффициентами разложения. Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство
Если вектор p представлен в виде где x, y, z – некоторые числа, то говорят, что вектор разложен по векторам , и . Числа x, y, z называются коэффициентами разложения. Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство
Слайд 50

Доказательство теоремы
P
С
B
P1
P2
O
A
P
С
B
P1
P2
O
A
Слайд 51

Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда:
-
Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда:
-
Слайд 52

Базисные задачи
Вектор, проведенный в середину отрезка
Вектор, проведенный в точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид треугольника
Вектор, проведенный в точку пересечения диагоналей параллелограмма
Вектор, лежащий на диагонали параллелепипеда
Вектор, проведенный в середину отрезка
Вектор, проведенный в точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид треугольника
Вектор, проведенный в точку пересечения диагоналей параллелограмма
Вектор, лежащий на диагонали параллелепипеда
Слайд 53

Вектор, проведенный в середину отрезка,
равен полусумме векторов, проведенных из той же точки в его концы.
Доказательство
равен полусумме векторов, проведенных из той же точки в его концы.
Доказательство
Слайд 54
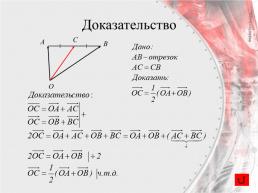
Доказательство
С
A
B
O
С
A
B
O
Слайд 55

Вектор, проведенный в точку отрезка
Точка С делит отрезок АВ в отношении т : п.
С
A
m
n
B
O
Доказательство
Точка С делит отрезок АВ в отношении т : п.
С
A
m
n
B
O
Доказательство
Слайд 56
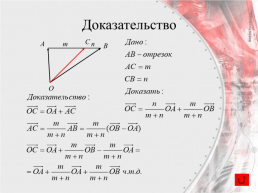
Доказательство
С
A
m
n
B
O
С
A
m
n
B
O
Слайд 57

Вектор, соединяющий середины двух отрезков,
равен полусумме векторов, соединяющих их концы.
N
С
N
D
С
D
B
B
M
M
A
A
Доказательство
равен полусумме векторов, соединяющих их концы.
N
С
N
D
С
D
B
B
M
M
A
A
Доказательство
Слайд 58
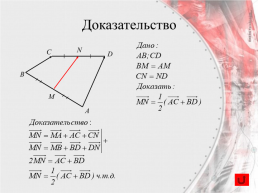
Доказательство
N
С
D
B
M
A
N
С
D
B
M
A
Слайд 59
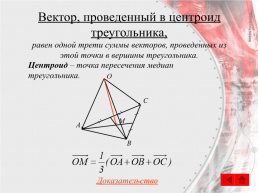
Вектор, проведенный в центроид треугольника,
равен одной трети суммы векторов, проведенных из этой точки в вершины треугольника.
Центроид – точка пересечения медиан треугольника.
O
С
M
A
B
Доказательство
равен одной трети суммы векторов, проведенных из этой точки в вершины треугольника.
Центроид – точка пересечения медиан треугольника.
O
С
M
A
B
Доказательство
Слайд 60
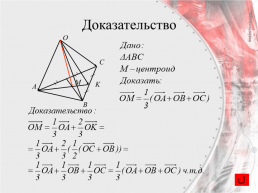
Доказательство
O
С
M
K
A
B
O
С
M
K
A
B
Слайд 61

Вектор, проведенный в точку пересечения диагоналей параллелограмма,
равен одной четверти суммы векторов, проведенных из этой точки в вершины параллелограмма.
O
C
B
M
A
D
Доказательство
равен одной четверти суммы векторов, проведенных из этой точки в вершины параллелограмма.
O
C
B
M
A
D
Доказательство
Слайд 62
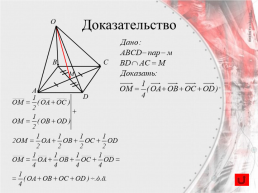
Доказательство
O
B
C
M
A
D
O
B
C
M
A
D
Слайд 63

Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.
B1
C1
A1
D1
B
C
A
D
Доказательство
равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.
B1
C1
A1
D1
B
C
A
D
Доказательство
Слайд 64
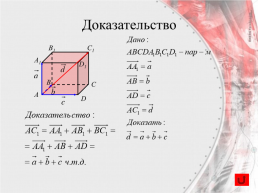
Доказательство
B1
C1
A1
D1
B
C
A
D
B1
C1
A1
D1
B
C
A
D
Слайд 65

Помощь в управлении презентацией
управление презентацией осуществляется с помощью левой клавиши мыши переход от одного слайда к другому и на гиперссылки по одиночному щелчку завершение презентации при нажатии кнопки выход переход к следующему слайду возврат к содержанию возврат к подтеме возврат с гиперссылок
управление презентацией осуществляется с помощью левой клавиши мыши переход от одного слайда к другому и на гиперссылки по одиночному щелчку завершение презентации при нажатии кнопки выход переход к следующему слайду возврат к содержанию возврат к подтеме возврат с гиперссылок
Слайд 66

Проверь себя
Устные вопросы Задача 1. Задача на доказательство Задача 2. Разложение векторов Задача 3. Сложение и вычитание векторов Задача 4. Скалярное произведение
Устные вопросы Задача 1. Задача на доказательство Задача 2. Разложение векторов Задача 3. Сложение и вычитание векторов Задача 4. Скалярное произведение
Слайд 67

Устные вопросы
Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарны? б) любые два коллинеарных вектора сонаправлены? в) любые два равных вектора коллинеарны? г) любые два сонаправленных вектора равны? д) е) существуют векторы , и такие, что и не коллинеарны, и не коллинеарны, а и коллинеарны?
Ответы
Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарны? б) любые два коллинеарных вектора сонаправлены? в) любые два равных вектора коллинеарны? г) любые два сонаправленных вектора равны? д) е) существуют векторы , и такие, что и не коллинеарны, и не коллинеарны, а и коллинеарны?
Ответы
Слайд 68

Ответы
а) ДА б) НЕТ (могут быть и противоположно направленными) в) ДА г) НЕТ (могут иметь разную длину) д) ДА е) ДА
а) ДА б) НЕТ (могут быть и противоположно направленными) в) ДА г) НЕТ (могут иметь разную длину) д) ДА е) ДА
Слайд 69

Задача 1. Задача на доказательство
B1
C1
A1
D1
M2
M1
B
C
А
D
Решение
B1
C1
A1
D1
M2
M1
B
C
А
D
Решение
Слайд 70
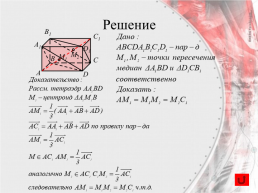
Решение
B1
C1
A1
D1
M2
M1
B
C
А
D
B1
C1
A1
D1
M2
M1
B
C
А
D
Слайд 71
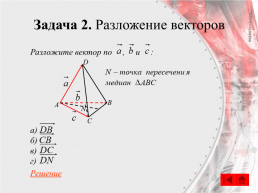
Задача 2. Разложение векторов
Разложите вектор по , и : а) б) в) г) Решение
D
B
A
N
C
Разложите вектор по , и : а) б) в) г) Решение
D
B
A
N
C
Слайд 72

Решение
а) б) в) г)
а) б) в) г)
Слайд 73

Задача 3. Сложение и вычитание
Упростите выражения: а) б) в) г) д) е) Решение
Упростите выражения: а) б) в) г) д) е) Решение
Слайд 74

Решение
а) б) в) г) д) е)
а) б) в) г) д) е)
Слайд 75

Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов:
C1
B1
A1
D1
B
C
A
D
Решение
Вычислить скалярное произведение векторов:
C1
B1
A1
D1
B
C
A
D
Решение
Слайд 76

Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов:
B1
C1
O1
A1
D1
B
C
A
D
Решение
Вычислить скалярное произведение векторов:
B1
C1
O1
A1
D1
B
C
A
D
Решение
Слайд 77

Решение
Слайд 78

Решение
Слайд 79

Решение
B1
C1
O1
A1
D1
B
C
A
D
B1
C1
O1
A1
D1
B
C
A
D
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
