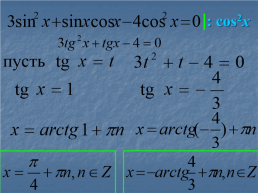Презентация - Решение тригонометрических уравнений

Решение тригонометрических уравнений

Расскажи мне - и я забуду.
Покажи мне - и я запомню.
Дай действовать самому - и я научусь.

Основные формулы тригонометрии

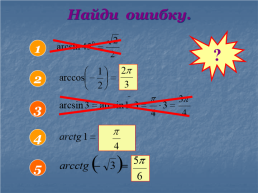
Что называется arcsin a?
Что называется arccos a?

Чему равен arсcos (-a)?
Чему равен arcsin (-a)?

Найди ошибку.
?

Назовите формулу нахождения корней уравнения вида sin x = a?

Назовите формулу нахождения корней уравнения вида cos x = a

Установите соответствие:
sin x = 0
cos x = -1
sin x = 1
cos x = 1
tg x = 1
sin x = - 1
cos x = 0

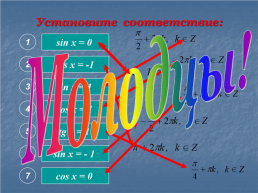
Установите соответствие:
Молодцы!
sin x = 0
cos x = -1
sin x = 1
cos x = 1
tg x = 1
sin x = - 1
cos x = 0

Экспресс-опрос

Слово «тригонометрия» впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое τρίγωνον – треугольник, μετρεω – мера. Иными словами, тригонометрия – наука об измерении треугольников. Тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач в областях астрономии, мореплавания и в составлении географических карт.

Сам термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так называемого «синуса дополнения», т.е. синуса угла, дополняющего данный угол до 90. «Синус дополнения» или ( по латыни) sinus complementi стали сокращенно записывать как sinus co или co-sinus.

Франсуа Виет
Франсуа Виет дополнил и систематизировал различные случаи решения плоских и сферических треугольников, открыл формулы для тригонометрических функций от кратных углов.

Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л. Эйлера.

Однородные тригонометрические уравнения

: cos x

: cos2x

Определите вид уравнения и укажите способ его решения: а) sin x = 2 cos x; б) sin x + cos x = 0; в) 4 cos 3x + 5 sin 3x = 0; г) 1 +7 cos²x + 3 sin²x = 0; д) sin 3x – cos 3x = 0; е) sin x cos x + cos²x = 0