Презентация - Решение неполного уравнения третьей степени

«Решение неполного уравнения третьей степени»    

Теоретическая часть
1. Производная функции ???? / ???? 0 = ???????????? ????→ ???? 0 ???? ???? −???? ???? 0 ????− ???? 0 = ???????????? ∆????→0 ???? ???? 0 +∆???? −???? ???? 0 ∆???? = ???????????? ∆????→0 ∆???? ???? ∆???? . 2. Формула П.Л. Чебышева ???? ????+1 = ???? ???? − ???? ???? ???? ???? / ???? ???? − ???? ???? ???? ???? / ???? ???? 2 ∙ ???? // ???? ???? 2 ???? / ???? ???? , ????=0,1,… 3. Номограммы - графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывания линейки) исследовать функциональные зависимости без вычислений. 4. Алгоритм уточнения корней многочлена, если известны грубо приближенно два значения его корня ???? ???? ≈ ???? ????−2 ???? ???? ????−1 − ???? ????−1 ???? ???? ????−2 ???? ???? ????−1 −???? ???? ????−2

Пример решения уравнения третьей степени Пусть дано уравнение ???? ???? −????????+????=????.
Решение 1. 13-5∙1+1=-3≠0 и −1 3 −5∙ −1 +1=5≠0, значит, целых корней нет.
х ????= ???? 3 −5????+1
-3 −11 3
-2 −11 3
-1 5
0 1 −3
1 1 −3
2 −1 13
3 −1 13
????= ???? 3 −5????+1
???? / =3 ???? 2 −5.
???? / =0;3 ???? 2 −5=0.
????=± 5 3 .
???? ???????????? =− 5 3 ???? ???????????? = 5 3 . , ???? ???????????? ≈− 1+0,6∙ 1 2 , ???? ???????????? ≈1+0,6∙ 1 2 . ???? ???????????? ≈−1,3, ???? ???????????? ≈1,3.
???? ???????????? ≈5, ???? ???????????? ≈−3.
???? 1 ≈−2,2,−3<−2,2<−2; ???? 2 ≈0,2,0<0,2<1; ???? 0 ≈2,1,2<2,1<3. Ответ: −2,2;0,2;2,1.

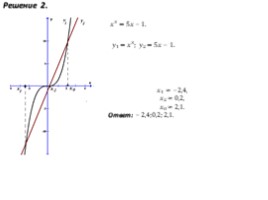
Решение 2.
???? 3 =5????−1.
???? 1 = ???? 3 ; ???? 2 =5????−1.
???? 1 ≈−2,4, ???? 2 ≈0,2, ???? 0 ≈2,1. Ответ: −2,4;0,2;2,1.

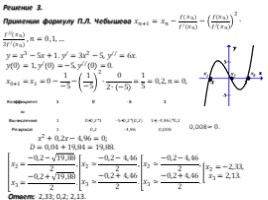
Решение 3. Применим формулу П.Л. Чебышева ???? ????+1 = ???? ???? − ???? ???? ???? ???? / ???? ???? − ???? ???? ???? ???? / ???? ???? 2 ∙ ???? // ???? ???? 2 ???? / ???? ???? , ????=0,1,…

????= ???? 3 −5????+1. ???? / =3 ???? 2 −5, ???? // =6????. ???? 0 =1, ???? / 0 =−5, ???? // 0 =0. ???? 0+1 = ???? 1 =0− 1 −5 − 1 −5 2 ∙ 0 2∙ −5 = 1 5 =0,2, ????=0,
Коэффициенты 1 0 -5 1
Вычисления 1 0+0,2*1 -5+0,2*(0,2) 1+(-4,96)*0,2
Результат 1 0,2 -4,96 0,008
0,008≈0.
???? 2 +0,2????−4,96=0; ????=0,04+19,84=19,88. ???? 2 = −0,2− 19,88 2 , ???? 3 = −0,2+ 19,88 2 . ???? 2 ≈ −0,2−4,46 2 , ???? 3 ≈ −0,2+4,46 2 . ???? 2 ≈ −0,2−4,46 2 , ???? 3 ≈ −0,2+4,46 2 . ???? 2 =−2,33, ???? 3 =2,13. Ответ: -2,33; 0,2; 2,13.

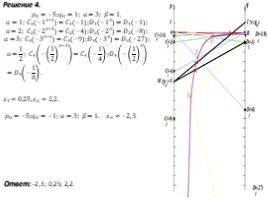
Решение 4.
???? 0 =−5; ???? 0 =1; ????=3; ????=1. ????=1; ???? 1 − 1 3−1 = ???? 1 −1 ; ???? 1 − 1 3 = ???? 1 −1 ; ????=2; ???? 2 − 2 3−1 = ???? 2 −4 ; ???? 2 − 2 3 = ???? 2 −8 ; ????=3; ???? 3 − 3 3−1 = ???? 3 −9 ; ???? 3 −3 3 = ???? 3 −27 ; ????= 1 2 ; ???? 4 − 1 2 3−1 = ???? 4 − 1 4 ; ???? 4 − 1 2 3 = ???? 4 − 1 8 .
???? 1 ≈0,25, ???? 2 ≈2,2.
???? 0 =−5; ???? 0 =−1; ????=3; ????=1.
???? 3 ≈−2,3.
Ответ: -2,3; 0,25; 2,2.

Проверим полученные корни с помощью Интернет ресурсов: сайта Решение уравнений бесплатно - Калькулятор Онлайн Обычные уравнения
Ответ: 0,2; 2,13; -2,33.

Уточним один из корней многочлена, полученные в Решении 4 с помощью алгоритма уточнения корней многочлена
Возьмём ???? 1 ≈0,25, ????=1. ???? 1 ≈0,25, ???? 0,25 = 0,25 3 −5∙0,25+1=−0,234375, ????=1, ???? 1 =−5. ???? 3 = 0,25∙ −5 −1∙ −0,234375 −5+0,234375 = −1,25+0,234375 −4,765625 = 1,015625 4,765625 ≈0,21 ???? 0,21 =0,009261−5∙0,21+1=−0,040739. ???? 4 = 0,25∙ −0,04 −0,21∙ −0,234375 −0,04+0,234375 = 0,03921875 0,194375 ≈0,0202. Можно продолжить уточнение приближенного значения корня. Примем за приближенного значения корня число 0,0202.

Вывод
Способ решения Недостатки Преимущества
Построение графика функции и определение приближенного значения нулей функции с помощью таблицы зависимости х от у. Времяемкий, встречается проблема оценивания значения иррационального числа. Погрешность в нахождении одного из трех корней. Наглядный.Интересно оценивание корней с помощью свойства непрерывных функций (знакопостоянство и нули функции). Может быть применен к большинству алгебраических уравнений.
Графический способ решения уравнения Неточный. Погрешность в нахождении одного из трех корней. Наглядный, дает право выбора введения вспомогательных функций.
Применение формулы П.Л. Чебышева Громоздкие вычисления, чтобы их избежать прибегли к теории многочленов для нахождения двух корней. Корни найдены достаточно точно.
Применение номограммы Времяемкий, требует точности в построении графика функции, в масштабе, аккуратности. Корни найдены достаточно точно.