Презентация - Решение простейших тригонометрических уравнений

“Уравнение -  это золотой ключ, открывающий все математические сезамы”. Станислав Коваль
ГАПОУ «ЧТТПиК»

Решение простейших тригонометрических уравнений
ГАПОУ «ЧТТПиК»

Цель:
закрепление умения решать простейшие тригонометрические уравнения вида sin t = a, cos t = a, tg t = a, ctg t = a в ходе решения примеров

Повторение
Когда тригонометрическое уравнение вида sin t = a, cos t = a, tg t = a, ctg t = a не имеет решений?

Что необходимо знать, чтобы решить любое тригонометрическое уравнение?

Общие формулы решения простейших тригонометрических уравнений

Общие формулы решения простейших тригонометрических уравнений cos t = a, sin t = a.

Общие формулы решения простейших тригонометрических уравнений.
sin t = а, |a|≤1 t = 2. cos t = a, |a|≤1 t =
Если то решений нет

Общие формулы решения простейших тригонометрических уравнений tg t = a, ctg t = a.

Общие формулы решения простейших тригонометрических уравнений.
tg t = а, t = 2. ctg t = a, t =

Дайте определение арксинуса, арккосинуса, арктангенса и арккотангенса
Арксинусом числа a называется такое число из отрезка [-π/2 ; π/2], синус которого равен a. Арккосинусом числа a называется такое число из отрезка [0; π], косинус которого равен a. Арктангенсом числа a называется такое число из интервала (-π/2 ; π/2), тангенс которого равен a. Арккотангенсом числа a называется такое число из интервала (0; π), котангенс которого равен a.

Как находят арксинусы, арккосинусы, арктангенсы и арккотангенсы отрицательных чисел?
arcsin (-a) = - arcsin a arccos (-a) = - arccos a arctg (-a) = - arctg a arcctg (-a) = - arcctg a

Существуют ли такие случаи, когда решение уравнения находят не по общей формуле?

Проверка домашнего задания: Заполните таблицу частных решений
a=1 a=0 a = -1

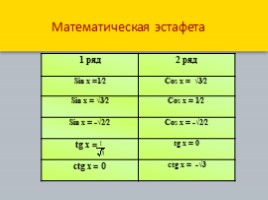
Математическая эстафета
1 ряд 2 ряд
Sin x =1∕2 Cos x = √3∕2
Sin x = √3∕2 Cos x = 1∕2
Sin x = -√2∕2 Cos x = -√2∕2
tg x = tg x = 0
сtg x = 0 сtg x = -√3

Математическая эстафета Проверка
1 ряд 2 ряд
х = (-1) π ∕6 + πк, к Є Z х = π∕6+ 2 π n; n Є Z
х = (-1) π∕3+πк, к Є Z х = π∕3+ 2 π n; n Є Z
х = (-1) π∕4+πn, n Є Z х = 3π∕4+ 2 π n; n Є Z
х = π∕6 + πn, n Є Z х = π n; n Є Z
х не существует х = 5π∕6+ π n; n Є Z

«Алгебра и начало анализа 10-11 класс. / под ред. А.Н.Колмогоров. – М.: Просвещение, 2010 г. стр.75 № 146 в), г).
Решение задач по учебнику

Выполнение самостоятельной работы в форме теста

Эталон ответов: 1 вариант А 2. В 3.В 2 вариант Б 2. А 3.А Критерии выставления оценок 3 верных ответа- «отлично», 2 - «хорошо», 1 – «удовлетворительно».

ДОМАШНЕЕ ЗАДАНИЕ: № 146 а) б) № 147 в) Дополнительное задание решить уравнение