Презентация - Динамика свободных колебаний

Динамика свободных колебаний

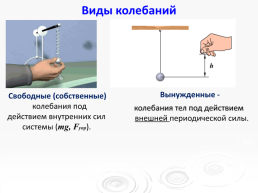
Виды колебаний
Вынужденные - колебания тел под действием внешней периодической силы.
Свободные (собственные) колебания под действием внутренних сил системы (mg, Fупр).

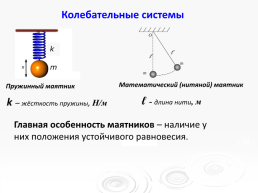
Колебательные системы
k
m
Математический (нитяной) маятник
Пружинный маятник
ℓ - длина нити, м
k – жёсткость пружины, Н/м
Главная особенность маятников – наличие у них положения устойчивого равновесия.

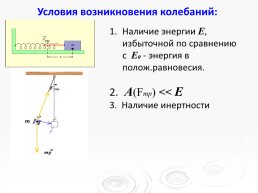
Условия возникновения колебаний:
Наличие энергии Е, избыточной по сравнению с Е₀ - энергия в полож.равновесия. А(Fтр) << Е 3. Наличие инертности

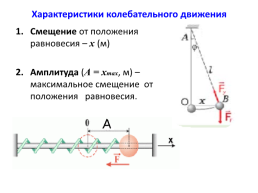
Характеристики колебательного движения
Смещение от положения равновесия – х (м) Амплитуда (А = хmax, м) – максимальное смещение от положения равновесия.

3. Период T (с) – время одного полного колебания. 4. Частота ν (Гц = 1/с = с¯¹) – число колебаний в единицу времени. 5. Циклическая частота ω (рад/с = с¯¹ ) - число колебаний за 2π секунд.

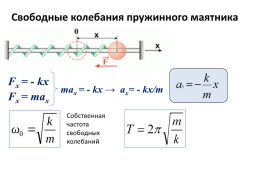
Свободные колебания пружинного маятника
Fx = - kx Fx = max
max = - kx → ax= - kx/m
Собственная частота свободных колебаний

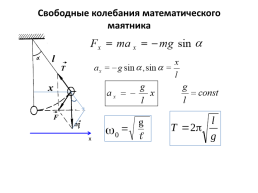
Свободные колебания математического маятника
l
T
x
F
х

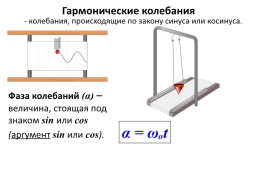
Гармонические колебания
- колебания, происходящие по закону синуса или косинуса.
Фаза колебаний (α) – величина, стоящая под знаком sin или cos (аргумент sin или cos).
α = ωₒt

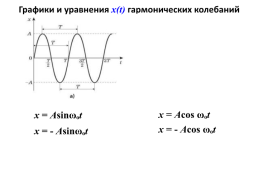
Графики и уравнения х(t) гармонических колебаний
x = Аcos ωₒt
x = Аsinωₒt
x = - Аcos ωₒt
x = - Аsinωₒt

х
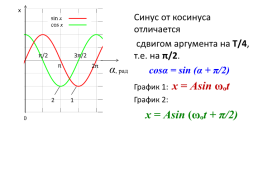
Синус от косинуса отличается сдвигом аргумента на Т/4, т.е. на π/2. cosα = sin (α + π/2) График 1: x = Аsin ωₒt График 2: x = Аsin (ωₒt + π/2)
π/2
3π/2
π
α, рад
2π

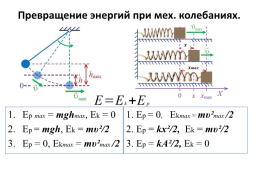
Превращение энергий при мех. колебаниях.
х
хmax
Ер max = mghmax, Еk = 0 Ер = mgh, Еk = mυ²/2 Ер = 0, Еkmax = mυ²max /2
1. Ер = 0, Еkmax = mυ²max /2 2. Ер = kx²/2, Еk = mυ²/2 3. Ер = kА²/2, Еk = 0

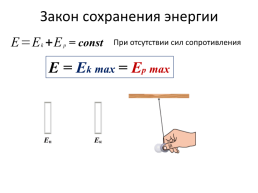
Закон сохранения энергии
= const
При отсутствии сил сопротивления
Е = Еk max = Еp max

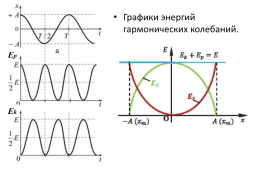
Графики энергий гармонических колебаний.
Ер
Еk