Презентация - Тригонометрия в окружающем нас мире и в жизни человека..

Тригонометрия в окружающем нас мире и в жизни человека.
Работу выполнила Студентка группы 1Б Ганагина Светлана Владимировна

Введение
Тригонометрия-это раздел математики, изучающий тригонометрические функции. Сложно представить, но с этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Вы могли не подозревать об этом, но тригонометрия встречается в таких науках, как физика, биология, не последнюю роль она играет и в медицине, и, что самое интересное, без неё не обошлось даже в музыке и архитектуре.

История
Тригонометрия-(от греч. Trigwnon-треугольник и metrew-измеряю). По звёздам вычисляли местонахождения корабля в море. Древние люди вычисляли высоту дерева, сравнивая длину его тени с длиной тени от шеста, высота которого была известна.

Арабские Зиджи
Улугбек (1394-1449)- основатель научной школы в Самарканде. Первые трактаты о плоской тригонометрии (X-XI вв.).

Древняя Греция
Потребность в решении треугольников раньше всего возникла в астрономии: и в течении долгого времени тригонометрия развивалась и изучалась как один из отделов астрономии. Насколько известно: способы решения треугольников (сферических) первые были письменно изложены греческим астрономом Гиппархом в середине 2 века до н.э. Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею( 2 век н.э.), создателю геоцентрической системы мира, господствовавшей до Коперника. Греческие астрономы не знали синусов, косинусов и тангенсов.

Древняя Греция
Вместо таблиц этих величин они употребляли таблицы: позволяющие отыскать хорду окружности по стягиваемой дуге. Дуги измерялись в градусах и минутах; хорды тоже измерялись градусами (один градус составлял шестидесятую часть радиуса), минутами и секундами. Это шестидесятеричное подразделение греки заимствовали у вавилонян.

Индия
Значительные высоты достигла тригонометрия и у индийских средневековых астрономов. Главным достижением индийских астрономов стала: Замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом в Индии было положено начало тригонометрии как учению о тригонометрических величин. Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые используются в современной науке.

Индия
Индийцы также знали: Формулы для кратких углов sin na, cos nа, где n=2,3,4,5. Первая таблица синусов «Сурья-сиддханте» у Ариабхаты. Она приведена через 3,45. Позднее ученые составили более подробные таблицы: например Бхаскара приводит таблицу синусов через 1. Южноиндийские математики в 16 веке добились больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа П.Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 веках.

Европа
Ряды для синуса и косинуса вывел И.Ньютон в 1666 г., Ряд арктангенса найден Дж.Грегори в 1671 г. и Г.В.Лейбницем в 1673 г. Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476)). Региомонтан составил также подробные тригонометрические таблицы; Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543)- творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трём данным.

Россия
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году. И.Бернулли в письме к петербургскому математику Л.Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращённые обозначения тригонометрических функций угла х:tang x, cos x, sin x, cotg x. Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга.

Значимые люди в тригонометрии
~Таблица числовых значений хорд. ~Таблица для определения соотношений между элемента треугольников. ~Первая таблица синусов, вычитанная по хордам в окружности. ~«Альмагест»- самая значимая тригонометрическая работа всей античности.

~Построил таблицы тангенсов, котангенсов и косекансов.
~Присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. ~Установил основные соотношения между этими линиями. ~Установил формулу двойного угла.

~Автор трактата о полном четырёхстороннике. ~Построил таблицы синусов и котангенсов.

~Дополнил и систематизировал различные случаи решения плоских и сферических треугольников. ~Открыл «плоскую» теорему косинусов и формулы тригонометрических функций от кратных углов. ~Разложил функции в ряды и открыл путь для их использования в математическом анализе.

~Ввёл понятие функции и принятую в наши дни символику. ~Разъяснил вопрос о знаках всех тригонометрических функций любого аргумента. ~Разработал метод проектирования сложных форм в 1920 году. ~Выразил тригонометрические функции как отношение координат х, у,z к длине элемента.

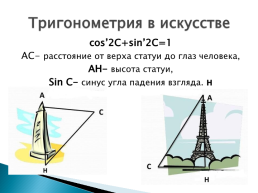
Тригонометрия в искусстве
cos’2C+sin’2C=1 АС- расстояние от верха статуи до глаз человека, АН- высота статуи, Sin C- cинус угла падения взгляда. н
Н

Тригонометрия в физике
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями. Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания:

Тригонометрия и тригонометрические функции в медицине и биологии.
Одно из фундаментальных свойств живой природы- это цикличность большинства происходящих в ней процессов. Биологические ритмы, биоритмы- это более или менее регулярные изменения характера и интенсивности биологических процессов. Основной земной ритм- суточный. Модель биоритмов можно построить с помощью тригонометрических функций.

Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчёта(день ,месяц ,год) и длительность прогноза (кол-во дней).

Американские учёные утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус. Тригонометрия играет важную роль в медицине. С её помощью иранские учёные открыли формулу сердца- комплексное алгебраически- тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчётов в случаях аритмии.

Тригонометрия в архитектуре.
Детская школа Гауди в Барселоне.

Сантьяго Калатрава Винодельня «БодегасИсиос».

Тригонометрия в музыке.
Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики. Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…. Диатоническая гамма 2:3:5

Тетраэдр из различных типов аккордов четырёх звуков: Синий- малые интервалы; Более тёплые тона; Более «разряженные» звуки аккорда; Красная сфера- наиболее гармоничный аккорд с равными интервалами между нотами.