Презентация - Круг окружность элементы

1
Решение задач

1
Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.
Рисунок
Решение(11)
- по условию
А
прямоугольный
= 3
В
О
D
с² = а² + b² Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов.
равнобедренный
С
Ответ

2
В треугольнике ABC угол C равен 90°, AC = 30 , BC = √13. Найдите радиус окружности, описанной около этого треугольника.
Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы.
Рисунок
Решение(8)
В
По теореме Пифагора
О
= 35
С
А
17,5
Ответ

3
Найдите величину (в градусах) вписанного угла α, опирающегося на хорду  AB, равную радиусу окружности.
Центральный угол равен градусной мере дуги на которую он опирается Вписанный угол равен половине дуги на которую он опирается
Рисунок(2)
Решение(6)
С
О
равносторонний
А
В
Ответ

4
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Рисунок(2)
Решение(5)
О
прямоугольный
По теореме Пифагора:
А
В
Ответ

5
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Угол, образованный касательной и хордой измеряется половиной дуги, заключенной между его сторонами
Рисунок
Решение(6)
М
О
равнобедренный
К
Ответ

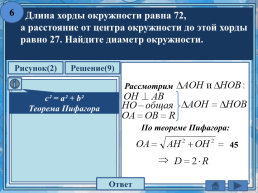
6
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Рисунок(2)
Решение(9)
Рассмотрим
с² = а² + b² Теорема Пифагора
О
По теореме Пифагора:
Н
А
В
С
Ответ

7
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Радиус окружности перпендикулярен касательной в точке касания
Рисунок(2)
Решение(5)
В
А
D
прямоугольный
По теореме Пифагора:
О
Ответ

8
На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окр-ти.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Рисунок(2)
Решение(5)
А
В
C
прямоугольный
По теореме Пифагора:
H
Ответ

9
Окружность радиусом 39 вписана в квадрат. Найдите площадь квадрата.
Сторона квадрата равна диаметру вписанной в него окружности
Рисунок
Решение(3)
R
О
Ответ

10
Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен половине высоты трапеции.
Рисунок
Решение(2)
R
О
Ответ

11
Радиус вписанной в квадрат окружности равен 2√2 Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности вдвое меньше её стороны.
Рисунок
Решение(4)
R
a
О
Ответ

12
Радиус окружности, описанной около квадрата, равен 4√ 2 . Найдите радиус окружности, вписанной в этот квадрат.
Радиус описанной вокруг квадрата окружности равен половине его диагонали.
Рисунок
Решение(6)
D
C
R
r
Сторона квадрата вдвое больше радиуса вписанной в него окружности.
О
B
A
Ответ

13
Хорды AC и BD окружности пересекаются в точке P, BP = 15, CP = 6, DP = 10. Найдите AP.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды
Рисунок
Решение(3)
В
С
P
D
О
А
Ответ

14
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Центральный угол равен градусной мере дуги на которую он опирается
Рисунок(2)
Решение(6)
центральный
равнобедренный
О
А
С
В
Ответ

15
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окр-ти в точке K. Другая прямая пересекает окр-ть в точках B и C, причём AB = 2, AC = 8. Найдите AK.
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть
Рисунок
Решение(3)
С
О
В
А
К
Ответ

16
Радиус окружности, вписанной в равносторонний треугольника равна 3 . Найдите длину стороны этого треугольника.
2√
Рисунок
Решение(5)
равносторонний
С
a
О
r
В
А
Ответ

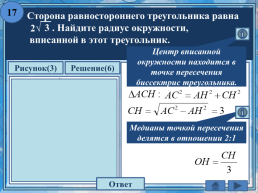
17
Сторона равностороннего треугольника равна 3 . Найдите радиус окружности, вписанной в этот треугольник.
2√
Центр вписанной окружности находится в точке пересечения биссектрис треугольника.
Рисунок(3)
Решение(6)
С
Медианы точкой пересечения делятся в отношении 2:1
О
Н
В
А
Ответ

Фон слайдов
Учительница
Банк заданий ФИПИ