Презентация - Объем призмы

Объем призмы

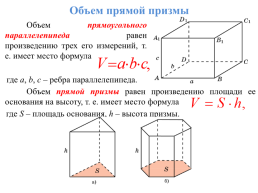
Объем прямой призмы
Объем прямоугольного параллелепипеда равен произведению трех его измерений, т. е. имеет место формула
где a, b, c – ребра параллелепипеда.
Объем прямой призмы равен произведению площади ее основания на высоту, т. е. имеет место формула
где S – площадь основания, h – высота призмы.

Задача 1
Как относятся объемы двух кубов: данного и его модели, уменьшенной в масштабе: а) 1 : 2; б) 1 : 3; в) 1 : n?
а) Коэффициент подобия полученных кубов будет составлять . Объемы подобных тел соотносятся как , поэтому отношение объемов будет 1:8. б) Аналогично . Соотношение равно 1:27. в) Обобщаем для любого числа n: . Отношение 1: n3.
Ответ: а) 1 : 8;
б) 1 : 27;
в) 1 : n3.

Задача 2
Площадь поверхности куба равна 24. Найдите его объем.
, находим сторону куба: Тогда объем: куб. ед.
Ответ: 8.

Задача 3
Как изменится объем прямого параллелепипеда, если: а) одно из его измерений увеличить в 2 раза, в 3 раза, в n раз; б) если два его измерения увеличить, причем каждое из них в 2, 3, n раз; в) если все три его измерения увеличить в 2, 3, n раз?
а) Пусть увеличили измерение а, тогда , , . б) Пусть увеличили измерения а и b, тогда , , . в) Пусть увеличили все измерения, тогда , , .
Ответ: а) Увеличится в 2 раза, в 3 раза, в n раз;
б) увеличится в 4 раза, в 9 раза, в n2 раз;
в) увеличится в 8 раз, в 27 раз, в n3 раз.

Задача 4
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3. Каким должно быть третье ребро, выходящее из той же вершины, чтобы объем этого параллелепипеда равнялся 30?
Ответ: 5.

Задача 5
Основанием аквариума является прямоугольник со сторонами 40 см и 50 см. Уровень воды в нем находится на высоте 80 см. Эту воду перелили в другой аквариум, основанием которого является прямоугольник со сторонами 80 см и 100 см. На какой высоте будет находиться уровень воды?
Обозначим объем первоначального аквариума , а второго . Найдем : см3. Тогда см3, откуда см.
Ответ: 20 см.

Задача 6
Сколько коробок в форме прямоугольного параллелепипеда размерами (см) можно поместить в кузов машины размерами (м)?
Пусть объем коробки, а объем кузова машины. Переводим размеры коробки в м: см м Найдем : м3. Объем кузова: м3. Отношение объемов . Значит в кузове машины можно разместить 150 таких коробок.
Ответ: 150.

Задача 7
Чему равен объем пространственного креста, если ребра образующих его кубов равны единице?
Можем заметить, что пространственный крест состоит из 7 кубов, значит его объем будет равен их суммарному объему: куб. ед., тогда куб. ед.
Ответ: 7.

Задача 8
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Данный Многогранник составлен из двух прямоугольных параллелепипедов, найдем их объемы:
куб. ед., куб. ед.,
Тогда их суммарный объем: куб. ед.
Ответ. 12.

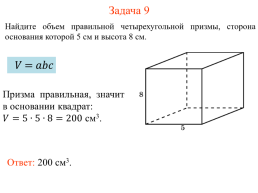
Задача 9
Найдите объем правильной четырехугольной призмы, сторона основания которой 5 см и высота 8 см.
Призма правильная, значит в основании квадрат: см3.
Ответ: 200 см3.

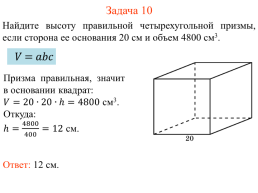
Задача 10
Найдите высоту правильной четырехугольной призмы, если сторона ее основания 20 см и объем 4800 см3.
Призма правильная, значит в основании квадрат: см3. Откуда: см.
Ответ: 12 см.

Задача 11
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем данной призмы.
В основании прямоугольный треугольник, его площадь равна половине произведения катетов: см2. Высота по условию равна 10 см: см3.
Ответ: 60 см3.

Задача 12
Найдите объем правильной 6-угольной призмы, высота которой равна 12, а сторона основания равна 5.
В основании правильный шестиугольник, его площадь равна: см2. Высота по условию равна 12 см: см3.
Ответ: см3.

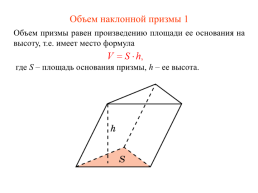
Объем наклонной призмы 1
Объем призмы равен произведению площади ее основания на высоту, т.е. имеет место формула
где S – площадь основания призмы, h – ее высота.

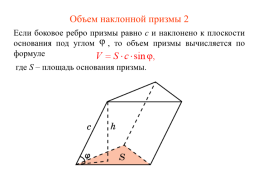
Объем наклонной призмы 2
Если боковое ребро призмы равно c и наклонено к плоскости основания под углом , то объем призмы вычисляется по формуле
где S – площадь основания призмы.

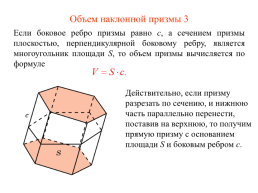
Объем наклонной призмы 3
Если боковое ребро призмы равно c, а сечением призмы плоскостью, перпендикулярной боковому ребру, является многоугольник площади S, то объем призмы вычисляется по формуле

Задача 13
Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния между ними равны 26 см, 25 см и 17 см. Найдите объем призмы.
Проведем сечение призмы плоскостью, перпендикулярной боковому ребру. Используя формулу Герона найдем площадь сечения: Полупериметр
см2. Тогда объем призмы равен см3.
Ответ: 3060 см3.

Задача 14
Основанием призмы является параллелограмм со сторонами 1, 2 и острым углом 30о. Боковые ребра равны 3 и составляют с плоскостью основания угол 45о. Найдите объем призмы.
Проведем высоту призмы.
Рассмотрим треугольник АВН, он прямоугольный с углов 45о, значит является равнобедренным ВН = АН, тогда высоту ВН (обозначим h, ВН = АН = h) найдем по теореме Пифагора:
30о
. В основании параллелограмм, в котором известны две стороны и угол между ними, тогда его площадь: кв. ед. куб. ед.
Ответ: куб. ед.

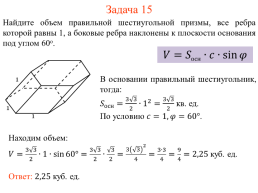
Задача 15
Найдите объем правильной шестиугольной призмы, все ребра которой равны 1, а боковые ребра наклонены к плоскости основания под углом 60о.
В основании правильный шестиугольник, тогда: кв. ед. По условию .
Находим объем: куб. ед.
Ответ: куб. ед.

Задачи для самостоятельного решения
1) Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.