Презентация - Математика красоты в русском деревянном зодчестве (на примере старо-вознесенской Тихвинской церкви г. Торжка)

Министерство промышленности и торговли Тверской области ГБП ОУ «Торжокский государственный промышленно-гуманитарный
МАТЕМАТИКА КРАСОТЫ В РУССКОМ ДЕРЕВЯННОМ ЗОДЧЕСТВЕ (НА ПРИМЕРЕ СТАРО-ВОЗНЕСЕНСКОЙ ТИХВИНСКОЙ ЦЕРКВИ г. ТОРЖКА)  ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ
Выполнил: студент 1 курса Эгля Роман Преподаватель: Т.Б. Коронкова

Цель проекта: Исследование пропорций Старо-Вознесенской Тихвинской церкви в Торжке.
Объект исследования: пропорции как основа гармонии в архитектуре. Предмет исследования: пропорции Старо-Вознесенской Тихвинской церкви в Торжке. Гипотеза: Старо-Вознесенская Тихвинская церковь в г. Торжке является примером использования пропорций в архитектуре. Задачи проекта: уточнить исторические факты о предмете исследования; изучить сведения о математических законах, определяющих красоту архитектуры; выбрать метод измерений, выполнить измерения и расчеты; обобщить полученные результаты и сделать выводы.

Историческая справка
Храм впервые упоминается в «Писцовой книге» Потапа Нарбекова в 1625 году. Вначале храм представлял собой сруб с двускатной крышей и одной главкой. В 1653 году на месте этого храма был возведён новый, который стал основой современного здания.

Архитектурный стиль церкви – ярусные храмы. На высоком четверикѐ храма поставлены три постепенно уменьшающихся восьмигранных яруса. Такую конструкцию называли «восьмерѝк на четверикѐ». Венчает постройку луковичная главка на высоком барабане.

Церковь особенно величественно смотрится на фоне города, так как стоит на возвышенном берегу реки Тверцы.

Математические законы красоты в архитектуре
В античную эпоху были выработаны критерии прекрасного, такие как: категория меры, включающая в себя как составные элементы понятия симметрии, пропорциональности и ритма, и категория гармонии

Симметрия и асимметрия
Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность. Примером удивительного сочетания симметрии и асимметрии является Покровский собор (храм Василия блаженного) на Красной площади в Москве.

Пропорция
В качестве меры соотношения симметричного и асимметричного часто и выступает пропорция. Золотая пропорция (золотое сечение) – это деление отрезка на две неравные части, при котором меньшая из них так относится к большей, как последняя ко всей длине отрезка.

Ритм и гармония
Ритм – закономерное повторение и чередование однородных элементов или групп форм. Гармония означает соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое

Геометрическая прогрессия – основа гармонии
Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение, т. е. архитектурное "целое" а и его части а1, а2, а3, а4, ... должны находиться в одинаковых отношениях:   т. е. "целое" а и его части a1, а2, а3, ... должны образовывать геометрическую прогрессию: а = а1р, а1 = а2р, а2 = а3р, … или , где n – порядковый номер члена прогрессии, b1 – первый член последовательности, p – знаменатель геометрической прогрессии.

Геометрическая прогрессия – основа гармонии
Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение, т. е. архитектурное "целое" а и его части а1, а2, а3, а4, ... должны находиться в одинаковых отношениях:   т. е. "целое" а и его части a1, а2, а3, ... должны образовывать геометрическую прогрессию: а = а1р, а1 = а2р, а2 = а3р, … или , где n – порядковый номер члена прогрессии, b1 – первый член последовательности, p – знаменатель геометрической прогрессии.

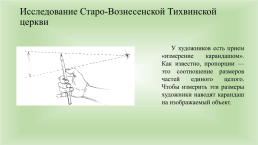
Исследование Старо-Вознесенской Тихвинской церкви
У художников есть прием «измерение карандашом». Как известно, пропорции — это соотношение размеров частей единого целого. Чтобы измерить эти размеры художники наводят карандаш на изображаемый объект.

Если использовать этот же прием, но в руке держать линейку, то можно получить размеры в миллиметрах отдельных частей здания. При этом имеет смысл совмещать нулевую отметку с верхней точкой измеряемого отрезка, а палец удерживать на уровни линии отсчета.

Полученные результаты не будут обеспечивать абсолютной точности, но все же позволят получить представления о пропорциях здания. Условием при этом должно быть достаточно большое расстояние от объекта измерения, чтобы уменьшить оптические искажения. Измерения были выполнены на расстоянии 80 м от церкви. На эскизе размеры в мм.

Результаты обработки и анализа результатов
Соотношение размеров восьмерико̀в
Ярусы.Соотношение высот.Соотношение ширины граней.Соотношение диаметров вписанных окружностей
а4/а3.32 / 34 = 0,9.10 / 11 = 0,9.25 / 28 = 0,9
а3/а2.34 / 36 = 0,9.11 / 12 = 0,9.28 / 25 = 0,9
Соотношение граней восьмериков и радиусов вписанных окружностей:

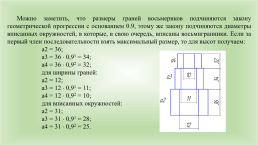
Можно заметить, что размеры граней восьмериков подчиняются закону геометрической прогрессии с основанием 0.9, этому же закону подчиняются диаметры вписанных окружностей, в которые, в свою очередь, вписаны восьмигранники. Если за первый член последовательности взять максимальный размер, то для высот получаем: а2 = 36; а3 = 36  0,91 = 34; а4 = 36  0,92 = 32; для ширины граней: а2 = 12; а3 = 12  0,91 = 11; а4 = 12  0,92 = 10; для вписанных окружностей: а2 = 31; а3 = 31  0,91 = 28; а4 = 31  0,92 = 25.

В архитектуре основной части здания наблюдается симметрия, так как используются в плане такие фигуры как квадрат и восьмигранник, центры которых совмещены. Это позволяет воспринимать здание как завершенную надежную конструкцию. Использование повторяющихся элементов (восьмерико̀в) придает конструкции ритмичность, позволяет создать эффект устремленности в небо, в вечность.

Вывод по результатам исследования
Несмотря на неточности выбранного способа измерений пропорций, исследования пропорций церкви показали, что они подчиняются законам математики и законам красоты (симметрии, пропорциональности, ритма и гармонии). Гипотеза исследования подтвердилась.

В презентации использованы авторские фотографии, а также фотографии с интернет-ресурсов:
Голубев А. Снято 8.06.2020. URL: https://sobory.ru/photo/410164. Старо-Вознесенская Тихвинская церковь. URL: https://autotravel.ru/phalbum/91567/155.jpg. Торжокский Тихвинский храм. Открытая православная энциклопедия. URL: https://drevo-info.ru/articles/13676908.html. Турбаев Р. Завершение. Снято 5.01.2016. URL: https://sobory.ru/photo/437332.

СПАСИБО ЗА ВНИМАНИЕ!