Презентация - Красота математики во Фракталах

Красота математики во фракталах
Подготовила: ученица 11 класса МКОУ СОШ №6 с.Нагусткое Теунаева Аиша. Преподаватель: Гаспарян И.В.

Содержание:
Цель презентации: познакомиться с понятием "фракталы" и показать всю их красоту.   Гипотеза: всё, что окружает нас является фракталами. Что такое фракталы? Свойства фракталов. История открытия фракталов. Типы фракталов:                 А) Геометрические фракталы:                              1) Снежинка Коха;                              2) Треугольник Серпинмкого;                              3) Драконова ломаная;             Б) Алгебраические фракталы:                               1) Отдельные проекции множества Мандельброта.  Интересные факты.    Заключение.

Что такое фракталы?
Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.

Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если рассмотреть небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах можно увидеть одинаково сложную картину. Является самоподобным или приближённо самоподобным. Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую
Свойства фракталов

История открытия фракталов
Первые идеи фрактальной геометрии возникли в XIX веке. Георг Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии. На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии. Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек. А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость.

Типы Фракталов
геометрические фракталы алгебраические фракталы системы итерируемых функций стохастические фракталы

Геометрические фракталы
Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется «затравка» - набор отрезков, на основании которых будет строиться фрактал. Далее к ней применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фрактал.

Снежинка коха
n=1
Из геометрических фракталов очень интересным и довольно знаменитым является снежинка Коха. Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длина кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны.
n=2
n=3
n=4

Треугольник Серпинского
Для построения серпиского треугольника из центра треугольника мысленно вырежем кусок треугольной формы, который своими вершинами будет упираться в середины сторон исходного треугольника. Повторим эту же процедуру для трех образовавшихся треугольников (за исключением центрального) и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием. Для построения коврика Серпинского нарисуем на листе бумаги равносторонний треугольник. Соединим прямыми линиями середины сторон треугольника, внутри него получается четыре треугольника. Средний вырежем. То же проделаем в трех угловых треугольниках. Получатся четыре отверстия и девять маленьких треугольников. Каждый подвергнем той же операции. По теории, конца этому процессу не будет, в треугольнике не останется живого места, но и на части он не распадется – получится «сыр», состоящий из одних дырок. Именно так и устроен наш мир. Все в нем до бесконечности дробится на части, приблизительно подобные целому, ибо реальность фрактальна. Подобие легко распознается, ведь его образы витают всюду. Бесконечное дробление и подобие мельчайших частей целому – это есть принцип «устройства» природы. В настоящие время придумано множество искусственных моделей, иллюстрирующих этот принцип.

Драконова ломаная.
Драконова ломаная относится к классу самоподобных геометрических структур. Ломаная нулевого порядка представляет собой просто прямой угол. Изображение фигуры каждого следующего порядка строится путем рекурсивных замен каждого из отрезков фигуры младшего порядка на два отрезка, сложенных также в виде прямого угла. При этом каждый первый угол оказывается «вывернутым» наружу, а каждый второй - вовнутрь. Несмотря на внешнюю простоту, построение драконовой ломаной - увлекательная алгоритмическая задачка, решение которой может потребовать от вас определенных мыслительных усилий. На рисунке изображен вполне взрослый «дракон» десятого порядка.

Алгебраический фрактал
Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов - многократный расчет функции. Расчет продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. На рисунке, изображающем множество Мандельброта, взят небольшой участок и увеличен до размеров всего экрана (как в микроскоп). Что же мы видим? Проявление самоподобности. Не точной самоподобности, но близкой, и с ней мы будем сталкиваться постоянно, увеличивая части нашего фрактала больше и больше. До каких же пор мы можем увеличивать наше множество? Так вот если мы увеличим его до предела вычислительной мощности компьютеров, то покроем площадь равную площади солнечной системы вплоть до Сатурна.

Знаменитое множество Мандельброта было описано в 1905 году Пьером Фату, но увидеть его ученый начала столетия не мог: вручную сделать необходимое число вычислений было физически невозможно. Для этого потребовались компьютеры, которыми воспользовался Бенуа Мандельброт для изучения уже описанного, но еще толком не исследованного.

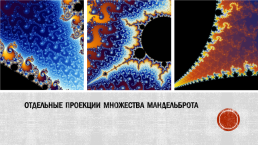
Отдельные проекции множества Мандельброта

Интерсные факты
ЭНЕРГИЯ ИСЦЕЛЕНИЯ И САКРАЛЬНАЯ ГЕОМЕТРИЯ Сакральная геометрия включает в себя использование геометрических узоров и коэффициенты, видны некоторые строительные блоки жизни и что приобрели значительную популярность среди New Age мыслителей. Применительно к некоторым фракталы, как спирали, деревья и замысловатые треугольник фигуры, эти показатели считаются гармонизировать энергии тела и помочь с некоторыми энергии исцеления практики. Один из самых популярных показателей сакральной геометрии является золотой пропорции (1.61803399), найдены во многих местах во Вселенной и всей природы, в том числе галактик, ракушки и растения.               КРАСОТА ФРАКТАЛОВ Один из самых увлекательных фактов о фрактальных фигур является их пленительной красотой. Возможность изображать потрясающие графические изображения ее наименьшее возможные детали, с повторяющейся формы, яркие цветовые сочетания и замысловатые, но природные сложности, фракталы представляют художественные и элегантный сторона математики, их изображения, обычно используется в передовых 3D иллюстрации и графика.

Заключение
В работе приведены далеко не все примеры человеческих знаний, где фракталы нашли своё применение. Хочу подметить, что со времени возникновения теории прошло не более трети века, но за это время фракталы для многих исследователей стали новым источником для научных открытий. Ведь именно благодаря теории фракталов ученым удалось объяснить эволюцию галактик и развитие клетки, возникновение гор и образование облаков.

Интернет ресурсы
https://allwomenstalk.com/ru/5509214a77f1343dc312dd4f/ https://ru.wikipedia.org/wiki/Фрактал https://infourok.ru/material.html?mid=85283 https://pandia.ru/text/79/026/16103.php

Спасибо за внимание.