Презентация - Урок математики в 6 классе по теме «Пропорции»

Урок математики в 6 классе по теме: «Пропорции»

Отгадай ребус

Тема урока: Пропорции
Цель урока: Узнать, что такое пропорции Как называются члены пропорции Вывести основное свойство пропорции Познакомиться с видами пропорций

Уже древние греки использовали законы пропорции для строительства зданий. Для строительства фасада Парфенона, храма в Афинах использована « божественная пропорция». Знания, полученные на этом уроке, помогут решать задачи с помощью пропорций. Позже задачи с помощью пропорций вы будете решать по химии, физике, геометрии.
Что же такое пропорция?

Из отношений выберите равные:
20 : 5 3 : 15 10 : 4 7 : 3,5 3 : 0,5 2 : 10 16 : 4 6 : 1

Одинаковые отношения запишем в виде равенства:
20 : 5 = 16 : 4 3 : 15 = 2 : 10 3 : 0,5 = 6 : 1

Равенство двух отношений называют пропорцией.
Слово «пропорция» (от латинского proportio) означает «соразмерность», «определенное соотношение частей между собой»

С помощью букв пропорцию можно записать так:
а : в = с : d
КРАЙНИЕ ЧЛЕНЫ
СРЕДНИЕ ЧЛЕНЫ

Пропорция 20 : 5 = 16 : 4 3 : 15 = 2 : 10 3 : 0,5 = 6 : 1 а : в = с : d
Крайние члены
Средние члены
Произведение крайних членов
Произведение средних членов
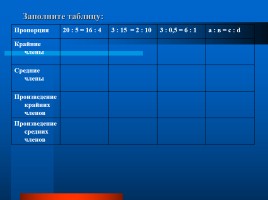
Заполните таблицу:

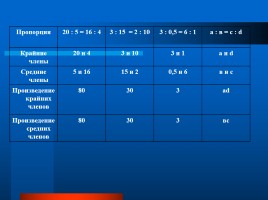
Пропорция 20 : 5 = 16 : 4 3 : 15 = 2 : 10 3 : 0,5 = 6 : 1 а : в = с : d
Крайние члены 20 и 4 3 и 10 3 и 1 а и d
Средние члены 5 и 16 15 и 2 0,5 и 6 в и с
Произведение крайних членов 80 30 3 ad
Произведение средних членов 80 30 3 вс

Основное свойство пропорции:
Если а : в = c : d, то а·d = в·с В верной пропорции произведение крайних членов равно произведению средних. Если а·d = в·с, то а : в = c : d Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.

Используя верное равенство 15 · 8 = 40 · 3, составьте 4 верные пропорции.
15 : 3 = 40 : 8 3 : 15 = 8 : 40 3 : 8 = 15 : 40 40 : 15 = 8 : 3