Презентация - Метрологические основы, методы и техника измерений физических величин. Лекция № 1. Введение
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 95%
- Слайдов: 195
- Просмотров: 1420
- Скачиваний: 72
- Размер: 11.71 MB
- Класс: 7
- Формат: ppt / pptx
Примеры похожих презентаций
 Основные методы коррекции фигуры с помощью физических упражнений
Основные методы коррекции фигуры с помощью физических упражнений Физические величины и их измерение
Физические величины и их измерение Основные методы коррекции фигуры с помощью физических упражнений
Основные методы коррекции фигуры с помощью физических упражнений Техника безопасности на уроках физической культуры
Техника безопасности на уроках физической культуры Единицы различных физических величин
Единицы различных физических величин Основы техники северной ходьбы
Основы техники северной ходьбы Методы изучения живой природы: измерение
Методы изучения живой природы: измерение
Слайды и текст этой онлайн презентации
Слайд 1

Метрологические основы, методы и техника измерений физических величин
Лекция № 1. Введение
Преподаватель: Войнов Виктор Сергеевич
Лекция № 1. Введение
Преподаватель: Войнов Виктор Сергеевич
Слайд 2

Структура курса
Лекции (8) Контрольные работы (2) Лабораторные работы (6) Зачет
Лекции (8) Контрольные работы (2) Лабораторные работы (6) Зачет
Слайд 3

Литература
Приборы и методы измерения электрических величин/ Э.Г. Атамелян, 3-е изд., М.:Дрофа, 2005 Основы метрологии и электрические измерения / под редакцией Е.М. Душина, Л. Энергоатомиздат, 1987 Метрология в электрических измерениях, С.П. Санников, Екатеринбург, 2011 ГОСТ Р 8.736-2011 Измерения прямые многократные
Приборы и методы измерения электрических величин/ Э.Г. Атамелян, 3-е изд., М.:Дрофа, 2005 Основы метрологии и электрические измерения / под редакцией Е.М. Душина, Л. Энергоатомиздат, 1987 Метрология в электрических измерениях, С.П. Санников, Екатеринбург, 2011 ГОСТ Р 8.736-2011 Измерения прямые многократные
Слайд 4

1.1 Основные определения и термины
Физическая величина (ФВ) Измеряемая ФВ (Размер, значение, числовое значение, единица измерения) Истинное и действительное значение ФВ Измерение ФВ (результат измерения, измерительная задача)
Физическая величина (ФВ) Измеряемая ФВ (Размер, значение, числовое значение, единица измерения) Истинное и действительное значение ФВ Измерение ФВ (результат измерения, измерительная задача)
Слайд 5

1.1 Основные определения и термины
Абсолютная погрешность.Относительная погрешность
Δх = х — А.δ = Δх / х
Отклонение результата измерения измеряемой величины х от истинного / действительного значения ФВ А..Погрешность измерения, выраженная отношением абсолютной погрешности Δх к измеряемой величине х.
Точность результата измерений численно равна величине, обратной модулю относительной погрешности.
Абсолютная погрешность.Относительная погрешность
Δх = х — А.δ = Δх / х
Отклонение результата измерения измеряемой величины х от истинного / действительного значения ФВ А..Погрешность измерения, выраженная отношением абсолютной погрешности Δх к измеряемой величине х.
Точность результата измерений численно равна величине, обратной модулю относительной погрешности.
Слайд 6
1.1 Основные определения и термины
СРЕДСТВО
МЕТОД
ПРИНЦИП
СРЕДСТВО
МЕТОД
ПРИНЦИП
Слайд 7
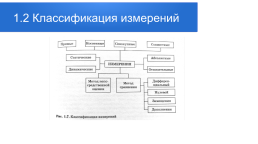
1.2 Классификация измерений
Слайд 8
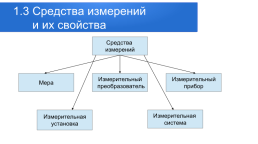
1.3 Средства измерений и их свойства
Средства измерений
Мера
Измерительный преобразователь
Измерительный прибор
Измерительная установка
Измерительная система
Средства измерений
Мера
Измерительный преобразователь
Измерительный прибор
Измерительная установка
Измерительная система
Слайд 9

1.3 Средства измерений и их свойства
Средство измерения(СИ) — техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее или хранящее единицу ФВ, размер которой принимают неизменным,в течение установленного интервала времени. Мера — СИ, предназначенное для воспроизведения или хранения ФВ одного или нескольких заданных размеров, значения которых выражены в установленных единицах с необходимой точностью.
Средство измерения(СИ) — техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее или хранящее единицу ФВ, размер которой принимают неизменным,в течение установленного интервала времени. Мера — СИ, предназначенное для воспроизведения или хранения ФВ одного или нескольких заданных размеров, значения которых выражены в установленных единицах с необходимой точностью.
Слайд 10

1.3 Средства измерений и их свойства
Измерительный преобразователь (ИП) - техническое средство с нормированными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину, удобную для обработки, хранения, передачи и дальнейшего преобразования.
Измерительный преобразователь (ИП) - техническое средство с нормированными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину, удобную для обработки, хранения, передачи и дальнейшего преобразования.
Слайд 11

1.3 Средства измерений и их свойства
Измерительный прибор — средство измерений, предназначенное для получения значений измеряемой ФВ в установленном диапазоне Измерительная установка — совокупность функционально объединенных мер, измерительных преобразователей, измерительных приборов и других устройств Измерительная система - совокупность функционально объединенных мер, ИП, измерительных приборов, установок и других технических средств, размещенных в разных точках контролируемого объекта с целью измерения одной или нескольких ФВ, свойственных этому объекту и выработки сигналов в различных целях.
Измерительный прибор — средство измерений, предназначенное для получения значений измеряемой ФВ в установленном диапазоне Измерительная установка — совокупность функционально объединенных мер, измерительных преобразователей, измерительных приборов и других устройств Измерительная система - совокупность функционально объединенных мер, ИП, измерительных приборов, установок и других технических средств, размещенных в разных точках контролируемого объекта с целью измерения одной или нескольких ФВ, свойственных этому объекту и выработки сигналов в различных целях.
Слайд 12

1.4 Классификация электронных приборов
Классификация классификаций: В зависимости от физических явлений По характеру и виду измеряемых величин По виду выдаваемой информации По схеме преобразования По способу выдачи измерительной информации По характеру установки По характеру измерений и виду измеряемых величин
Классификация классификаций: В зависимости от физических явлений По характеру и виду измеряемых величин По виду выдаваемой информации По схеме преобразования По способу выдачи измерительной информации По характеру установки По характеру измерений и виду измеряемых величин
Слайд 13
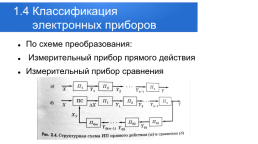
1.4 Классификация электронных приборов
По схеме преобразования: Измерительный прибор прямого действия Измерительный прибор сравнения
По схеме преобразования: Измерительный прибор прямого действия Измерительный прибор сравнения
Слайд 14

1.5 Метрологические характеристики СИ
Градуировочная характеристика — зависимость между х на входе и у на выходе: у = f(x)
Связанные определения: Чувствительность Порог чувствительности Шкала прибора Числовая отметка шкалы Цена деления шкалы
Градуировочная характеристика — зависимость между х на входе и у на выходе: у = f(x)
Связанные определения: Чувствительность Порог чувствительности Шкала прибора Числовая отметка шкалы Цена деления шкалы
Слайд 15

1.5 Метрологические характеристики СИ
Чувствительность прибора — свойство, определяемое отношением изменения выходного сигнала прибора к вызывающему изменению измеряемой величины S = ΔY / ΔX Порог чувствительности — характеристика прибора в виде наименьшего значения изменения величины, начиная с которого может осуществляться ее измерение данным прибором Шкала прибора, цена деления шкалы Динамический диапазон -
Чувствительность прибора — свойство, определяемое отношением изменения выходного сигнала прибора к вызывающему изменению измеряемой величины S = ΔY / ΔX Порог чувствительности — характеристика прибора в виде наименьшего значения изменения величины, начиная с которого может осуществляться ее измерение данным прибором Шкала прибора, цена деления шкалы Динамический диапазон -
Слайд 16

1.6 Классификация погрешностей
Инструментальная погрешность измерения — составляющая погрешности измерений, обусловленная свойствами применяемых средств измерений Основная Дополнительная Обусловленная взаимодействием прибора и объекта измерения Динамическая
Инструментальная погрешность измерения — составляющая погрешности измерений, обусловленная свойствами применяемых средств измерений Основная Дополнительная Обусловленная взаимодействием прибора и объекта измерения Динамическая
Слайд 17

1.6 Классификация погрешностей
Основная погрешность — погрешность СИ, применяемого в нормальных условиях.
По способу числового выражения:.По характеру влияния на функцию преобразования:.По источнику происхождения:
Абсолютная.Аддитивная.Систематическая
Относительная.Мультипликативная.Случайная
Приведенная..Промах
Основная погрешность — погрешность СИ, применяемого в нормальных условиях.
По способу числового выражения:.По характеру влияния на функцию преобразования:.По источнику происхождения:
Абсолютная.Аддитивная.Систематическая
Относительная.Мультипликативная.Случайная
Приведенная..Промах
Слайд 18

1.6 Классификация погрешностей
Слайд 19

1.6 Классификация погрешностей
Слайд 20
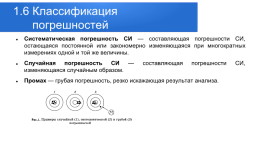
1.6 Классификация погрешностей
Систематическая погрешность СИ — составляющая погрешности СИ, остающаяся постоянной или закономерно изменяющаяся при многократных измерениях одной и той же величины. Случайная погрешность СИ — составляющая погрешности СИ, изменяющаяся случайным образом. Промах — грубая погрешность, резко искажающая результат анализа.
Систематическая погрешность СИ — составляющая погрешности СИ, остающаяся постоянной или закономерно изменяющаяся при многократных измерениях одной и той же величины. Случайная погрешность СИ — составляющая погрешности СИ, изменяющаяся случайным образом. Промах — грубая погрешность, резко искажающая результат анализа.
Слайд 21

1.6 Классификация погрешностей
Дополнительная погрешность — обусловлена реакцией СИ на изменение внешних влияющих величин и неинформативных параметров входного сигнала Погрешность, обусловленная взаимодействием СИ и объекта измерения : подключение СИ к объекту во многих случаях приводит к изменению значения измеряемой ФВ относительно того значения, которое она имела до подключения.
Дополнительная погрешность — обусловлена реакцией СИ на изменение внешних влияющих величин и неинформативных параметров входного сигнала Погрешность, обусловленная взаимодействием СИ и объекта измерения : подключение СИ к объекту во многих случаях приводит к изменению значения измеряемой ФВ относительно того значения, которое она имела до подключения.
Слайд 22

1.6 Классификация погрешностей
Динамическая погрешность СИ — погрешность, возникающая при измерении изменяющейся в процессе измерения ФВ. Для описания СИ в динамическом режиме(подробнее в лекции 5) используются: Полная динамическая характеристика Частная динамическая характеристика
Динамическая погрешность СИ — погрешность, возникающая при измерении изменяющейся в процессе измерения ФВ. Для описания СИ в динамическом режиме(подробнее в лекции 5) используются: Полная динамическая характеристика Частная динамическая характеристика
Слайд 23

1.7 Класс точности и нормирование погрешностей
Класс точности — обобщенная характеристика данного типа СИ, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности дает судить о том, в каких пределах находится погрешность измерений одного типа. Предел допускаемой погрешности СИ представляет собой наибольшее значение погрешности, устанавливаемое нормативным документом, при котором СИ еще остается годным к применению.
Класс точности — обобщенная характеристика данного типа СИ, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности дает судить о том, в каких пределах находится погрешность измерений одного типа. Предел допускаемой погрешности СИ представляет собой наибольшее значение погрешности, устанавливаемое нормативным документом, при котором СИ еще остается годным к применению.
Слайд 24

1.7 Класс точности и нормирование погрешностей
Нормирование погрешности Если аддитивная преобладает над мультипликативной: 1)Нормируем абсолютную погрешность γ = Δ / Xn = ±p 2)Нормирующее значение Xn принимается равным Конечному значению шкалы прибора, если нулевая отметка на краю или вне шкалы Номинальному значению, если прибор измеряет номинальные значения Арифметической сумме конечных значений диапазона измерений Длине шкалы, если шкала резко нелинейная
Нормирование погрешности Если аддитивная преобладает над мультипликативной: 1)Нормируем абсолютную погрешность γ = Δ / Xn = ±p 2)Нормирующее значение Xn принимается равным Конечному значению шкалы прибора, если нулевая отметка на краю или вне шкалы Номинальному значению, если прибор измеряет номинальные значения Арифметической сумме конечных значений диапазона измерений Длине шкалы, если шкала резко нелинейная
Слайд 25

1.7 Класс точности и нормирование погрешностей
Нормирование погрешности Если мультипликативная преобладает над аддитивной: Нормируем предел допускаемой относительной погрешности: δ = Δ / х = ± q Для СИ с мультипликативной и аддитивной погрешностями нормируется предел допускаемой относительной погрешности.
Нормирование погрешности Если мультипликативная преобладает над аддитивной: Нормируем предел допускаемой относительной погрешности: δ = Δ / х = ± q Для СИ с мультипликативной и аддитивной погрешностями нормируется предел допускаемой относительной погрешности.
Слайд 26

1.7 Класс точности и нормирование погрешностей
Примеры шкал приборов с разными классами точности
Пример расчета класса точности
Примеры шкал приборов с разными классами точности
Пример расчета класса точности
Слайд 27

Рекомендуемые задачи
Санников, задача №1
Санников, задача №1
Слайд 28

Метрологические основы, методы и техника измерений физических величин
Лекция № 2. Введение в теорию сигналов
Преподаватель: Войнов Виктор Сергеевич
Лекция № 2. Введение в теорию сигналов
Преподаватель: Войнов Виктор Сергеевич
Слайд 29

2.0 Введение в теорию сигналов
Сигнал — зависимость некоторой электрической величины U от времени t. В эту зависимость помимо t могут входить и другие величины, которые называют параметрами сигнала. По способу представления на временной оси различают Аналоговые Дискретные Квантованные Цифровые
Сигнал — зависимость некоторой электрической величины U от времени t. В эту зависимость помимо t могут входить и другие величины, которые называют параметрами сигнала. По способу представления на временной оси различают Аналоговые Дискретные Квантованные Цифровые
Слайд 30
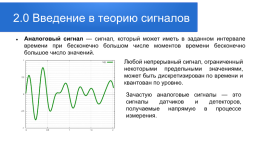
2.0 Введение в теорию сигналов
Аналоговый сигнал — сигнал, который может иметь в заданном интервале времени при бесконечно большом числе моментов времени бесконечно большое число значений.
Любой непрерывный сигнал, ограниченный некоторыми предельными значениями, может быть дискретизирован по времени и квантован по уровню.
Зачастую аналоговые сигналы — это сигналы датчиков и детекторов, получаемые напрямую в процессе измерения.
Аналоговый сигнал — сигнал, который может иметь в заданном интервале времени при бесконечно большом числе моментов времени бесконечно большое число значений.
Любой непрерывный сигнал, ограниченный некоторыми предельными значениями, может быть дискретизирован по времени и квантован по уровню.
Зачастую аналоговые сигналы — это сигналы датчиков и детекторов, получаемые напрямую в процессе измерения.
Слайд 31
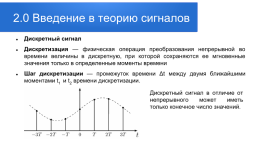
2.0 Введение в теорию сигналов
Дискретный сигнал Дискретизация — физическая операция преобразования непрерывной во времени величины в дискретную, при которой сохраняются ее мгновенные значения только в определенные моменты времени Шаг дискретизации — промежуток времени Δt между двумя ближайшими моментами t1 и t2 времени дискретизации.
Дискретный сигнал в отличие от непрерывного может иметь только конечное число значений.
Дискретный сигнал Дискретизация — физическая операция преобразования непрерывной во времени величины в дискретную, при которой сохраняются ее мгновенные значения только в определенные моменты времени Шаг дискретизации — промежуток времени Δt между двумя ближайшими моментами t1 и t2 времени дискретизации.
Дискретный сигнал в отличие от непрерывного может иметь только конечное число значений.
Слайд 32
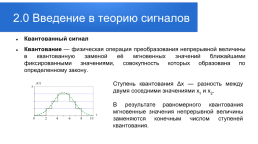
2.0 Введение в теорию сигналов
Квантованный сигнал Квантование — физическая операция преобразования непрерывной величины в квантованную заменой её мгновенных значений ближайшими фиксированными значениями, совокупность которых образована по определенному закону.
Ступень квантования Δх — разность между двумя соседними значениями x1 и x2. В результате равномерного квантования мгновенные значения непрерывной величины заменяются конечным числом ступеней квантования.
Квантованный сигнал Квантование — физическая операция преобразования непрерывной величины в квантованную заменой её мгновенных значений ближайшими фиксированными значениями, совокупность которых образована по определенному закону.
Ступень квантования Δх — разность между двумя соседними значениями x1 и x2. В результате равномерного квантования мгновенные значения непрерывной величины заменяются конечным числом ступеней квантования.
Слайд 33

2.0 Введение в теорию сигналов
Цифровой сигнал Дискретный по времени и квантованный по уровню сигнал. Квантованные значения сигнала заменяются числами, реализованными в двоичном коде.
Возможный диапазон изменения мгновенных значений аналогового сигнала разбивается (квантуется) на 2N равных частей, где N — разрядность двоичного числа На каждом интервале дискретизации квантованная но уровню величина преобразуется в последовательность импульсов, отражающих двоичное число. Для этого интервал дискретизации разбивается на N равных частей (тактов).
Цифровой сигнал Дискретный по времени и квантованный по уровню сигнал. Квантованные значения сигнала заменяются числами, реализованными в двоичном коде.
Возможный диапазон изменения мгновенных значений аналогового сигнала разбивается (квантуется) на 2N равных частей, где N — разрядность двоичного числа На каждом интервале дискретизации квантованная но уровню величина преобразуется в последовательность импульсов, отражающих двоичное число. Для этого интервал дискретизации разбивается на N равных частей (тактов).
Слайд 34
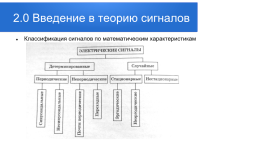
2.0 Введение в теорию сигналов
Классификация сигналов по математическим характеристикам
Классификация сигналов по математическим характеристикам
Слайд 35
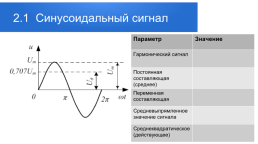
2.1 Cинусоидальный сигнал
Параметр.Значение
Гармонический сигнал.
Постоянная составляющая (среднее).
Переменная составляющая.
Средневыпрямленное значение сигнала.
Среднеквадратическое (действующее).
Параметр.Значение
Гармонический сигнал.
Постоянная составляющая (среднее).
Переменная составляющая.
Средневыпрямленное значение сигнала.
Среднеквадратическое (действующее).
Слайд 36

2.1 Cинусоидальный сигнал
Слайд 37

2.2 Импульсный сигнал
Импульсные сигналы — детерминированные сигналы конечной энергии, существенно отличные от нуля в течение ограниченного интервала времени. Видеоимпульсы - однополярные импульсы тока или напряжения, которые могут быть положительной или отрицательной полярности относительно определенного уровня, принятого за нулевой. Скважность — параметр периодического прямоугольного импульса, характеризующий отношение периода повторения импульсов к длительности импульса D = T/tимп
Постоянная составляющая.
Среднеквадратическое (действующее).
Импульсные сигналы — детерминированные сигналы конечной энергии, существенно отличные от нуля в течение ограниченного интервала времени. Видеоимпульсы - однополярные импульсы тока или напряжения, которые могут быть положительной или отрицательной полярности относительно определенного уровня, принятого за нулевой. Скважность — параметр периодического прямоугольного импульса, характеризующий отношение периода повторения импульсов к длительности импульса D = T/tимп
Постоянная составляющая.
Среднеквадратическое (действующее).
Слайд 38
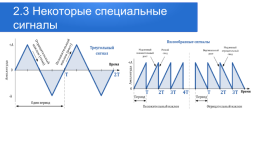
2.3 Некоторые специальные сигналы
Слайд 39

2.4 Случайные сигналы
Случайными называют сигналы, мгновенные значения которых принимают одно из множества возможных значений. Функция времени, описывающая случайный сигнал, называется выборочной функцией (или при конечном интервале — реализацией функции). Множество реализаций составляют совокупность, формирующую случайный сигнал. Полное описание случайных сигналов осуществляется с помощью ряда вероятностных характеристик, каждая из которых является усреднением либо по совокупности реализаций xk(t), либо усреднением по времени одной реализации. Результаты усреднений могут зависеть или не зависеть от времени и номера реализации. Стационарным называется сигнал, вероятностные характеристики которого не зависят от времени Эргодическим называется сигнал, вероятностные характеристики которого не зависят от номера реализации
Случайными называют сигналы, мгновенные значения которых принимают одно из множества возможных значений. Функция времени, описывающая случайный сигнал, называется выборочной функцией (или при конечном интервале — реализацией функции). Множество реализаций составляют совокупность, формирующую случайный сигнал. Полное описание случайных сигналов осуществляется с помощью ряда вероятностных характеристик, каждая из которых является усреднением либо по совокупности реализаций xk(t), либо усреднением по времени одной реализации. Результаты усреднений могут зависеть или не зависеть от времени и номера реализации. Стационарным называется сигнал, вероятностные характеристики которого не зависят от времени Эргодическим называется сигнал, вероятностные характеристики которого не зависят от номера реализации
Слайд 40
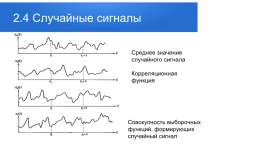
2.4 Случайные сигналы
Среднее значение случайного сигнала Корреляционная функция
Совокупность выборочных функций, формирующих случайный сигнал
Среднее значение случайного сигнала Корреляционная функция
Совокупность выборочных функций, формирующих случайный сигнал
Слайд 41
2.4 Случайные сигналы
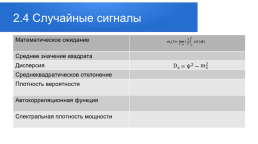
Математическое ожидание.
Среднее значение квадрата.
Дисперсия.
Среднеквадратическое отклонение.
Плотность вероятности.
Автокорреляционная функция.
Спектральная плотность мощности.
Математическое ожидание.
Среднее значение квадрата.
Дисперсия.
Среднеквадратическое отклонение.
Плотность вероятности.
Автокорреляционная функция.
Спектральная плотность мощности.
Слайд 42

2.5 Помехи и шумы
Помеха — сигнал, однородный с измерительным и действующий одновременно с ним. По месту возникновения помехи бывают внешние, внутренние, индустриальные По основным свойствам помехи делятся на флуктуационные, сосредоточенные и импульсные Шум — это беспорядочные колебания различной физической природы, отличающиеся сложностью спектра. Белый шум — спектр равномерный на всем протяжении частот Розовый шум — спектральная плотность убывает обратно пропорционально частоте Коричневый шум — спектральная плотность убывает обратно пропорционально квадрату частоты
Помеха — сигнал, однородный с измерительным и действующий одновременно с ним. По месту возникновения помехи бывают внешние, внутренние, индустриальные По основным свойствам помехи делятся на флуктуационные, сосредоточенные и импульсные Шум — это беспорядочные колебания различной физической природы, отличающиеся сложностью спектра. Белый шум — спектр равномерный на всем протяжении частот Розовый шум — спектральная плотность убывает обратно пропорционально частоте Коричневый шум — спектральная плотность убывает обратно пропорционально квадрату частоты
Слайд 43

2.6 Практическая реализация спектрального анализа
Сложный сигнал можно представить в виде ряда Фурье Среднеквадратическое значение сложного сигнала Основная характеристика сложных сигналов — их спектральная функция, дающая информацию об амплитудах и фазах отдельных гармоник. Спектральное разложение — представление непрерывных детерминированных сигналов в виде совокупности постоянной составляющей и суммы гармоник с кратным набором частот. Периодические сигналы состоят из гармоник, частоты которых кратны основной частоте сложного колебания Спектр — зависимость амплитуды или фазы гармоники сигнала от его частоты. Может быть сплошным или дискретным.
Сложный сигнал можно представить в виде ряда Фурье Среднеквадратическое значение сложного сигнала Основная характеристика сложных сигналов — их спектральная функция, дающая информацию об амплитудах и фазах отдельных гармоник. Спектральное разложение — представление непрерывных детерминированных сигналов в виде совокупности постоянной составляющей и суммы гармоник с кратным набором частот. Периодические сигналы состоят из гармоник, частоты которых кратны основной частоте сложного колебания Спектр — зависимость амплитуды или фазы гармоники сигнала от его частоты. Может быть сплошным или дискретным.
Слайд 44
2.6 Практическая реализация спектрального анализа
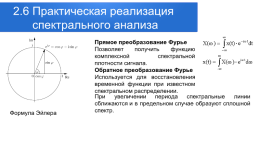
Прямое преобразование Фурье Позволяет получить функцию комплексной спектральной плотности сигнала. Обратное преобразование Фурье Используется для восстановления временной функции при известном спектральном распределении.
При увеличении периода спектральные линии сближаются и в предельном случае образуют сплошной спектр.
Формула Эйлера
Прямое преобразование Фурье Позволяет получить функцию комплексной спектральной плотности сигнала. Обратное преобразование Фурье Используется для восстановления временной функции при известном спектральном распределении.
При увеличении периода спектральные линии сближаются и в предельном случае образуют сплошной спектр.
Формула Эйлера
Слайд 45

2.6 Практическая реализация спектрального анализа
При дискретном преобразовании Фурье (ДПФ) аналоговый сигнал u(t) преобразуется в последовательность дискретных выборок uп(nΔt), следующих через интервал, равный шагу дискретизации Δt. Шаг дискретизации принимают равным периоду следования T0, n= 0… N-1 — число выборок. Функцию uп(nΔt) полагают периодической с периодом T = NT0.
При дискретном преобразовании Фурье (ДПФ) аналоговый сигнал u(t) преобразуется в последовательность дискретных выборок uп(nΔt), следующих через интервал, равный шагу дискретизации Δt. Шаг дискретизации принимают равным периоду следования T0, n= 0… N-1 — число выборок. Функцию uп(nΔt) полагают периодической с периодом T = NT0.
Слайд 46

Метрологические основы, методы и техника измерений физических величин
Лекция № 3. Измерение напряжения
Преподаватель: Войнов Виктор Сергеевич
Лекция № 3. Измерение напряжения
Преподаватель: Войнов Виктор Сергеевич
Слайд 47
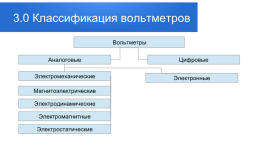
3.0 Классификация вольтметров
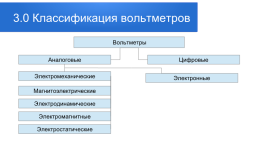
Вольтметры
Аналоговые
Цифровые
Электромеханические
Электронные
Магнитоэлектрические
Электродинамические
Электромагнитные
Электростатические
Вольтметры
Аналоговые
Цифровые
Электромеханические
Электронные
Магнитоэлектрические
Электродинамические
Электромагнитные
Электростатические
Слайд 48

3.0 Классификация вольтметров
Структурная схема аналогового электроизмерительного прибора (ЭИП)
Y
Х
Измерительная цепь
Измерительный механизм
Отсчетное устройство
α
Измерительная цепь обеспечивает преобразование измеряемой электрической величины Х в некоторую промежуточную величину Y, функционально связанную с измеряемой величиной. Измерительный механизм преобразует электромагнитную энергию в механическую, необходимую для отклонения подвижной части прибора на угол α относительно неподвижной, т. е.: α = f(Y) = F(X)
Структурная схема аналогового электроизмерительного прибора (ЭИП)
Y
Х
Измерительная цепь
Измерительный механизм
Отсчетное устройство
α
Измерительная цепь обеспечивает преобразование измеряемой электрической величины Х в некоторую промежуточную величину Y, функционально связанную с измеряемой величиной. Измерительный механизм преобразует электромагнитную энергию в механическую, необходимую для отклонения подвижной части прибора на угол α относительно неподвижной, т. е.: α = f(Y) = F(X)
Слайд 49

3.0 Классификация вольтметров
Дифференциальное уравнение моментов, описывающее работу ИМ имеет вид: На подвижную часть при ее движении действуют: Вращающий момент М Противодействующий момент Мα Момент успокоения Мусп
Дифференциальное уравнение моментов, описывающее работу ИМ имеет вид: На подвижную часть при ее движении действуют: Вращающий момент М Противодействующий момент Мα Момент успокоения Мусп
Слайд 50

3.1 Магнитоэлектрические ИМ
Принцип действия: взаимодействие магнитных полей катушки с током и магнитного потока постоянного магнита В воздушном зазоре между полюсными наконечниками магнита создается радиальное поле. Там е помещается катушка с измеряемым током. Ток пропускают через пружины, создающие противодействующий момент. Успокоение стрелки происходит за счет тормозного момента в каркасе рамки и подвесах индуцируемых токов, создающих вместе с постоянным магнитом тормозной магнитный момент. При изменении направления тока I меняется направление отклонения подвижной части ИМ. При включении ИМ в цепь переменного тока из-за инерционности подвижной части среднее значение вращающего момента за период будет равно нулю.
Принцип действия: взаимодействие магнитных полей катушки с током и магнитного потока постоянного магнита В воздушном зазоре между полюсными наконечниками магнита создается радиальное поле. Там е помещается катушка с измеряемым током. Ток пропускают через пружины, создающие противодействующий момент. Успокоение стрелки происходит за счет тормозного момента в каркасе рамки и подвесах индуцируемых токов, создающих вместе с постоянным магнитом тормозной магнитный момент. При изменении направления тока I меняется направление отклонения подвижной части ИМ. При включении ИМ в цепь переменного тока из-за инерционности подвижной части среднее значение вращающего момента за период будет равно нулю.
Слайд 51
3.1 Магнитоэлектрические ИМ
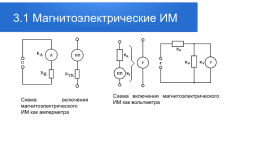
Схема включения магнитоэлектрического ИМ как вольтметра
Схема включения магнитоэлектрического ИМ как амперметра
Схема включения магнитоэлектрического ИМ как вольтметра
Схема включения магнитоэлектрического ИМ как амперметра
Слайд 52
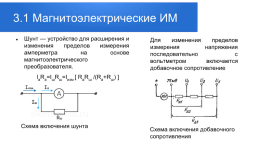
3.1 Магнитоэлектрические ИМ
Шунт — устройство для расширения и изменения пределов измерения амперметра на основе магнитоэлектрического преобразователя. IaRa=IшRш=Iизм [ RaRш /(Ra+Rш) ]
Для изменения пределов измерения напряжения последовательно с вольтметром включается добавочное сопротивление
Схема включения шунта
Схема включения добавочного сопротивления
Шунт — устройство для расширения и изменения пределов измерения амперметра на основе магнитоэлектрического преобразователя. IaRa=IшRш=Iизм [ RaRш /(Ra+Rш) ]
Для изменения пределов измерения напряжения последовательно с вольтметром включается добавочное сопротивление
Схема включения шунта
Схема включения добавочного сопротивления
Слайд 53

3.2 Электродинамические ИП
Принцип действия: взаимодействие магнитных потоков двух катушек с током. Пара катушек, соединенных последовательно, внутри которых — бескаркасная подвижная катушка на оси вращения. Для подвода тока и создания сопротивления вращению используют спиральные пружины. Энергия системы катушек: W = 0,5 I1^2L1+ 0,5 I2^2L2 +I1I2M M -взаимная индуктивность. Если потоки подвижной и неподвижной катушек совпадают то М>0,если нет, то М<0. Под действием вращающего момента подвижная катушка стремится занять такое положение, при котором направление ее МП совпадало бы с направлением МП неподвижной катушки. Она будет поворачиваться, пока вращающий и противодействующий моменты не сравняются друг с другом. Если подвижную и неподвижную катушки соединить последовательно, то итоговое отклонение будет пропорционально квадрату измеряемой электрической величины.
Принцип действия: взаимодействие магнитных потоков двух катушек с током. Пара катушек, соединенных последовательно, внутри которых — бескаркасная подвижная катушка на оси вращения. Для подвода тока и создания сопротивления вращению используют спиральные пружины. Энергия системы катушек: W = 0,5 I1^2L1+ 0,5 I2^2L2 +I1I2M M -взаимная индуктивность. Если потоки подвижной и неподвижной катушек совпадают то М>0,если нет, то М<0. Под действием вращающего момента подвижная катушка стремится занять такое положение, при котором направление ее МП совпадало бы с направлением МП неподвижной катушки. Она будет поворачиваться, пока вращающий и противодействующий моменты не сравняются друг с другом. Если подвижную и неподвижную катушки соединить последовательно, то итоговое отклонение будет пропорционально квадрату измеряемой электрической величины.
Слайд 54

3.3 Электромагнитные ИП
Принцип действия: втягивание парамегнетика в область сильного ЭМ поля. При прохождении по неподвижной плоской катушке измеряемого тока возникает магнитное поле, которое, воздействуя на лепесток 2, стремится расположить его так, чтобы энергия магнитного поля была наибольшей, т. е. втянуть лепесток внутрь катушки. Вращающий момент Шкала прибора квадратична, поэтому она в начале сжата, а в конце растянута.
Принцип действия: втягивание парамегнетика в область сильного ЭМ поля. При прохождении по неподвижной плоской катушке измеряемого тока возникает магнитное поле, которое, воздействуя на лепесток 2, стремится расположить его так, чтобы энергия магнитного поля была наибольшей, т. е. втянуть лепесток внутрь катушки. Вращающий момент Шкала прибора квадратична, поэтому она в начале сжата, а в конце растянута.
Слайд 55
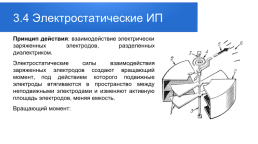
3.4 Электростатические ИП
Принцип действия: взаимодействие электрически заряженных электродов, разделенных диэлектриком. Электростатические силы взаимодействия заряженных электродов создают вращающий момент, под действием которого подвижные электроды втягиваются в пространство между неподвижными электродами и изменяют активную площадь электродов, меняя емкость. Вращающий момент:
Принцип действия: взаимодействие электрически заряженных электродов, разделенных диэлектриком. Электростатические силы взаимодействия заряженных электродов создают вращающий момент, под действием которого подвижные электроды втягиваются в пространство между неподвижными электродами и изменяют активную площадь электродов, меняя емкость. Вращающий момент:
Слайд 56
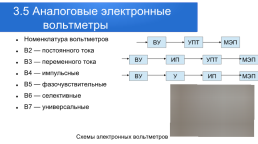
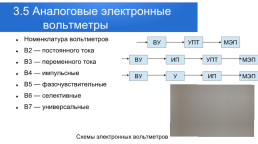
3.5 Аналоговые электронные вольтметры
Номенклатура вольтметров В2 — постоянного тока В3 — переменного тока В4 — импульсные В5 — фазочувствительные В6 — селективные В7 — универсальные
ВУ
УПТ
МЭП
ВУ
ИП
УПТ
МЭП
ВУ
У
ИП
МЭП
Схемы электронных вольтметров
Номенклатура вольтметров В2 — постоянного тока В3 — переменного тока В4 — импульсные В5 — фазочувствительные В6 — селективные В7 — универсальные
ВУ
УПТ
МЭП
ВУ
ИП
УПТ
МЭП
ВУ
У
ИП
МЭП
Схемы электронных вольтметров
Слайд 57

3.5.1 Амплитудный преобразователь
Преобразователь амплитудного значения. В таких преобразователях показания микроамперметра пропорциональны амплитудному значению измеряемого напряжения u(t) α = kU
В амплитудном преобразователе с открытым входом диод VD включен последовательно с высокоомным резистором и непосредственно связан с объектом измерения. Постоянные заряда и разряд связаны соотношением τз » τр
Слайд 58

3.5.1 Амплитудный преобразователь
При первой положительной полуволне измеряемого напряжения конденсатор С быстро заряжается до некоторого значения напряжения Uc1, медленно разряжаясь при отрицательной полуволне.
При второй положительной полуволне конденсатор зарядится до Uc2 > Uc1 , При значении постоянной разряда много большей периода исследуемых колебаний за 3-4 Т конденсатор зарядится до Uc ≈ Um. Показания магнитоэлектрического микроамперметра определяются средним разрядным током, пропорциональным напряжению на конденсаторе.
Слайд 59

3.5.1 Амплитудный преобразователь
Работа преобразователя с закрытым входом При положительной полуволне конденсатор С заряжается через диод VD приблизительно до Um При отрицательной полуволне диод будет заперт и конденсатор разряжается на резистор R Поскольку постоянная разряда велика, конденсатор не успевает разрядиться за период и напряжение на нем остается примерно равным Um К резистору R приложено напряжение, равное разности измеряеомго напряжения u(t) и напряжения на конденсаторе Um , т. е. ur(t) = u(t) - Um
Работа преобразователя с закрытым входом При положительной полуволне конденсатор С заряжается через диод VD приблизительно до Um При отрицательной полуволне диод будет заперт и конденсатор разряжается на резистор R Поскольку постоянная разряда велика, конденсатор не успевает разрядиться за период и напряжение на нем остается примерно равным Um К резистору R приложено напряжение, равное разности измеряеомго напряжения u(t) и напряжения на конденсаторе Um , т. е. ur(t) = u(t) - Um
Слайд 60
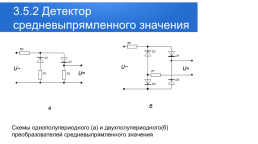
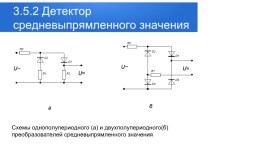
3.5.2 Детектор средневыпрямленного значения
Схемы однополупериодного (а) и двухполупериодного(б) преобразователей средневыпрямленного значения
Схемы однополупериодного (а) и двухполупериодного(б) преобразователей средневыпрямленного значения
Слайд 61

3.5.2 Детектор средневыпрямленного значения
В преобразователях средневыпрямленного значения показания α пропорциональны Ucрв. Работа мостовой схемы Ток через микроамперметр протекает в одном и том же направлении в течение обоих полупериодов переменного напряжения. При использовании линейного участка вольт-амперной характеристики диода и при открытом входе, показания микроамперметра
Графики u(t) для однополупериодного (д) и двухполупериодного(е) преобразователей средневыпрямленного значения
Слайд 62

3.5.3 Преобразователи среднеквадратического значения
В преобразователях СКВ показания α микроамперметра пропорциональны квадрату СКВ, т. е. α = kU2 Измеряемый ток пропорционален iи(t) = βu2(t) При u(t) = Umsin(ωt) , iи(t)= βUm2 (1-cos(2ωt)/2) Прибор реагирует на среднее значение, т. е. Iи=βU2
В преобразователях СКВ показания α микроамперметра пропорциональны квадрату СКВ, т. е. α = kU2 Измеряемый ток пропорционален iи(t) = βu2(t) При u(t) = Umsin(ωt) , iи(t)= βUm2 (1-cos(2ωt)/2) Прибор реагирует на среднее значение, т. е. Iи=βU2
Слайд 63

3.5.3 Преобразователи среднеквадратического значения
Напряжение смещения Ucм создает на резисторах R4 и R5 соответственно напряжения смещения Ucм1 и Ucм2. Диоды VD2 и VD3 заперты до тех пор, пока измеряемое напряжение не превысит значение напряжения смещения. При этом ток через микроамперметр будет равен сумме токов, протекающих через открытые диоды. Если напряжение u(t) > Ucм, то iи=i1+i2+i3, прибор реагирует на среднее значение тока.
Подбирая параметры цепи можно кусочно-линейно аппроксимировать ВАХ диодов и увеличить протяженность квадратичного участка.
Напряжение смещения Ucм создает на резисторах R4 и R5 соответственно напряжения смещения Ucм1 и Ucм2. Диоды VD2 и VD3 заперты до тех пор, пока измеряемое напряжение не превысит значение напряжения смещения. При этом ток через микроамперметр будет равен сумме токов, протекающих через открытые диоды. Если напряжение u(t) > Ucм, то iи=i1+i2+i3, прибор реагирует на среднее значение тока.
Подбирая параметры цепи можно кусочно-линейно аппроксимировать ВАХ диодов и увеличить протяженность квадратичного участка.
Слайд 64

3.5.3 Преобразователи среднеквадратического значения
Преобразователи среднеквадратического значения на термоэлектрических элементах используют квадратическую зависимость термоэдс от тока нагревателя
Термопреобразователь состоит из нагревателя Н и термопары Т. В схеме используются два бесконтактных термопреобразователя ТП, включенных встречно. Мощность, подводимая к ТП1 P=K1U2вх
Слайд 65

3.6 Влияние формы кривой измеряемого напряжения на показания аналоговых электронных вольтметров
Амплитудный детектор с закрытым входом реагирует только на переменное значение Uv = Umax — U0 Показания с учетом коэффицента амплитуды α = Uv / √2 Амплитудный детектор с открытым входом реагирует на амплитудное значение сигнала Показания с учетом коэффицента амплитуды α = Umax / √2 Детектор средневыпрямленного значения с открытым входом реагирует на средневыпрямленное значение сигнала Uсрв=U0=Umax tи/Т Показания с учетом коэффицента формы α = U0Кф = U0*1,11 Детектор СКВ U = Umax √tи/Т Показания α = U
Амплитудный детектор с закрытым входом реагирует только на переменное значение Uv = Umax — U0 Показания с учетом коэффицента амплитуды α = Uv / √2 Амплитудный детектор с открытым входом реагирует на амплитудное значение сигнала Показания с учетом коэффицента амплитуды α = Umax / √2 Детектор средневыпрямленного значения с открытым входом реагирует на средневыпрямленное значение сигнала Uсрв=U0=Umax tи/Т Показания с учетом коэффицента формы α = U0Кф = U0*1,11 Детектор СКВ U = Umax √tи/Т Показания α = U
Слайд 66
3.0 Классификация вольтметров
Вольтметры
Аналоговые
Цифровые
Электромеханические
Электронные
Магнитоэлектрические
Электродинамические
Электромагнитные
Электростатические
Вольтметры
Аналоговые
Цифровые
Электромеханические
Электронные
Магнитоэлектрические
Электродинамические
Электромагнитные
Электростатические
Слайд 67

3.0 Классификация вольтметров
Структурная схема аналогового электроизмерительного прибора (ЭИП)
Y
Х
Измерительная цепь
Измерительный механизм
Отсчетное устройство
α
Измерительная цепь обеспечивает преобразование измеряемой электрической величины Х в некоторую промежуточную величину Y, функционально связанную с измеряемой величиной. Измерительный механизм преобразует электромагнитную энергию в механическую, необходимую для отклонения подвижной части прибора на угол α относительно неподвижной, т. е.: α = f(Y) = F(X)
Структурная схема аналогового электроизмерительного прибора (ЭИП)
Y
Х
Измерительная цепь
Измерительный механизм
Отсчетное устройство
α
Измерительная цепь обеспечивает преобразование измеряемой электрической величины Х в некоторую промежуточную величину Y, функционально связанную с измеряемой величиной. Измерительный механизм преобразует электромагнитную энергию в механическую, необходимую для отклонения подвижной части прибора на угол α относительно неподвижной, т. е.: α = f(Y) = F(X)
Слайд 68

3.0 Классификация вольтметров
Дифференциальное уравнение моментов, описывающее работу ИМ имеет вид: На подвижную часть при ее движении действуют: Вращающий момент М Противодействующий момент Мα Момент успокоения Мусп
Дифференциальное уравнение моментов, описывающее работу ИМ имеет вид: На подвижную часть при ее движении действуют: Вращающий момент М Противодействующий момент Мα Момент успокоения Мусп
Слайд 69

3.1 Магнитоэлектрические ИМ
Принцип действия: взаимодействие магнитных полей катушки с током и магнитного потока постоянного магнита В воздушном зазоре между полюсными наконечниками магнита создается радиальное поле. Там е помещается катушка с измеряемым током. Ток пропускают через пружины, создающие противодействующий момент. Успокоение стрелки происходит за счет тормозного момента в каркасе рамки и подвесах индуцируемых токов, создающих вместе с постоянным магнитом тормозной магнитный момент. При изменении направления тока I меняется направление отклонения подвижной части ИМ. При включении ИМ в цепь переменного тока из-за инерционности подвижной части среднее значение вращающего момента за период будет равно нулю.
Принцип действия: взаимодействие магнитных полей катушки с током и магнитного потока постоянного магнита В воздушном зазоре между полюсными наконечниками магнита создается радиальное поле. Там е помещается катушка с измеряемым током. Ток пропускают через пружины, создающие противодействующий момент. Успокоение стрелки происходит за счет тормозного момента в каркасе рамки и подвесах индуцируемых токов, создающих вместе с постоянным магнитом тормозной магнитный момент. При изменении направления тока I меняется направление отклонения подвижной части ИМ. При включении ИМ в цепь переменного тока из-за инерционности подвижной части среднее значение вращающего момента за период будет равно нулю.
Слайд 70
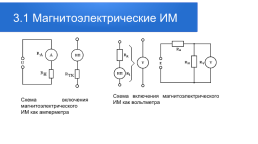
3.1 Магнитоэлектрические ИМ
Схема включения магнитоэлектрического ИМ как вольтметра
Схема включения магнитоэлектрического ИМ как амперметра
Схема включения магнитоэлектрического ИМ как вольтметра
Схема включения магнитоэлектрического ИМ как амперметра
Слайд 71
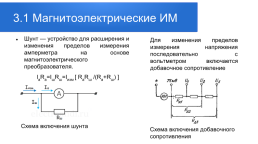
3.1 Магнитоэлектрические ИМ
Шунт — устройство для расширения и изменения пределов измерения амперметра на основе магнитоэлектрического преобразователя. IaRa=IшRш=Iизм [ RaRш /(Ra+Rш) ]
Для изменения пределов измерения напряжения последовательно с вольтметром включается добавочное сопротивление
Схема включения шунта
Схема включения добавочного сопротивления
Шунт — устройство для расширения и изменения пределов измерения амперметра на основе магнитоэлектрического преобразователя. IaRa=IшRш=Iизм [ RaRш /(Ra+Rш) ]
Для изменения пределов измерения напряжения последовательно с вольтметром включается добавочное сопротивление
Схема включения шунта
Схема включения добавочного сопротивления
Слайд 72

3.2 Электродинамические ИП
Принцип действия: взаимодействие магнитных потоков двух катушек с током. Пара катушек, соединенных последовательно, внутри которых — бескаркасная подвижная катушка на оси вращения. Для подвода тока и создания сопротивления вращению используют спиральные пружины. Энергия системы катушек: W = 0,5 I1^2L1+ 0,5 I2^2L2 +I1I2M M -взаимная индуктивность. Если потоки подвижной и неподвижной катушек совпадают то М>0,если нет, то М<0. Под действием вращающего момента подвижная катушка стремится занять такое положение, при котором направление ее МП совпадало бы с направлением МП неподвижной катушки. Она будет поворачиваться, пока вращающий и противодействующий моменты не сравняются друг с другом. Если подвижную и неподвижную катушки соединить последовательно, то итоговое отклонение будет пропорционально квадрату измеряемой электрической величины.
Принцип действия: взаимодействие магнитных потоков двух катушек с током. Пара катушек, соединенных последовательно, внутри которых — бескаркасная подвижная катушка на оси вращения. Для подвода тока и создания сопротивления вращению используют спиральные пружины. Энергия системы катушек: W = 0,5 I1^2L1+ 0,5 I2^2L2 +I1I2M M -взаимная индуктивность. Если потоки подвижной и неподвижной катушек совпадают то М>0,если нет, то М<0. Под действием вращающего момента подвижная катушка стремится занять такое положение, при котором направление ее МП совпадало бы с направлением МП неподвижной катушки. Она будет поворачиваться, пока вращающий и противодействующий моменты не сравняются друг с другом. Если подвижную и неподвижную катушки соединить последовательно, то итоговое отклонение будет пропорционально квадрату измеряемой электрической величины.
Слайд 73

3.3 Электромагнитные ИП
Принцип действия: втягивание парамегнетика в область сильного ЭМ поля. При прохождении по неподвижной плоской катушке измеряемого тока возникает магнитное поле, которое, воздействуя на лепесток 2, стремится расположить его так, чтобы энергия магнитного поля была наибольшей, т. е. втянуть лепесток внутрь катушки. Вращающий момент Шкала прибора квадратична, поэтому она в начале сжата, а в конце растянута.
Принцип действия: втягивание парамегнетика в область сильного ЭМ поля. При прохождении по неподвижной плоской катушке измеряемого тока возникает магнитное поле, которое, воздействуя на лепесток 2, стремится расположить его так, чтобы энергия магнитного поля была наибольшей, т. е. втянуть лепесток внутрь катушки. Вращающий момент Шкала прибора квадратична, поэтому она в начале сжата, а в конце растянута.
Слайд 74
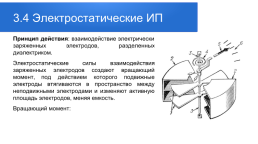
3.4 Электростатические ИП
Принцип действия: взаимодействие электрически заряженных электродов, разделенных диэлектриком. Электростатические силы взаимодействия заряженных электродов создают вращающий момент, под действием которого подвижные электроды втягиваются в пространство между неподвижными электродами и изменяют активную площадь электродов, меняя емкость. Вращающий момент:
Принцип действия: взаимодействие электрически заряженных электродов, разделенных диэлектриком. Электростатические силы взаимодействия заряженных электродов создают вращающий момент, под действием которого подвижные электроды втягиваются в пространство между неподвижными электродами и изменяют активную площадь электродов, меняя емкость. Вращающий момент:
Слайд 75
3.5 Аналоговые электронные вольтметры
Номенклатура вольтметров В2 — постоянного тока В3 — переменного тока В4 — импульсные В5 — фазочувствительные В6 — селективные В7 — универсальные
ВУ
УПТ
МЭП
ВУ
ИП
УПТ
МЭП
ВУ
У
ИП
МЭП
Схемы электронных вольтметров
Номенклатура вольтметров В2 — постоянного тока В3 — переменного тока В4 — импульсные В5 — фазочувствительные В6 — селективные В7 — универсальные
ВУ
УПТ
МЭП
ВУ
ИП
УПТ
МЭП
ВУ
У
ИП
МЭП
Схемы электронных вольтметров
Слайд 76

3.5.1 Амплитудный преобразователь
Преобразователь амплитудного значения. В таких преобразователях показания микроамперметра пропорциональны амплитудному значению измеряемого напряжения u(t) α = kU
В амплитудном преобразователе с открытым входом диод VD включен последовательно с высокоомным резистором и непосредственно связан с объектом измерения. Постоянные заряда и разряд связаны соотношением τз » τр
Слайд 77

3.5.1 Амплитудный преобразователь
При первой положительной полуволне измеряемого напряжения конденсатор С быстро заряжается до некоторого значения напряжения Uc1, медленно разряжаясь при отрицательной полуволне.
При второй положительной полуволне конденсатор зарядится до Uc2 > Uc1 , При значении постоянной разряда много большей периода исследуемых колебаний за 3-4 Т конденсатор зарядится до Uc ≈ Um. Показания магнитоэлектрического микроамперметра определяются средним разрядным током, пропорциональным напряжению на конденсаторе.
Слайд 78

3.5.1 Амплитудный преобразователь
Работа преобразователя с закрытым входом При положительной полуволне конденсатор С заряжается через диод VD приблизительно до Um При отрицательной полуволне диод будет заперт и конденсатор разряжается на резистор R Поскольку постоянная разряда велика, конденсатор не успевает разрядиться за период и напряжение на нем остается примерно равным Um К резистору R приложено напряжение, равное разности измеряеомго напряжения u(t) и напряжения на конденсаторе Um , т. е. ur(t) = u(t) - Um
Работа преобразователя с закрытым входом При положительной полуволне конденсатор С заряжается через диод VD приблизительно до Um При отрицательной полуволне диод будет заперт и конденсатор разряжается на резистор R Поскольку постоянная разряда велика, конденсатор не успевает разрядиться за период и напряжение на нем остается примерно равным Um К резистору R приложено напряжение, равное разности измеряеомго напряжения u(t) и напряжения на конденсаторе Um , т. е. ur(t) = u(t) - Um
Слайд 79
3.5.2 Детектор средневыпрямленного значения
Схемы однополупериодного (а) и двухполупериодного(б) преобразователей средневыпрямленного значения
Схемы однополупериодного (а) и двухполупериодного(б) преобразователей средневыпрямленного значения
Слайд 80

3.5.2 Детектор средневыпрямленного значения
В преобразователях средневыпрямленного значения показания α пропорциональны Ucрв. Работа мостовой схемы Ток через микроамперметр протекает в одном и том же направлении в течение обоих полупериодов переменного напряжения. При использовании линейного участка вольт-амперной характеристики диода и при открытом входе, показания микроамперметра
Графики u(t) для однополупериодного (д) и двухполупериодного(е) преобразователей средневыпрямленного значения
Слайд 81

3.5.3 Преобразователи среднеквадратического значения
В преобразователях СКВ показания α микроамперметра пропорциональны квадрату СКВ, т. е. α = kU2 Измеряемый ток пропорционален iи(t) = βu2(t) При u(t) = Umsin(ωt) , iи(t)= βUm2 (1-cos(2ωt)/2) Прибор реагирует на среднее значение, т. е. Iи=βU2
В преобразователях СКВ показания α микроамперметра пропорциональны квадрату СКВ, т. е. α = kU2 Измеряемый ток пропорционален iи(t) = βu2(t) При u(t) = Umsin(ωt) , iи(t)= βUm2 (1-cos(2ωt)/2) Прибор реагирует на среднее значение, т. е. Iи=βU2
Слайд 82

3.5.3 Преобразователи среднеквадратического значения
Напряжение смещения Ucм создает на резисторах R4 и R5 соответственно напряжения смещения Ucм1 и Ucм2. Диоды VD2 и VD3 заперты до тех пор, пока измеряемое напряжение не превысит значение напряжения смещения. При этом ток через микроамперметр будет равен сумме токов, протекающих через открытые диоды. Если напряжение u(t) > Ucм, то iи=i1+i2+i3, прибор реагирует на среднее значение тока.
Подбирая параметры цепи можно кусочно-линейно аппроксимировать ВАХ диодов и увеличить протяженность квадратичного участка.
Напряжение смещения Ucм создает на резисторах R4 и R5 соответственно напряжения смещения Ucм1 и Ucм2. Диоды VD2 и VD3 заперты до тех пор, пока измеряемое напряжение не превысит значение напряжения смещения. При этом ток через микроамперметр будет равен сумме токов, протекающих через открытые диоды. Если напряжение u(t) > Ucм, то iи=i1+i2+i3, прибор реагирует на среднее значение тока.
Подбирая параметры цепи можно кусочно-линейно аппроксимировать ВАХ диодов и увеличить протяженность квадратичного участка.
Слайд 83

3.5.3 Преобразователи среднеквадратического значения
Преобразователи среднеквадратического значения на термоэлектрических элементах используют квадратическую зависимость термоэдс от тока нагревателя
Термопреобразователь состоит из нагревателя Н и термопары Т. В схеме используются два бесконтактных термопреобразователя ТП, включенных встречно. Мощность, подводимая к ТП1 P=K1U2вх
Слайд 84

3.6 Влияние формы кривой измеряемого напряжения на показания аналоговых электронных вольтметров
Амплитудный детектор с закрытым входом реагирует только на переменное значение Uv = Umax — U0 Показания с учетом коэффицента амплитуды α = Uv / √2 Амплитудный детектор с открытым входом реагирует на амплитудное значение сигнала Показания с учетом коэффицента амплитуды α = Umax / √2 Детектор средневыпрямленного значения с открытым входом реагирует на средневыпрямленное значение сигнала Uсрв=U0=Umax tи/Т Показания с учетом коэффицента формы α = U0Кф = U0*1,11 Детектор СКВ U = Umax √tи/Т Показания α = U
Амплитудный детектор с закрытым входом реагирует только на переменное значение Uv = Umax — U0 Показания с учетом коэффицента амплитуды α = Uv / √2 Амплитудный детектор с открытым входом реагирует на амплитудное значение сигнала Показания с учетом коэффицента амплитуды α = Umax / √2 Детектор средневыпрямленного значения с открытым входом реагирует на средневыпрямленное значение сигнала Uсрв=U0=Umax tи/Т Показания с учетом коэффицента формы α = U0Кф = U0*1,11 Детектор СКВ U = Umax √tи/Т Показания α = U
Слайд 85

Метрологические основы, методы и техника измерений физических величин
Лекция №4. Средства измерений в динамическом режиме
Преподаватель: Войнов Виктор Сергеевич
Лекция №4. Средства измерений в динамическом режиме
Преподаватель: Войнов Виктор Сергеевич
Слайд 86

4.0 Средства измерений в динамическом режиме
Динамический режим — измеряемая величина меняется во времени х(t) Для того, чтобы выходной сигнал yи(t) некоторого (идеального) СИ точно отражал во в времени измеряемую величину х(t), независимо от характера ее изменения необходимо соблюдение условия: yи(t) = Kномx(t) Реальные СИ обладают динамическими(инерционными) свойствами, что приводит к более сложной зависимости между yи(t) и x(t) Наиболее полно свойства СИ могут быть описаны дифференциальными уравнениями, переходными и импульсными переходными характеристиками, частотными характеристиками и передаточными функциями.
Динамический режим — измеряемая величина меняется во времени х(t) Для того, чтобы выходной сигнал yи(t) некоторого (идеального) СИ точно отражал во в времени измеряемую величину х(t), независимо от характера ее изменения необходимо соблюдение условия: yи(t) = Kномx(t) Реальные СИ обладают динамическими(инерционными) свойствами, что приводит к более сложной зависимости между yи(t) и x(t) Наиболее полно свойства СИ могут быть описаны дифференциальными уравнениями, переходными и импульсными переходными характеристиками, частотными характеристиками и передаточными функциями.
Слайд 87

4.1 Дифференциальные уравнения
Общее уравнение динамического режима An yn(t) + An-1 yn-1(t) +...+ A1 y`(t)+ y(t) =Kномx(t) Погрешность по выходу Δy(t)=y(t)-yи(t) Погрешность по входу Δx(t) = Δy(t)/Kном Динамическая погрешность Δy(t)= -An yn(t) - An-1 yn-1(t) -...- A1 y`(t)
Определение погрешности Δy(t) по этому выражению сопряжено с трудностями, поэтому на практике используют некоторые оценки динамической погрешности, характеризующие результат изменения измеряемой величины х(t), отдельно для переходного режима и для установившегося.
Общее уравнение динамического режима An yn(t) + An-1 yn-1(t) +...+ A1 y`(t)+ y(t) =Kномx(t) Погрешность по выходу Δy(t)=y(t)-yи(t) Погрешность по входу Δx(t) = Δy(t)/Kном Динамическая погрешность Δy(t)= -An yn(t) - An-1 yn-1(t) -...- A1 y`(t)
Определение погрешности Δy(t) по этому выражению сопряжено с трудностями, поэтому на практике используют некоторые оценки динамической погрешности, характеризующие результат изменения измеряемой величины х(t), отдельно для переходного режима и для установившегося.
Слайд 88

4.1 Дифференциальные уравнения
Общее решение диф.уравнения y(t) = yc(t) + yи(t) yc(t) — общее решение, описывающее переходной процесс (затухающие свободные колебания) yи(t) — частное решение, описывающее установившийся режим (вынужденные колебания) Переходной режим оценивается временем ty Значения динамической погрешности в разных режимах могут существенно отличаться
Общее решение диф.уравнения y(t) = yc(t) + yи(t) yc(t) — общее решение, описывающее переходной процесс (затухающие свободные колебания) yи(t) — частное решение, описывающее установившийся режим (вынужденные колебания) Переходной режим оценивается временем ty Значения динамической погрешности в разных режимах могут существенно отличаться
Слайд 89

4.1 Дифференциальные уравнения
Порядок диф. уравнения определяется динамическими свойствами СИ и в общем случае может быть высоким. Дифференциальные уравнения высокого порядка могут быть представлены системой дифференциальных уравнений более низкого порядка. Это эквивалентно замене сложного в динамическом отношении устройства на совокупность более простых. Такие простые в динамическом отношении устройства называются звеньями
Порядок диф. уравнения определяется динамическими свойствами СИ и в общем случае может быть высоким. Дифференциальные уравнения высокого порядка могут быть представлены системой дифференциальных уравнений более низкого порядка. Это эквивалентно замене сложного в динамическом отношении устройства на совокупность более простых. Такие простые в динамическом отношении устройства называются звеньями
Слайд 90

4.1 Дифференциальные уравнения
Характеристики звена 1-го порядка T1 y`(t)+ y(t) =Kномx(t), где Т1 — постоянная времени звена первого порядка. Динамическая погрешность по входу Δx(t) = -T1 y`(t)/Kном Оценка максимума модуля погрешности: max y`(t) ≤ ωmym ≤ ωmxmkm km=kном => max Δx(t) ≤ ωmxmT1 Оценка максимальной приведенной погрешности max γ = max Δx(t)/xN ≤ωmT1 /2 = ωm / 2ω0
Характеристики звена 1-го порядка T1 y`(t)+ y(t) =Kномx(t), где Т1 — постоянная времени звена первого порядка. Динамическая погрешность по входу Δx(t) = -T1 y`(t)/Kном Оценка максимума модуля погрешности: max y`(t) ≤ ωmym ≤ ωmxmkm km=kном => max Δx(t) ≤ ωmxmT1 Оценка максимальной приведенной погрешности max γ = max Δx(t)/xN ≤ωmT1 /2 = ωm / 2ω0
Слайд 91

4.1 Дифференциальные уравнения
Динамическое звено 2-го порядка A2 y“(t) + A1 y`(t) + y(t) = Kномx(t) или 1/ω20 y“(t) + 2β/ω0 y`(t) + y(t) = Kномx(t) Ω0 — частота собственных колебаний звена, β — коэффициент демпфирования Оценка динамической погрешности по входу для звена 2-го порядка
Динамическое звено 2-го порядка A2 y“(t) + A1 y`(t) + y(t) = Kномx(t) или 1/ω20 y“(t) + 2β/ω0 y`(t) + y(t) = Kномx(t) Ω0 — частота собственных колебаний звена, β — коэффициент демпфирования Оценка динамической погрешности по входу для звена 2-го порядка
Слайд 92

4.2 Переходные характеристики
Переходная характеристика h(t) - это реакция системы на входное воздействие — скачок 1(t) Импульсная переходная характеристика g(t) - это реакция системы на входное воздействие в виде дельта-функции Поскольку d1(t)/dt = δ(t), то dh(t)/dt = g(t) Как и диф.уравнение, эти характеристики в полной мере определяют динамические свойства СИ
Переходная характеристика h(t) - это реакция системы на входное воздействие — скачок 1(t) Импульсная переходная характеристика g(t) - это реакция системы на входное воздействие в виде дельта-функции Поскольку d1(t)/dt = δ(t), то dh(t)/dt = g(t) Как и диф.уравнение, эти характеристики в полной мере определяют динамические свойства СИ
Слайд 93

4.2 Переходные характеристики
Характеристики звена 1-го порядка Переходная h(t) = kном(1-exp(-t/T1)) Импульсная переходная g(t) = kном/T1exp(-t/T1) Время установления tу tу = T1 ln(h(∞)/Δh)
Характеристики звена 1-го порядка Переходная h(t) = kном(1-exp(-t/T1)) Импульсная переходная g(t) = kном/T1exp(-t/T1) Время установления tу tу = T1 ln(h(∞)/Δh)
Слайд 94

4.2 Переходные характеристики
Для звена 2-го порядка вид характеристик h(t) и g(t) зависит от коэффициента демпфирования β. Рассматриваются три режима 1)Колебательный (β<1) 2)Критический (β=1) 3)Апериодический (β>1)
Для звена 2-го порядка вид характеристик h(t) и g(t) зависит от коэффициента демпфирования β. Рассматриваются три режима 1)Колебательный (β<1) 2)Критический (β=1) 3)Апериодический (β>1)
Слайд 95

4.2 Переходные характеристики
При колебательном характере переходного процесса в ряде случаев оценивают первое максимальное отклонение Δh выходного сигнала от установившегося значения h(∞). Для этого определяют значение первого экстремума переходной характеристики t1Э из g(t1Э)=0
При колебательном характере переходного процесса в ряде случаев оценивают первое максимальное отклонение Δh выходного сигнала от установившегося значения h(∞). Для этого определяют значение первого экстремума переходной характеристики t1Э из g(t1Э)=0
Слайд 96

4.3 Частотные характеристики
Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через СИ. Различают несколько частотных характеристик СИ: Амплитудно-фазовая характеристика Комплексная частотная характеристика Амплитудно-частотная характеристика (АЧХ) Фазочастотная характеристика (ФЧХ)
Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через СИ. Различают несколько частотных характеристик СИ: Амплитудно-фазовая характеристика Комплексная частотная характеристика Амплитудно-частотная характеристика (АЧХ) Фазочастотная характеристика (ФЧХ)
Слайд 97

4.3 Частотные характеристики
Амплитудно-фазовая характеристика. Метрологическая характеристика средства измерений, представляющая собой зависящее от круговой частоты отношение преобразования Фурье выходного сигнала линейного средства измерений к преобразованию Фурье его входного сигнала при нулевых начальных условиях. Математическая формулировка: амплитудно-фазовая характеристика K(jω) = Y(jω)/X(jω), Y(jω) - преобразование Фурье отклика y(t) средства измерений на испытательный х(t) сигнал; X(jω) преобразование Фурье сигнала x(t).
Амплитудно-фазовая характеристика. Метрологическая характеристика средства измерений, представляющая собой зависящее от круговой частоты отношение преобразования Фурье выходного сигнала линейного средства измерений к преобразованию Фурье его входного сигнала при нулевых начальных условиях. Математическая формулировка: амплитудно-фазовая характеристика K(jω) = Y(jω)/X(jω), Y(jω) - преобразование Фурье отклика y(t) средства измерений на испытательный х(t) сигнал; X(jω) преобразование Фурье сигнала x(t).
Слайд 98

4.3 Частотные характеристики
Комплексная частотная характеристика Динамическая характеристика средства измерений, представляющая собой его амплитудно-фазовую характеристику, отнесенную к статическому коэффициенту преобразования средства измерений. 1. Математическая формулировка: приведенная комплексная частотная характеристика где K(jω) - амплитудно-фазовая характеристика средства измерений со статическим коэффициентом преобразования K 2. Комплексная частотная характеристика используется, главным образом, для описания линейного средства измерений и представляет собой его полную динамическую характеристику. 3. Комплексная частотная характеристика линейного средства измерений представляет собой преобразование Фурье его приведенной импульсной характеристики 4. Комплексная частотная характеристика может быть использована для описания нелинейного средства измерений. В этом случае она определяется с использованием соответствующего испытательному сигналу статического коэффициента преобразования нелинейного средства измерений. 5. Комплексная частотная характеристика нелинейного средства измерений представляет собой его частную динамическую характеристику. 6. Нелинейное средство измерений характеризуют совокупностью комплексных частотных характеристик, соответствующих различным испытательным сигналам
Комплексная частотная характеристика Динамическая характеристика средства измерений, представляющая собой его амплитудно-фазовую характеристику, отнесенную к статическому коэффициенту преобразования средства измерений. 1. Математическая формулировка: приведенная комплексная частотная характеристика где K(jω) - амплитудно-фазовая характеристика средства измерений со статическим коэффициентом преобразования K 2. Комплексная частотная характеристика используется, главным образом, для описания линейного средства измерений и представляет собой его полную динамическую характеристику. 3. Комплексная частотная характеристика линейного средства измерений представляет собой преобразование Фурье его приведенной импульсной характеристики 4. Комплексная частотная характеристика может быть использована для описания нелинейного средства измерений. В этом случае она определяется с использованием соответствующего испытательному сигналу статического коэффициента преобразования нелинейного средства измерений. 5. Комплексная частотная характеристика нелинейного средства измерений представляет собой его частную динамическую характеристику. 6. Нелинейное средство измерений характеризуют совокупностью комплексных частотных характеристик, соответствующих различным испытательным сигналам
Слайд 99

4.3 Частотные характеристики
Амплитудно-частотная характеристика (АЧХ) K(ω) Частная динамическая характеристика средства измерений, представляющая собой зависимость от частоты гармонических испытательных сигналов амплитуды установившихся откликов на указанные сигналы (для линейных средств измерений), либо амплитуды первой гармоники установившихся откликов на указанные сигналы (для нелинейных средств измерений), отнесенной к амплитуде испытательных сигналов и статическому коэффициенту преобразования. 1. Математическая формулировка: для линейных средств измерений где b(ω) - амплитуда отклика y(t) = b(ω)sin[ωt +ψ(ω)]; на испытательный сигнал x(t) = a(ω)sin[ωt + φ(ω)]; для нелинейных средств измерений где B1(ω) - амплитуда первой гармоники отклика на испытательный сигнал х(t). 2. Амплитудно-частотная характеристика средства измерений представляет собой модуль его комплексной частотной характеристики: K(ω) = mod W(jω). 3. Амплитудно-частотная характеристика минимально-фазового линейного средства измерений однозначно связана с его фазочастотной характеристикой.
Амплитудно-частотная характеристика (АЧХ) K(ω) Частная динамическая характеристика средства измерений, представляющая собой зависимость от частоты гармонических испытательных сигналов амплитуды установившихся откликов на указанные сигналы (для линейных средств измерений), либо амплитуды первой гармоники установившихся откликов на указанные сигналы (для нелинейных средств измерений), отнесенной к амплитуде испытательных сигналов и статическому коэффициенту преобразования. 1. Математическая формулировка: для линейных средств измерений где b(ω) - амплитуда отклика y(t) = b(ω)sin[ωt +ψ(ω)]; на испытательный сигнал x(t) = a(ω)sin[ωt + φ(ω)]; для нелинейных средств измерений где B1(ω) - амплитуда первой гармоники отклика на испытательный сигнал х(t). 2. Амплитудно-частотная характеристика средства измерений представляет собой модуль его комплексной частотной характеристики: K(ω) = mod W(jω). 3. Амплитудно-частотная характеристика минимально-фазового линейного средства измерений однозначно связана с его фазочастотной характеристикой.
Слайд 100

4.3 Частотные характеристики
Фазочастотная характеристика (ФЧХ) φ(ω) Частная динамическая характеристика средства измерений, представляющая собой зависящую от частоты гармонического испытательного сигнала разность фаз между установившимся откликом средства измерений и указанным сигналом (для линейного средства измерений), либо разность фаз между первой гармоникой установившегося отклика и указанным сигналом (для нелинейного средства измерений). Математическая формулировка: для линейного средства измерений где ψ(ω) - начальная фаза отклика y(t) = b(ω)sin[ωt +ψ(ω)]; на испытательный сигнал x(t) = a(ω)sin[ωt + φ(ω)]; для нелинейного средства измерений Фнелин(ω) = ψ1(ω) — φ(ω), где ψ1(ω) - начальная фаза первой гармоники отклика на испытательный сигнал x(t) = a(ω)sin[ωt + φ(ω)].
Фазочастотная характеристика (ФЧХ) φ(ω) Частная динамическая характеристика средства измерений, представляющая собой зависящую от частоты гармонического испытательного сигнала разность фаз между установившимся откликом средства измерений и указанным сигналом (для линейного средства измерений), либо разность фаз между первой гармоникой установившегося отклика и указанным сигналом (для нелинейного средства измерений). Математическая формулировка: для линейного средства измерений где ψ(ω) - начальная фаза отклика y(t) = b(ω)sin[ωt +ψ(ω)]; на испытательный сигнал x(t) = a(ω)sin[ωt + φ(ω)]; для нелинейного средства измерений Фнелин(ω) = ψ1(ω) — φ(ω), где ψ1(ω) - начальная фаза первой гармоники отклика на испытательный сигнал x(t) = a(ω)sin[ωt + φ(ω)].
Слайд 101

4.3 Частотные характеристики
Слайд 102

4.3 Частотные характеристики
Рассмотрим возможность оценки динамических погрешностей по известным АЧХ и ФЧХ Для частот ниже частоты среза K(ω)=kном,φ(ω) =-tзω Динамическая погрешность δi=[K(ωi) — kном]/kном Фазовый сдвиг ωt = φ/2 max Δy(t) = 2kном Xm sinφ/2
Рассмотрим возможность оценки динамических погрешностей по известным АЧХ и ФЧХ Для частот ниже частоты среза K(ω)=kном,φ(ω) =-tзω Динамическая погрешность δi=[K(ωi) — kном]/kном Фазовый сдвиг ωt = φ/2 max Δy(t) = 2kном Xm sinφ/2
Слайд 103

4.4 Передаточные функции
Преобразование Лапласа Функции времени f(t) ставится в соответствие образ F(p) Зависимость выходного сигнала от входного после преобразования примет вид Anpn + An-1pn-1 + … + A1p + Y(p) = kном X(p) Передаточная функция K(p) = Y(p) / X(p) Передаточную функцию можно представить в виде K(p) = ∏ki/(p-pi) что можно интерпретировать, как представление сложного передаточного звена в виде последовательности более простых звеньев.
Передаточные функции некоторых простых звеньев
Преобразование Лапласа Функции времени f(t) ставится в соответствие образ F(p) Зависимость выходного сигнала от входного после преобразования примет вид Anpn + An-1pn-1 + … + A1p + Y(p) = kном X(p) Передаточная функция K(p) = Y(p) / X(p) Передаточную функцию можно представить в виде K(p) = ∏ki/(p-pi) что можно интерпретировать, как представление сложного передаточного звена в виде последовательности более простых звеньев.
Передаточные функции некоторых простых звеньев
Слайд 104

4.5 Взаимосвязь динамических характеристик СИ
Слайд 105

Метрологические основы, методы и техника измерений физических величин
Лекция №5: Измерительные генераторы, осциллографы и частотомеры
Преподаватель: Войнов Виктор Сергеевич
Лекция №5: Измерительные генераторы, осциллографы и частотомеры
Преподаватель: Войнов Виктор Сергеевич
Слайд 106

5.1 Измерительные генераторы
Измерительные генераторы(ИГ) — источники, вырабатывающие стабильные сигналы с известными параметрами, мощностью и формой. ИГ классифицируются: По диапазону частот По форме генерируемых сигналов По виду модуляции
Измерительные генераторы(ИГ) — источники, вырабатывающие стабильные сигналы с известными параметрами, мощностью и формой. ИГ классифицируются: По диапазону частот По форме генерируемых сигналов По виду модуляции
Слайд 107

5.1 Измерительные генераторы
По диапазону частот.По форме сигналов.По виду модуляции
Инфранизкочастотные До 20 Гц.Г3 — синусоидальный сигнал низкой частоты.Амплитудная синусоидальная
Низкочастотные 20 Гц -200 кГц.Г4 — синусоидальный сигнал высокой частоты.Частотная синусоидальная
Высокочастотные 200 кГц — 50 МГц.Г5 — периодических импульсов прямоугольной формы.Импульсная
Сверхвысокочастотные с коаксиальным выходом 50 МГц-10 ГГц.Г6 — сигналов специальной формы.Частотная
Сверхвысокочастотные с коаксиальным выходом больше 10 ГГц.Г8 — качающейся частоты.Фазовая
.Г2 — шумовых сигналов.Комбинированная
По диапазону частот.По форме сигналов.По виду модуляции
Инфранизкочастотные До 20 Гц.Г3 — синусоидальный сигнал низкой частоты.Амплитудная синусоидальная
Низкочастотные 20 Гц -200 кГц.Г4 — синусоидальный сигнал высокой частоты.Частотная синусоидальная
Высокочастотные 200 кГц — 50 МГц.Г5 — периодических импульсов прямоугольной формы.Импульсная
Сверхвысокочастотные с коаксиальным выходом 50 МГц-10 ГГц.Г6 — сигналов специальной формы.Частотная
Сверхвысокочастотные с коаксиальным выходом больше 10 ГГц.Г8 — качающейся частоты.Фазовая
.Г2 — шумовых сигналов.Комбинированная
Слайд 108

5.1.1 Низкочастотные ИГ
Метрологические характеристики Коэффициент нелинейных искажений — отношение среднеквадратического значения суммы амплитуд всех гармоник сигнала, кроме первой, к амплитуде первой гармоники сигнала Коэффициент перекрытия- отношение максимальной генерируемой частоты к минимальной Kпер = fmax / fmin Стабильность частоты (f1 — f0)/f0 = Δf/f0 Абсолютная погрешность установки частоты Δf = ±(δif + n)
Метрологические характеристики Коэффициент нелинейных искажений — отношение среднеквадратического значения суммы амплитуд всех гармоник сигнала, кроме первой, к амплитуде первой гармоники сигнала Коэффициент перекрытия- отношение максимальной генерируемой частоты к минимальной Kпер = fmax / fmin Стабильность частоты (f1 — f0)/f0 = Δf/f0 Абсолютная погрешность установки частоты Δf = ±(δif + n)
Слайд 109
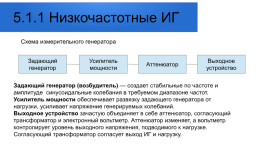
5.1.1 Низкочастотные ИГ
Схема измерительного генератора
Задающий генератор
Усилитель мощности
Аттенюатор
Выходное устройство
Задающий генератор (возбудитель) — создает стабильные по частоте и амплитуде синусоидальные колебания в требуемом диапазоне частот. Усилитель мощности обеспечивает развязку задающего генератора от нагрузки, усиливает напряжение генерируемых колебаний. Выходное устройство зачастую объединяет в себе аттенюатор, согласующий трансформатор и электронный вольтметр. Аттенюатор изменяет, а вольтметр контролирует уровень выходного напряжения, подводимого к нагрузке. Согласующий трансформатор согласует выход ИГ и нагрузку.
Схема измерительного генератора
Задающий генератор
Усилитель мощности
Аттенюатор
Выходное устройство
Задающий генератор (возбудитель) — создает стабильные по частоте и амплитуде синусоидальные колебания в требуемом диапазоне частот. Усилитель мощности обеспечивает развязку задающего генератора от нагрузки, усиливает напряжение генерируемых колебаний. Выходное устройство зачастую объединяет в себе аттенюатор, согласующий трансформатор и электронный вольтметр. Аттенюатор изменяет, а вольтметр контролирует уровень выходного напряжения, подводимого к нагрузке. Согласующий трансформатор согласует выход ИГ и нагрузку.
Слайд 110
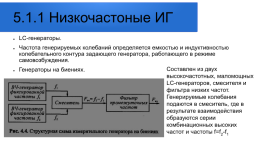
5.1.1 Низкочастоные ИГ
LC-генераторы. Частота генерируемых колебаний определяется емкостью и индуктивностью колебательного контура задающего генератора, работающего в режиме самовозбуждения. Генераторы на биениях.
Составлен из двух высокочастотных, маломощных LC-генераторов, смесителя и фильтра низких частот. Генерируемые колебания подаются в смеситель, где в результате взаимодействия образуются серии комбинационных высоких частот и частоты f=f2-f1
LC-генераторы. Частота генерируемых колебаний определяется емкостью и индуктивностью колебательного контура задающего генератора, работающего в режиме самовозбуждения. Генераторы на биениях.
Составлен из двух высокочастотных, маломощных LC-генераторов, смесителя и фильтра низких частот. Генерируемые колебания подаются в смеситель, где в результате взаимодействия образуются серии комбинационных высоких частот и частоты f=f2-f1
Слайд 111

5.1.1 Низкочастоные ИГ
RC- генератор Двухкаскадный усилитель с положительной обратной связью. Обратная связь создается фазирующим делителем, образованная элементами R1 R2 C1 C2, предназначенными для генерации на одной частоте. Условие генерации: Kβexp(iφ+iψ)=1 Поскольку β= Z2 /(Z1 +Z2), а R1 R2 =R, и C1 C2 =C, то β=1/[3 + i(ωCR-1/ωCR)], следовательно К=3 Генератор с малым К работает нестабильно, поэтому обычно вводится дополнительная цепь обратной связи, которая уменьшает коэффициент до 3.
RC- генератор Двухкаскадный усилитель с положительной обратной связью. Обратная связь создается фазирующим делителем, образованная элементами R1 R2 C1 C2, предназначенными для генерации на одной частоте. Условие генерации: Kβexp(iφ+iψ)=1 Поскольку β= Z2 /(Z1 +Z2), а R1 R2 =R, и C1 C2 =C, то β=1/[3 + i(ωCR-1/ωCR)], следовательно К=3 Генератор с малым К работает нестабильно, поэтому обычно вводится дополнительная цепь обратной связи, которая уменьшает коэффициент до 3.
Слайд 112

5.1.2 Низкочастотные цифровые генераторы
В цифровых генераторах реализуется метод цифроаналогового преобразования для формирования квазисинусоидальной кривой. Сигнал аппроксимируется с известной степенью точности кусочно-ступенчатым сигналом: С равномерным расположением узлов аппроксимации по времени С равноотстоящими узлами аппроксимации по уровню С оптимальным(неравномерным) выбором узлов аппроксимации по времени и уровню
В цифровых генераторах реализуется метод цифроаналогового преобразования для формирования квазисинусоидальной кривой. Сигнал аппроксимируется с известной степенью точности кусочно-ступенчатым сигналом: С равномерным расположением узлов аппроксимации по времени С равноотстоящими узлами аппроксимации по уровню С оптимальным(неравномерным) выбором узлов аппроксимации по времени и уровню
Слайд 113
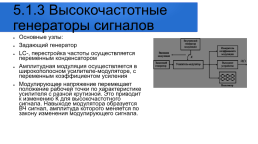
5.1.3 Высокочастотные генераторы сигналов
Основные узлы: Задающий генератор LC-, перестройка частоты осуществляется переменным конденсатором Амплитудная модуляция осуществляется в широкополосном усилителе-модуляторе, с переменным коэффициентом усиления Модулирующее напряжение перемещает положение рабочей точки по характеристике усилителя с разной крутизной. Это приводит к изменению К для высокочастотного сигнала. Навыходе модулятора образуется ВЧ сигнал, амплитуда которого меняется по закону изменения модулирующего сигнала.
Основные узлы: Задающий генератор LC-, перестройка частоты осуществляется переменным конденсатором Амплитудная модуляция осуществляется в широкополосном усилителе-модуляторе, с переменным коэффициентом усиления Модулирующее напряжение перемещает положение рабочей точки по характеристике усилителя с разной крутизной. Это приводит к изменению К для высокочастотного сигнала. Навыходе модулятора образуется ВЧ сигнал, амплитуда которого меняется по закону изменения модулирующего сигнала.
Слайд 114

5.2 Электронно-лучевые осциллографы
Осциллограф — прибор, предназначенный для наблюдения формы и измерения амплитудных и временных параметров электрически сигналов в диапазоне частот от постоянного тока до десятков ГГц Электронно-лучевой осциллограф (ЭЛО) -устройство, основным элементом которого является электронно0лучевая трубка с электростатическим управлением луча и люминесцирующим экраном. Для преобразования исследуемого сигнала луч перемещается в двух взаимоперпендикулярных направлениях
Осциллограф — прибор, предназначенный для наблюдения формы и измерения амплитудных и временных параметров электрически сигналов в диапазоне частот от постоянного тока до десятков ГГц Электронно-лучевой осциллограф (ЭЛО) -устройство, основным элементом которого является электронно0лучевая трубка с электростатическим управлением луча и люминесцирующим экраном. Для преобразования исследуемого сигнала луч перемещается в двух взаимоперпендикулярных направлениях
Слайд 115
5.2.1Схема электронно-лучевого одноканального осциллографа
На канал вертикального отклонения (ВО) подается исследуемый сигнал. Канал горизонтального отклонения (ГО) служит для формирования развертки. Схемы синхронизации и запуска синхронизируют импульсы развертки и исследуемого сигнала.
На канал вертикального отклонения (ВО) подается исследуемый сигнал. Канал горизонтального отклонения (ГО) служит для формирования развертки. Схемы синхронизации и запуска синхронизируют импульсы развертки и исследуемого сигнала.
Слайд 116

5.2.1Схема электронно-лучевого одноканального осциллографа
Коэффициент отклонения Ко (В/дел) — отношение напряжения входного сигнала u к отклонению луча на экране h Ко = u/h Коэффициент развертки Кр (Время/дел) показывает время, за которое электронный луч проходит одно деление по горизонтали Кр =Тр / lр
Коэффициент отклонения Ко (В/дел) — отношение напряжения входного сигнала u к отклонению луча на экране h Ко = u/h Коэффициент развертки Кр (Время/дел) показывает время, за которое электронный луч проходит одно деление по горизонтали Кр =Тр / lр
Слайд 117

5.2.1Схема электронно-лучевого одноканального осциллографа
Принцип работы осциллографа: Исследуемый сигнал (вход Y) подается на канал ВО Прошедший через аттенюатор и предварительный усилитель сигнал задерживается линией задержки на время, необходимое для срабатывания канала ГО осциллографа Выходной усилитель ВО преобразует сигнал в симметричный, усиливает сигнал до значения, удобного для наблюдения Устойчивость изображения достигается синхронизацией сигнала развертки с исследуемым сигналом Схема синхронизации запускается как от внутреннего, так и от внешнего сигналов. При внутренней снимается часть сигнала по мощности. Генератор развертки запускается по синхроимпульсу. Вырабатывает пилообразное напряжение, у которого время прямого хода значительно выше времени обратного Положительно нарастающее пилообразное напряжение подается на правую пластину, а отрицательное — на левую. В результате луч по экрану трубки проходит слева направо за определенное время.
Принцип работы осциллографа: Исследуемый сигнал (вход Y) подается на канал ВО Прошедший через аттенюатор и предварительный усилитель сигнал задерживается линией задержки на время, необходимое для срабатывания канала ГО осциллографа Выходной усилитель ВО преобразует сигнал в симметричный, усиливает сигнал до значения, удобного для наблюдения Устойчивость изображения достигается синхронизацией сигнала развертки с исследуемым сигналом Схема синхронизации запускается как от внутреннего, так и от внешнего сигналов. При внутренней снимается часть сигнала по мощности. Генератор развертки запускается по синхроимпульсу. Вырабатывает пилообразное напряжение, у которого время прямого хода значительно выше времени обратного Положительно нарастающее пилообразное напряжение подается на правую пластину, а отрицательное — на левую. В результате луч по экрану трубки проходит слева направо за определенное время.
Слайд 118
5.2.2 Основные узлы ЭЛО
Электронно-лучевая трубка
Электроны, вышедшие из материала катода в результате термоэлектронной эмиссии, формируют пучок, ускоряемый приложенным в трубке напряжением. Электронный пучок проходит через ряд фокусирующих и управляющих электродов и отклоняется трактами ВО и ГО для формирования устойчивой картины сигнала на экране, покрытым люминофором.
Электронно-лучевая трубка
Электроны, вышедшие из материала катода в результате термоэлектронной эмиссии, формируют пучок, ускоряемый приложенным в трубке напряжением. Электронный пучок проходит через ряд фокусирующих и управляющих электродов и отклоняется трактами ВО и ГО для формирования устойчивой картины сигнала на экране, покрытым люминофором.
Слайд 119

5.2.2 Основные узлы ЭЛО
Канал вертикального отклонения. Предназначен для усиления/ослабления исследуемых электрических сигналов до требуемого значения. Состоит из входного устройства и усилителя с линией задержки. Входное устройство позволяет расширить пределы измеряемых входных напряжений и обеспечить необходимое входное сопротивление. С помощью аттенюатора регулируется Ко на всей полосе частот Усилитель ВО для преобразования измеряемого сигнала в два противофазных сигнала и усиления их до значения, достаточного для отклонения луча по вертикали Линия задержки представляет собой однопроводной коаксиальный кабель или искусственные длинные линии Канал ВО определяет АЧХ осциллографа и полосу пропускания
АЧХ осциллографа. Ослабление в 3 дБ или Ко =0,707K достигается на частоте среза fгр
Канал вертикального отклонения. Предназначен для усиления/ослабления исследуемых электрических сигналов до требуемого значения. Состоит из входного устройства и усилителя с линией задержки. Входное устройство позволяет расширить пределы измеряемых входных напряжений и обеспечить необходимое входное сопротивление. С помощью аттенюатора регулируется Ко на всей полосе частот Усилитель ВО для преобразования измеряемого сигнала в два противофазных сигнала и усиления их до значения, достаточного для отклонения луча по вертикали Линия задержки представляет собой однопроводной коаксиальный кабель или искусственные длинные линии Канал ВО определяет АЧХ осциллографа и полосу пропускания
АЧХ осциллографа. Ослабление в 3 дБ или Ко =0,707K достигается на частоте среза fгр
Слайд 120

5.2.2 Основные узлы ЭЛО
Канал ГО В канале ГО формируется линейно изменяющееся напряжение, синхронное с исследуемым сигналом, амплитуда которого достаточна для отклонения луча ЭЛТ на весь экран по горизонтали При изменении длительности развертки изменяется скорость движения луча → масштаб времени Фиксированному Up соответствует горизонтальное отклонение lp Нелинейность развертки — изменение Кр в пределах рабочей части экрана относительно его фактического значения в центральной части. Скорость развертки Vp = 1/Kp = lp / Tp
Канал ГО В канале ГО формируется линейно изменяющееся напряжение, синхронное с исследуемым сигналом, амплитуда которого достаточна для отклонения луча ЭЛТ на весь экран по горизонтали При изменении длительности развертки изменяется скорость движения луча → масштаб времени Фиксированному Up соответствует горизонтальное отклонение lp Нелинейность развертки — изменение Кр в пределах рабочей части экрана относительно его фактического значения в центральной части. Скорость развертки Vp = 1/Kp = lp / Tp
Слайд 121

5.2.2 Основные узлы ЭЛО
Канал ГО Синхронизация — процесс, при котором развертка становится зависимой от исследуемого сигнала для получения неподвижного изображения. Внутренняя синхронизация — процесс, при котором сигнал,управляющий запуском ГР, подается из внутренней цепи ЭО, на которую воздействует исследуемый сигнал Внешняя синхронизация — процесс, при котором управляющий сигнал подается извне.
Временные диаграммы напряжений при исследовании сигнала с автоколебательной разверткой
Канал ГО Синхронизация — процесс, при котором развертка становится зависимой от исследуемого сигнала для получения неподвижного изображения. Внутренняя синхронизация — процесс, при котором сигнал,управляющий запуском ГР, подается из внутренней цепи ЭО, на которую воздействует исследуемый сигнал Внешняя синхронизация — процесс, при котором управляющий сигнал подается извне.
Временные диаграммы напряжений при исследовании сигнала с автоколебательной разверткой
Слайд 122
5.2.2 Основные узлы ЭЛО
Выходной усилитель ГО предназначен для преобразования пилообразного напряжения ГР в два противофазных сигнала и для усиления их до значений, достаточных для отклонения луча по горизонтали. В ряде осциллографов предусмотрена схема с изменяющимся скачкообразно Кус усилителя, что позволяет увеличивать напряжение развертки. Кр“= KpMp, где Mp -множитель растяжки.
Растяжение изображения при использовании скачкообразно меняющегося Кр
Выходной усилитель ГО предназначен для преобразования пилообразного напряжения ГР в два противофазных сигнала и для усиления их до значений, достаточных для отклонения луча по горизонтали. В ряде осциллографов предусмотрена схема с изменяющимся скачкообразно Кус усилителя, что позволяет увеличивать напряжение развертки. Кр“= KpMp, где Mp -множитель растяжки.
Растяжение изображения при использовании скачкообразно меняющегося Кр
Слайд 123

5.2.3 Параметры ЭЛО
Время нарастания переходной характеристики Tн =0,35/ fв Если требуется без искажений воспроизвести фронт прямоугольного импульса, то необходимо выполнить условие fв >0,35/tф Погрешности работы осциллографа: Погрешность номинального Ко Погрешность преобразования, вызванной неравномерностью переходной характеристики Визуальной погрешности отсчета геометрических размеров сигнала
Переходная характеристика ЭЛО
Время нарастания переходной характеристики Tн =0,35/ fв Если требуется без искажений воспроизвести фронт прямоугольного импульса, то необходимо выполнить условие fв >0,35/tф Погрешности работы осциллографа: Погрешность номинального Ко Погрешность преобразования, вызванной неравномерностью переходной характеристики Визуальной погрешности отсчета геометрических размеров сигнала
Переходная характеристика ЭЛО
Слайд 124
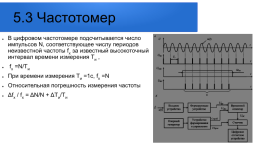
5.3 Частотомер
В цифровом частотомере подсчитывается число импульсов N, соответствующее числу периодов неизвестной частоты fx за известный высокоточный интервал времени измерения Ти , fx =N/Ти При времени измерения Ти =1с, fx =N Относительная погрешность измерения частоты Δfx / fx = ΔN/N + ΔТи/Ти
В цифровом частотомере подсчитывается число импульсов N, соответствующее числу периодов неизвестной частоты fx за известный высокоточный интервал времени измерения Ти , fx =N/Ти При времени измерения Ти =1с, fx =N Относительная погрешность измерения частоты Δfx / fx = ΔN/N + ΔТи/Ти
Слайд 125

Метрологические основы, методы и техника измерений физических величин
Лекция №6 Измерение параметров цепей с сосредоточенными постоянными
Преподаватель: Войнов Виктор Сергеевич
Лекция №6 Измерение параметров цепей с сосредоточенными постоянными
Преподаватель: Войнов Виктор Сергеевич
Слайд 126

6.0 Общие сведения
Параметры цепей с сосредоточенными постоянными: Сопротивление R Емкость С Тангенс угла потерь конденсатора Индуктивность L Добротность Q Взаимоиндуктивность Полное сопротивление цепи Z Измерение параметров цепи может быть прямое и косвенное. Прямые измерения выполняются методами непосредственной оценки, косвенные — методами сравнения.
Параметры цепей с сосредоточенными постоянными: Сопротивление R Емкость С Тангенс угла потерь конденсатора Индуктивность L Добротность Q Взаимоиндуктивность Полное сопротивление цепи Z Измерение параметров цепи может быть прямое и косвенное. Прямые измерения выполняются методами непосредственной оценки, косвенные — методами сравнения.
Слайд 127

6.0 Общие сведения
Значения сопротивления, емкости и индуктивности отдельных элементов определяются по номинальному ряду, ограничивающему погрешность значения соответствующего параметра. Ряд значений получается разбивкой интервала от 1 до 10 на соответствующее число значений, т. е. ряд Е24 имеет 24 базовых значения. Прочие получаются путем умножения 10 в произвольной степени на номинальное значение ряда.
Значения сопротивления, емкости и индуктивности отдельных элементов определяются по номинальному ряду, ограничивающему погрешность значения соответствующего параметра. Ряд значений получается разбивкой интервала от 1 до 10 на соответствующее число значений, т. е. ряд Е24 имеет 24 базовых значения. Прочие получаются путем умножения 10 в произвольной степени на номинальное значение ряда.
Слайд 128
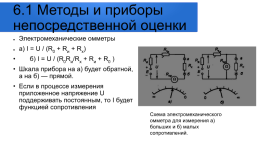
6.1 Методы и приборы непосредственной оценки
Электромеханические омметры а) I = U / (R0 + Rи + Rх) б) I = U / (R0Rи/Rх + Rи + R0 ) Шкала прибора на а) будет обратной, а на б) — прямой. Если в процессе измерения приложенное напряжение U поддерживать постоянным, то I будет функцией сопротивления
Схема электромеханического омметра для измерения а) больших и б) малых сопротивлений.
Электромеханические омметры а) I = U / (R0 + Rи + Rх) б) I = U / (R0Rи/Rх + Rи + R0 ) Шкала прибора на а) будет обратной, а на б) — прямой. Если в процессе измерения приложенное напряжение U поддерживать постоянным, то I будет функцией сопротивления
Схема электромеханического омметра для измерения а) больших и б) малых сопротивлений.
Слайд 129
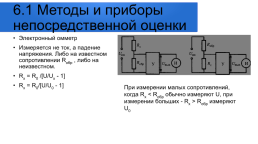
6.1 Методы и приборы непосредственной оценки
Электронный омметр Измеряется не ток, а падение напряжения. Либо на известном сопротивлении Rобр , либо на неизвестном. Rx = R0 /[U/Ux - 1] Rx = R0/[U/U0 - 1]
При измерении малых сопротивлений, когда Rx < Rобр обычно измеряют U, при измерении больших - Rx > Rобр измеряют U0
Электронный омметр Измеряется не ток, а падение напряжения. Либо на известном сопротивлении Rобр , либо на неизвестном. Rx = R0 /[U/Ux - 1] Rx = R0/[U/U0 - 1]
При измерении малых сопротивлений, когда Rx < Rобр обычно измеряют U, при измерении больших - Rx > Rобр измеряют U0
Слайд 130

6.1 Методы и приборы непосредственной оценки
Цифровой электронно-счетный омметр (фарадометр) Принцип: измерение интервала времени, равного постоянной времени цепи разряда конденсатора через резистор. При измерении Rx известный элемент С0, при измерении Сх — R0. Момент начала измерения t1 задается устройством управления, сбрасывающим электронный счетчик и переводящим ключ в положение разряда. Напряжение на конденсаторе Uc сравнивается с постоянным значением Ur .В момент, когда они оказываются равны, счет генерируемых импульсов прекращается.
Цифровой электронно-счетный омметр (фарадометр) Принцип: измерение интервала времени, равного постоянной времени цепи разряда конденсатора через резистор. При измерении Rx известный элемент С0, при измерении Сх — R0. Момент начала измерения t1 задается устройством управления, сбрасывающим электронный счетчик и переводящим ключ в положение разряда. Напряжение на конденсаторе Uc сравнивается с постоянным значением Ur .В момент, когда они оказываются равны, счет генерируемых импульсов прекращается.
Слайд 131
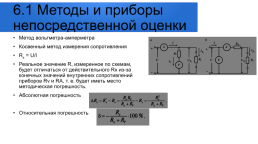
6.1 Методы и приборы непосредственной оценки
Метод вольтметра-амперметра Косвенный метод измерения сопротивления Rx = U/I Реальное значение R, измеренное по схемам, будет отличаться от действительного Rx из-за конечных значений внутренних сопротивлений приборов Rv и RA, т. е. будет иметь место методическая погрешность. Абсолютная погрешность Относительная погрешность
Метод вольтметра-амперметра Косвенный метод измерения сопротивления Rx = U/I Реальное значение R, измеренное по схемам, будет отличаться от действительного Rx из-за конечных значений внутренних сопротивлений приборов Rv и RA, т. е. будет иметь место методическая погрешность. Абсолютная погрешность Относительная погрешность
Слайд 132

6.1 Методы и приборы непосредственной оценки
Для определения С и L методом вольтметра-амперметра используется переменное напряжение известной частоты f. Емкость и индуктивность рассматриваются через величину полного сопротивления Z, для которой так же справедлив закон Ома.
Для определения С и L методом вольтметра-амперметра используется переменное напряжение известной частоты f. Емкость и индуктивность рассматриваются через величину полного сопротивления Z, для которой так же справедлив закон Ома.
Слайд 133

6.2 Методы и приборы сравнения
Измерительные мосты — приборы, служащие для измерения сопротивлений, емкостей и индуктивности, в основе которых заложен дифференциальный или нулевой метод. В последнем случае наблюдаем уравновешенный мост. Уравновешенный мост — четырехполюсник, питаемый от одного источника и имеющий две равнопотенциальные или близкопотенциальные точки, обнаруживаемые индикатором сравнения.
Условие балансировки моста — потенциалы точек б и г одинаковы.
Измерительные мосты — приборы, служащие для измерения сопротивлений, емкостей и индуктивности, в основе которых заложен дифференциальный или нулевой метод. В последнем случае наблюдаем уравновешенный мост. Уравновешенный мост — четырехполюсник, питаемый от одного источника и имеющий две равнопотенциальные или близкопотенциальные точки, обнаруживаемые индикатором сравнения.
Условие балансировки моста — потенциалы точек б и г одинаковы.
Слайд 134

6.2 Методы и приборы сравнения
Теория мостовых схем Полные сопротивления плеч моста имеют вид: Условие равновесия может быть выражено: Условие z1z2=z3z4 называют балансом амплитуд, а φ1 + φ2 =φ3 + φ4 - балансом фаз. Чувствительность мостовой схемы.
Теория мостовых схем Полные сопротивления плеч моста имеют вид: Условие равновесия может быть выражено: Условие z1z2=z3z4 называют балансом амплитуд, а φ1 + φ2 =φ3 + φ4 - балансом фаз. Чувствительность мостовой схемы.
Слайд 135
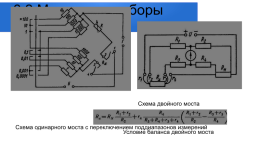
6.2 Методы и приборы сравнения
Схема двойного моста
Схема одинарного моста с переключением поддиапазонов измерений
Условие баланса двойного моста
Схема двойного моста
Схема одинарного моста с переключением поддиапазонов измерений
Условие баланса двойного моста
Слайд 136

6.2 Методы и приборы сравнения
В соответствии с условиями равновесия моста переменного тока, схемы мостов для измерения индуктивности, емкости и других сосредоточенных постоянных по переменному току, могут иметь различные варианты балансировочных плеч.
Слайд 137
6.2 Методы и приборы сравнения
Реальный конденсатор может быть представлен в виде соединения емкости и активного сопротивления, обуславливающего возникновение эквивалентных потерь. Отсюда tg δ = ωRC или tg δ = 1/ωRC В зависимости от величины угла различают малые потери и большие потери.
Реальный конденсатор может быть представлен в виде соединения емкости и активного сопротивления, обуславливающего возникновение эквивалентных потерь. Отсюда tg δ = ωRC или tg δ = 1/ωRC В зависимости от величины угла различают малые потери и большие потери.
Слайд 138

6.2 Методы и приборы сравнения
Схема моста для измерения емкости с малыми потерями
Для измерения емкости с большими потерями применяют мост с параллельным включением Rn и Сn , псокольку введение большого сопротивления последовательно уменьшает чувствительность моста
Схема моста для измерения емкости с малыми потерями
Для измерения емкости с большими потерями применяют мост с параллельным включением Rn и Сn , псокольку введение большого сопротивления последовательно уменьшает чувствительность моста
Слайд 139
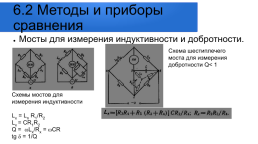
6.2 Методы и приборы сравнения
Мосты для измерения индуктивности и добротности.
Схема шестиплечего моста для измерения добротности Q< 1
Схемы мостов для измерения индуктивности Lx = Ln R1/R2 Lx = CR1R2 Q = ωLx/Rx = ωCR tg δ = 1/Q
Мосты для измерения индуктивности и добротности.
Схема шестиплечего моста для измерения добротности Q< 1
Схемы мостов для измерения индуктивности Lx = Ln R1/R2 Lx = CR1R2 Q = ωLx/Rx = ωCR tg δ = 1/Q
Слайд 140

6.3 Методы и приборы замещения
Резонансные измерители параметров элементов и цепей. Измерение параметров элементов и цепей на высоких частотах выполняют методом замещения в сочетании с явлением резонанса в цепи. Резонансный прибор состоит из генератора высокой частоты (ГВЧ), колебательного контура и индикатора резонанса — электронного вольтметра. Если измеряемую катушку включить параллельно известному конденсатору, то измеряя резонансную частоту, ее можно определить из выражения ω = 1/√LC Чтобы исключить влияние паразитных параметров, измерение выполняют дважды, реализуя тем самым метод замещения.
Резонансные измерители параметров элементов и цепей. Измерение параметров элементов и цепей на высоких частотах выполняют методом замещения в сочетании с явлением резонанса в цепи. Резонансный прибор состоит из генератора высокой частоты (ГВЧ), колебательного контура и индикатора резонанса — электронного вольтметра. Если измеряемую катушку включить параллельно известному конденсатору, то измеряя резонансную частоту, ее можно определить из выражения ω = 1/√LC Чтобы исключить влияние паразитных параметров, измерение выполняют дважды, реализуя тем самым метод замещения.
Слайд 141
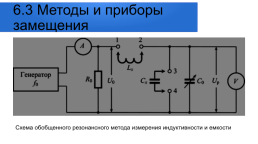
6.3 Методы и приборы замещения
Схема обобщенного резонансного метода измерения индуктивности и емкости
Схема обобщенного резонансного метода измерения индуктивности и емкости
Слайд 142

Метрологические основы, методы и техника измерений физических величин
Лекция № 7 Физические основы, методы и техника измерения неэлектрических величин
Преподаватель: Войнов Виктор Сергеевич
Лекция № 7 Физические основы, методы и техника измерения неэлектрических величин
Преподаватель: Войнов Виктор Сергеевич
Слайд 143
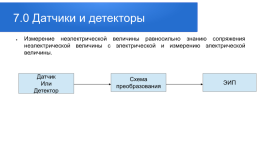
7.0 Датчики и детекторы
Измерение неэлектрической величины равносильно знанию сопряжения неэлектрической величины с электрической и измерению электрической величины.
Датчик Или Детектор
Схема преобразования
ЭИП
Измерение неэлектрической величины равносильно знанию сопряжения неэлектрической величины с электрической и измерению электрической величины.
Датчик Или Детектор
Схема преобразования
ЭИП
Слайд 144

7.0 Датчики и детекторы
Датчик (сенсор) — конструктивно обособленное устройство, содержащее один или несколько первичных измерительных преобразователей измерительного прибора или измерительной системы, преобразующий измеряемую величину в удобный для анализа сигнал. Детектор - первичный преобразователь, элемент измерительного, сигнального, регулирующего или управляющего устройства системы, преобразующий контролируемую величину в удобный для использования сигнал.
Датчик (сенсор) — конструктивно обособленное устройство, содержащее один или несколько первичных измерительных преобразователей измерительного прибора или измерительной системы, преобразующий измеряемую величину в удобный для анализа сигнал. Детектор - первичный преобразователь, элемент измерительного, сигнального, регулирующего или управляющего устройства системы, преобразующий контролируемую величину в удобный для использования сигнал.
Слайд 145
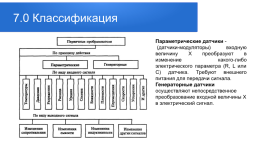
7.0 Классификация
Параметрические датчики - (датчики-модуляторы) входную величину X преобразуют в изменение какого-либо электрического параметра (R, L или C) датчика. Требуют внешнего питания для передачи сигнала. Генераторные датчики осуществляют непосредственное преобразование входной величины X в электрический сигнал.
Параметрические датчики - (датчики-модуляторы) входную величину X преобразуют в изменение какого-либо электрического параметра (R, L или C) датчика. Требуют внешнего питания для передачи сигнала. Генераторные датчики осуществляют непосредственное преобразование входной величины X в электрический сигнал.
Слайд 146

7.0 Характеристики датчиков
Диапазон входных значений — диапазон внешних воздействий, которые датчик может воспринять и преобразовать, не выходя за пределы допустимых погрешностей. Диапазон выходных значений — алгебраическая разность между электрическими выходными сигналами, измеренными при максимальной и минимальной величине внешнего воздействия. Погрешность — величина максимального расхождения между показаниями реального и идеального датчиков. Погрешность датчика можно также представить в виде разности между значением входного сигнала, вычисленным по выходному сигналу датчика, и реальным значением поданного сигнала. Чувствительность, разрешающая способность — величина минимального изменения входного сигнала, приводящая к появлению минимального изменения выходного сигнала датчика.
Диапазон входных значений — диапазон внешних воздействий, которые датчик может воспринять и преобразовать, не выходя за пределы допустимых погрешностей. Диапазон выходных значений — алгебраическая разность между электрическими выходными сигналами, измеренными при максимальной и минимальной величине внешнего воздействия. Погрешность — величина максимального расхождения между показаниями реального и идеального датчиков. Погрешность датчика можно также представить в виде разности между значением входного сигнала, вычисленным по выходному сигналу датчика, и реальным значением поданного сигнала. Чувствительность, разрешающая способность — величина минимального изменения входного сигнала, приводящая к появлению минимального изменения выходного сигнала датчика.
Слайд 147

7.0 Характеристики датчиков
Воспроизводимость — способность датчика при соблюдении одинаковых условий выдавать идентичные результаты. Воспроизводимость результатов определяется по максимальной разности выходных значений датчика, полученных в двух циклах калибровки. Гистерезис — разность значений выходного сигнала для одного и того же входного сигнала, полученных при его возрастании и убывании (трение, структурные особенности или изменения материалов). Передаточная функция — теоретическая функция, связывающая входной и выходной сигналы (может быть линейной или нелинейной).
Воспроизводимость — способность датчика при соблюдении одинаковых условий выдавать идентичные результаты. Воспроизводимость результатов определяется по максимальной разности выходных значений датчика, полученных в двух циклах калибровки. Гистерезис — разность значений выходного сигнала для одного и того же входного сигнала, полученных при его возрастании и убывании (трение, структурные особенности или изменения материалов). Передаточная функция — теоретическая функция, связывающая входной и выходной сигналы (может быть линейной или нелинейной).
Слайд 148

7.1 Метрологические характеристики датчиков температуры
Датчики температуры могут использовать несколько физических явлений: Изменение сопротивления вещества при изменении температуры (терморезисторы). Эффект Зеебека (термопары, термоэлектрические преобразователи). Измерение инфракрасного излучения (пирометры). Кварцевые преобразователи. Требования к эталону температуры: Диапазон: -200 ºС — 1000 ºС СКО S < 0,0005 ºC Неисключенная систематическая погрешность Θ = 0,0002 ºС
Датчики температуры могут использовать несколько физических явлений: Изменение сопротивления вещества при изменении температуры (терморезисторы). Эффект Зеебека (термопары, термоэлектрические преобразователи). Измерение инфракрасного излучения (пирометры). Кварцевые преобразователи. Требования к эталону температуры: Диапазон: -200 ºС — 1000 ºС СКО S < 0,0005 ºC Неисключенная систематическая погрешность Θ = 0,0002 ºС
Слайд 149

7.1.1 Терморезистор
Принцип действия — зависимость сопротивления материала от температуры. ТКС — температурный коэффициент сопротивления. Может быть + или - Металлический терморезистор из платины от 200 С до 0 С Rt = R0 [1+at+bt2+ct3 (t-100)] от 0 С до 650 С Rt = R0[1+at+bt2]
Сравнение темп. зависимостей разных датчиков
Чертеж платинового термистора
Принцип действия — зависимость сопротивления материала от температуры. ТКС — температурный коэффициент сопротивления. Может быть + или - Металлический терморезистор из платины от 200 С до 0 С Rt = R0 [1+at+bt2+ct3 (t-100)] от 0 С до 650 С Rt = R0[1+at+bt2]
Сравнение темп. зависимостей разных датчиков
Чертеж платинового термистора
Слайд 150
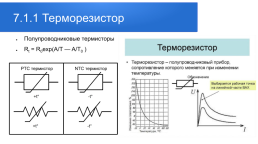
7.1.1 Терморезистор
Полупроводниковые термисторы Rt = R0exp(A/T — A/T0 )
Полупроводниковые термисторы Rt = R0exp(A/T — A/T0 )
Слайд 151

7.1.2 Термопара
Принцип действия — эффект Зеебека Суть термоэлектрическогоэффекта заключается в следующем: при соединении двух проводников из разнородных металлов на их границе раздела возникает контактная разность потенциалов, зависящая от рода металлов и температуры контакта. Если оба конца двух разнородных проводников соединить друг с другом и если температуры точек соединения будут одинаковы, то контактные разности потенциалов в этих точках соединений будут равны между собой, противоположно направлены и, следовательно, взаимно уравновешены. Если температуры точек соединения будут разными, то в цепи возникнет результирующая ЭДС , которая называется термоэлектродвижущей силой (термоЭДС).
T1 — известна; VAB — измеряется; Т2 — рассчитывается.
Принцип действия — эффект Зеебека Суть термоэлектрическогоэффекта заключается в следующем: при соединении двух проводников из разнородных металлов на их границе раздела возникает контактная разность потенциалов, зависящая от рода металлов и температуры контакта. Если оба конца двух разнородных проводников соединить друг с другом и если температуры точек соединения будут одинаковы, то контактные разности потенциалов в этих точках соединений будут равны между собой, противоположно направлены и, следовательно, взаимно уравновешены. Если температуры точек соединения будут разными, то в цепи возникнет результирующая ЭДС , которая называется термоэлектродвижущей силой (термоЭДС).
T1 — известна; VAB — измеряется; Т2 — рассчитывается.
Слайд 152

7.1.2 Термопара
Для наглядности
К вольтметру
К тому, температуру чего нужно измерить
Для наглядности
К вольтметру
К тому, температуру чего нужно измерить
Слайд 153
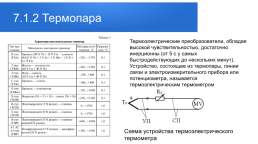
7.1.2 Термопара
Термоэлектрические преобразователи, обладая высокой чувствительностью, достаточно инерционны (от 5 с у самых быстродействующих до нескольких минут). Устройство, состоящее из термопары, линии связи и электроизмерительного прибора или потенциометра, называется термоэлектрическим термометром
Схема устройства термоэлектрического термометра
Термоэлектрические преобразователи, обладая высокой чувствительностью, достаточно инерционны (от 5 с у самых быстродействующих до нескольких минут). Устройство, состоящее из термопары, линии связи и электроизмерительного прибора или потенциометра, называется термоэлектрическим термометром
Схема устройства термоэлектрического термометра
Слайд 154

7.1.3 Пирометр
Пирометр — прибор для определения температуры бесконтактным способом, принцип действия которого основан на измерении температуры поверхности различных веществ путем определения интенсивности излучения.
Пирометры бывают 1) Оптическими (диапазон 700 — 10000) В основе — закон Планка 2) Цветовыми ( диапазон 900 — 3000) В основе — сравнение световых потоков монохроматического излучения 3) Радиационными (диапазон 20 — 4000) В основе — закон Стефана-Больцмана
Пирометр — прибор для определения температуры бесконтактным способом, принцип действия которого основан на измерении температуры поверхности различных веществ путем определения интенсивности излучения.
Пирометры бывают 1) Оптическими (диапазон 700 — 10000) В основе — закон Планка 2) Цветовыми ( диапазон 900 — 3000) В основе — сравнение световых потоков монохроматического излучения 3) Радиационными (диапазон 20 — 4000) В основе — закон Стефана-Больцмана
Слайд 155

7.2 Метрологические характеристики датчиков давления
Диапазон измеряемых давлений 10-6 (космос) до 1012 Па (подземные взрывы) Частотный диапазон от 0 до 50 кГц Наивысшая точность соответствует приведенной погрешности в 0.01% в диапазоне измерений от 0.5 Па до 250 МПа Давления ниже 10-4 измеряют с помощью тепловых и ионизационных вакууметров Для измерения в статическом режиме используются манометры с тензочувствительными преобразователями Для динамических измерений давления (акустика) используются пьезоэлектрические преобразователи в диапазоне 1-50 кГц
Диапазон измеряемых давлений 10-6 (космос) до 1012 Па (подземные взрывы) Частотный диапазон от 0 до 50 кГц Наивысшая точность соответствует приведенной погрешности в 0.01% в диапазоне измерений от 0.5 Па до 250 МПа Давления ниже 10-4 измеряют с помощью тепловых и ионизационных вакууметров Для измерения в статическом режиме используются манометры с тензочувствительными преобразователями Для динамических измерений давления (акустика) используются пьезоэлектрические преобразователи в диапазоне 1-50 кГц
Слайд 156

7.2.1 Тензорезистор
Принцип действия - зависимость электрического сопротивления проводника или полупроводника от его механической деформации (тензоэффект) ΔR/R = S * Δl/l — относительное изменение сопротивления пропорционально относительной деформации проводника В зависимости от используемого материала тензорезисторы делятся на металлические и полупроводниковые. Из металлических тензорезисторов наибольшее распространение получили проволочные, фольговые и пленочные
Структура проволочного преобразователя
Структура фольгового преобразователя
Принцип действия - зависимость электрического сопротивления проводника или полупроводника от его механической деформации (тензоэффект) ΔR/R = S * Δl/l — относительное изменение сопротивления пропорционально относительной деформации проводника В зависимости от используемого материала тензорезисторы делятся на металлические и полупроводниковые. Из металлических тензорезисторов наибольшее распространение получили проволочные, фольговые и пленочные
Структура проволочного преобразователя
Структура фольгового преобразователя
Слайд 157
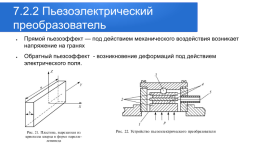
7.2.2 Пьезоэлектрический преобразователь
Прямой пьезоэффект — под действием механического воздействия возникает напряжение на гранях Обратный пьезоэффект - возникновение деформаций под действием электрического поля.
Прямой пьезоэффект — под действием механического воздействия возникает напряжение на гранях Обратный пьезоэффект - возникновение деформаций под действием электрического поля.
Слайд 158

7.3 Метрологические характеристики датчиков магнитного поля
Диапазон измерений — 10-14 — 102 Тл Частотный диапазон 0 — 10 МГц Физические основы: эффект Фарадея, эффект Холла, ядерно-магнитный резонанс
Диапазон измерений — 10-14 — 102 Тл Частотный диапазон 0 — 10 МГц Физические основы: эффект Фарадея, эффект Холла, ядерно-магнитный резонанс
Слайд 159

7.3.1 Измерительная катушка
Эффект Фарадея — возникновение ЭДС индукции в проводнике, находящемся в изменяющемся магнитном поле. Для постоянного поля можно изменять положение катушки.
Измеряемой величиной, строго говоря, является поток магнитного поля. Для определения индукции необходимо знать геометрические параметры катушки, для расчета индукции по известной величине потока.
Схема измерения магнитного потока индукционно-импульсным методом
Эффект Фарадея — возникновение ЭДС индукции в проводнике, находящемся в изменяющемся магнитном поле. Для постоянного поля можно изменять положение катушки.
Измеряемой величиной, строго говоря, является поток магнитного поля. Для определения индукции необходимо знать геометрические параметры катушки, для расчета индукции по известной величине потока.
Схема измерения магнитного потока индукционно-импульсным методом
Слайд 160
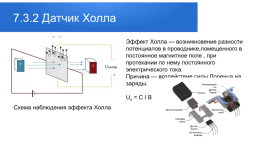
7.3.2 Датчик Холла
Эффект Холла — возникновение разности потенциалов в проводнике,помещенного в постоянное магнитное поле , при протекании по нему постоянного электрического тока. Причина — воздействие силы Лоренца на заряды. Ux = C I B
Схема наблюдения эффекта Холла
Эффект Холла — возникновение разности потенциалов в проводнике,помещенного в постоянное магнитное поле , при протекании по нему постоянного электрического тока. Причина — воздействие силы Лоренца на заряды. Ux = C I B
Схема наблюдения эффекта Холла
Слайд 161
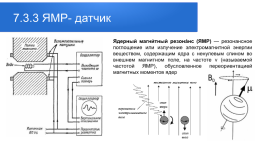
7.3.3 ЯМР- датчик
Ядерный магни́тный резона́нс (ЯМР) — резонансное поглощение или излучение электромагнитной энергии веществом, содержащим ядра с ненулевым спином во внешнем магнитном поле, на частоте ν (называемой частотой ЯМР), обусловленное переориентацией магнитных моментов ядер
Ядерный магни́тный резона́нс (ЯМР) — резонансное поглощение или излучение электромагнитной энергии веществом, содержащим ядра с ненулевым спином во внешнем магнитном поле, на частоте ν (называемой частотой ЯМР), обусловленное переориентацией магнитных моментов ядер
Слайд 162

7.4 Оптические датчики
Сущестет достаточно большое количество ФВ, связанных с оптическим излучением. Для удобства описания они делятся на две группы: светотехнические величины и энергетические.
Сущестет достаточно большое количество ФВ, связанных с оптическим излучением. Для удобства описания они делятся на две группы: светотехнические величины и энергетические.
Слайд 163

Шпаргалка по светотехническим величинам
Слайд 164

7.4 Оптические датчики
Параметрические оптические датчики Фотосопротивление Генераторные оптические датчики Фотодиод Фотоэлектронный умножитель (ФЭУ) Приборы с зарядовой связью (ПЗС)
Параметрические оптические датчики Фотосопротивление Генераторные оптические датчики Фотодиод Фотоэлектронный умножитель (ФЭУ) Приборы с зарядовой связью (ПЗС)
Слайд 165

7.4.1 Фотосопротивление
Принцип: при освещении полупроводника его электрическое сопротивление меняется. Явление называется фотопроводимостью. В отсутствии освещения при комнатной температуре по фоторезистору будет протекать темновой ток. В зависимости от материала, из которого изготовлен фоторезистор,значительно меняется его спектральная чувствительность. К достоинствам фотосопротивлений относятся: высокая фоточувствительность, большой срок службы, малые размеры, простота изготовления, возможность выбора фотосопротивления для нужного интервала длин волн, в частности и для инфракрасной области. К недостаткам относятся: отсутствие прямой пропорциональности между током в цепи и интенсивностью освещения, влияние на величину сопротивления температуры окружающей среды, инерционность. Последний недостаток объясняется тем, что рекомбинация электронов и дырок после прекращения освещения происходит за время от одной до сотен микросекунд, поэтому при быстрых изменениях светового потока проводимость полупроводника не успевает следовать за этими изменениями.
Принцип: при освещении полупроводника его электрическое сопротивление меняется. Явление называется фотопроводимостью. В отсутствии освещения при комнатной температуре по фоторезистору будет протекать темновой ток. В зависимости от материала, из которого изготовлен фоторезистор,значительно меняется его спектральная чувствительность. К достоинствам фотосопротивлений относятся: высокая фоточувствительность, большой срок службы, малые размеры, простота изготовления, возможность выбора фотосопротивления для нужного интервала длин волн, в частности и для инфракрасной области. К недостаткам относятся: отсутствие прямой пропорциональности между током в цепи и интенсивностью освещения, влияние на величину сопротивления температуры окружающей среды, инерционность. Последний недостаток объясняется тем, что рекомбинация электронов и дырок после прекращения освещения происходит за время от одной до сотен микросекунд, поэтому при быстрых изменениях светового потока проводимость полупроводника не успевает следовать за этими изменениями.
Слайд 166
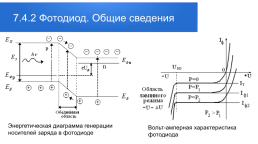
7.4.2 Фотодиод. Общие сведения
Энергетическая диаграмма генерации носителей заряда в фотодиоде
Вольт-амперная характеристика фотодиода
Энергетическая диаграмма генерации носителей заряда в фотодиоде
Вольт-амперная характеристика фотодиода
Слайд 167
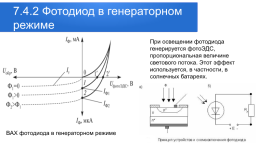
7.4.2 Фотодиод в генераторном режиме
При освещении фотодиода генерируется фотоЭДС, пропорциональная величине светового потока. Этот эффект используется, в частности, в солнечных батареях.
ВАХ фотодиода в генераторном режиме
При освещении фотодиода генерируется фотоЭДС, пропорциональная величине светового потока. Этот эффект используется, в частности, в солнечных батареях.
ВАХ фотодиода в генераторном режиме
Слайд 168
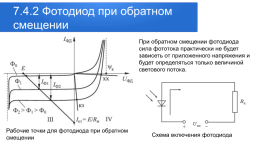
7.4.2 Фотодиод при обратном смещении
При обратном смещении фотодиода сила фототока практически не будет зависеть от приложенного напряжения и будет определяться только величиной светового потока.
Рабочие точки для фотодиода при обратном смещении
Схема включения фотодиода
При обратном смещении фотодиода сила фототока практически не будет зависеть от приложенного напряжения и будет определяться только величиной светового потока.
Рабочие точки для фотодиода при обратном смещении
Схема включения фотодиода
Слайд 169

7.4.3 Фотоэлектронный умножитель
Принцип действия: внешний фотоэффект. Фотон выбивает с поверхности фотокатода фотоэлектрон. Под действием ускоряющего напряжения между динодами фотоэлектрон выбивает с поверхности первого динода вторичные электроны (вторичная эмиссия). Количество динодов и коэффициент размножения влияют на итоговую величину импульса тока. Число импульсов тока пропорционально числу фотонов.
Устройство ФЭУ
Принцип действия: внешний фотоэффект. Фотон выбивает с поверхности фотокатода фотоэлектрон. Под действием ускоряющего напряжения между динодами фотоэлектрон выбивает с поверхности первого динода вторичные электроны (вторичная эмиссия). Количество динодов и коэффициент размножения влияют на итоговую величину импульса тока. Число импульсов тока пропорционально числу фотонов.
Устройство ФЭУ
Слайд 170

7.4.3 ФЭУ на лавинном фотодиоде
Принцип действия: при подаче сильного обратного смещения (близкого к значению лавинного пробоя) происходит усиление фототока за счет ударной ионизации (лавинного умножения) генерированных светом носителей заряда. Схема включения аналогична схеме включения фотодиода при обратном смещении.
Структура лавинного фотодиода
Принцип действия: при подаче сильного обратного смещения (близкого к значению лавинного пробоя) происходит усиление фототока за счет ударной ионизации (лавинного умножения) генерированных светом носителей заряда. Схема включения аналогична схеме включения фотодиода при обратном смещении.
Структура лавинного фотодиода
Слайд 171

7.5 Датчики перемещения
В процессе линейного или углового перемещения объект изменяет свое положение в пространстве по отношению к первоначальному положению, находящемуся от него соответственно на каком-либо расстоянии или под каким-либо углом. Датчики линейных перемещений служат для измерения расстояний до объектов, а датчики угловых перемещений – для измерения углов поворота вращающихся объектов Зачастую такие датчики являются параметрическими, с изменяющимися величинами R, L и С.
В процессе линейного или углового перемещения объект изменяет свое положение в пространстве по отношению к первоначальному положению, находящемуся от него соответственно на каком-либо расстоянии или под каким-либо углом. Датчики линейных перемещений служат для измерения расстояний до объектов, а датчики угловых перемещений – для измерения углов поворота вращающихся объектов Зачастую такие датчики являются параметрическими, с изменяющимися величинами R, L и С.
Слайд 172
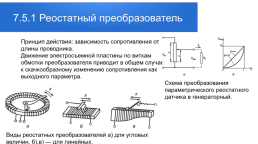
7.5.1 Реостатный преобразователь
Принцип действия: зависимость сопротивления от длины проводника. Движение электросъемной пластины по виткам обмотки преобразователя приводит в общем случае к скачкообразному изменению сопротивления как выходного параметра.
Схема преобразования параметрического реостатного датчика в генераторный.
Виды реостатных преобразователей а) для угловых величин, б),в) — для линейных.
Принцип действия: зависимость сопротивления от длины проводника. Движение электросъемной пластины по виткам обмотки преобразователя приводит в общем случае к скачкообразному изменению сопротивления как выходного параметра.
Схема преобразования параметрического реостатного датчика в генераторный.
Виды реостатных преобразователей а) для угловых величин, б),в) — для линейных.
Слайд 173
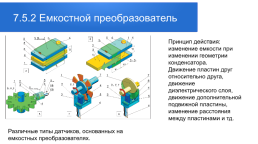
7.5.2 Емкостной преобразователь
Принцип действия: изменение емкости при изменении геометрии конденсатора. Движение пластин друг относительно друга, движение диэлектрического слоя, движение дополнительной подвижной пластины, изменение расстояния между пластинами и тд.
Различные типы датчиков, основанных на емкостных преобразователях.
Принцип действия: изменение емкости при изменении геометрии конденсатора. Движение пластин друг относительно друга, движение диэлектрического слоя, движение дополнительной подвижной пластины, изменение расстояния между пластинами и тд.
Различные типы датчиков, основанных на емкостных преобразователях.
Слайд 174

7.5.2 Емкостной преобразователь
Основными достоинствами емкостных преобразователей являются высокая чувствительность (при использовании измерительных схем с резонансными контурами реагируют на перемещения порядка 10 –7 мм), простота конструкции, незначительные размеры и вес и малая инерционность. К их недостаткам относятся подверженность влиянию внешних электрических полей, паразитных емкостей, температуры и влажности окружающей среды.
Основными достоинствами емкостных преобразователей являются высокая чувствительность (при использовании измерительных схем с резонансными контурами реагируют на перемещения порядка 10 –7 мм), простота конструкции, незначительные размеры и вес и малая инерционность. К их недостаткам относятся подверженность влиянию внешних электрических полей, паразитных емкостей, температуры и влажности окружающей среды.
Слайд 175

7.5.3 Индуктивные преобразователи
Принцип действия: зависимость собственной или взаимной индуктивностей обмоток, расположенных на магнитопроводе, от геометрических размеров и магнитного состояния отдельных элементов конструкции, а также в случае взаимной индуктивности от взаимного положения обмоток. Перемещая подвижную часть (якорь) 1 сердечника относительно неподвижной 2, можно изменять длину воздушного зазора δ (вертикальное перемещение якоря) или площадь поперечного сечения S (горизонтальное перемещение якоря).
Принцип действия: зависимость собственной или взаимной индуктивностей обмоток, расположенных на магнитопроводе, от геометрических размеров и магнитного состояния отдельных элементов конструкции, а также в случае взаимной индуктивности от взаимного положения обмоток. Перемещая подвижную часть (якорь) 1 сердечника относительно неподвижной 2, можно изменять длину воздушного зазора δ (вертикальное перемещение якоря) или площадь поперечного сечения S (горизонтальное перемещение якоря).
Слайд 176
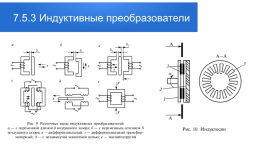
7.5.3 Индуктивные преобразователи
Слайд 177

7.6 Датчики скорости
Выделяют линейную и угловую скорости, понимая под этим,насколько быстро объект передвигается по прямой или насколько быстро вращается. Линейную скорость можно определить, измеряя расстояние, на которое переместился исследуемый объект относительно эталонного объекта, входящего в состав датчика. Угловые скорости измеряют тахометрами. При этом либо непосредственно определяют частоту вращения, либо сравнивают ее со стабильной эталонной частотой. Популярны тахогенераторы постоянного и переменного тока. Многие линейные датчики скорости используют принцип магнитной индукции.
Выделяют линейную и угловую скорости, понимая под этим,насколько быстро объект передвигается по прямой или насколько быстро вращается. Линейную скорость можно определить, измеряя расстояние, на которое переместился исследуемый объект относительно эталонного объекта, входящего в состав датчика. Угловые скорости измеряют тахометрами. При этом либо непосредственно определяют частоту вращения, либо сравнивают ее со стабильной эталонной частотой. Популярны тахогенераторы постоянного и переменного тока. Многие линейные датчики скорости используют принцип магнитной индукции.
Слайд 178

7.6 Индукционный датчик скорости
Принцип действия: закон электромагнитной индукции. В соответствии с этим законом при изменении потока ψ, сцепленного с катушкой с числом витков w, в последней индуцируется ЭДС самоиндукции e,пропорциональное скорости изменения этого потока и противодействующее ему в соответствии с выражением е = –dψ/dt = –wdФ/dt, где Ф — магнитный поток, сцепленный с катушкой. Данный принцип действия можно реализовать либо путем перемещения (линейного или углового) катушки в зазоре постоянного магнита, либо при механическом модулировании магнитного потока постоянного магнита (например, изменяя величину воздушного зазора в цепи магнитопровода при неподвижной катушке).
Принцип действия: закон электромагнитной индукции. В соответствии с этим законом при изменении потока ψ, сцепленного с катушкой с числом витков w, в последней индуцируется ЭДС самоиндукции e,пропорциональное скорости изменения этого потока и противодействующее ему в соответствии с выражением е = –dψ/dt = –wdФ/dt, где Ф — магнитный поток, сцепленный с катушкой. Данный принцип действия можно реализовать либо путем перемещения (линейного или углового) катушки в зазоре постоянного магнита, либо при механическом модулировании магнитного потока постоянного магнита (например, изменяя величину воздушного зазора в цепи магнитопровода при неподвижной катушке).
Слайд 179
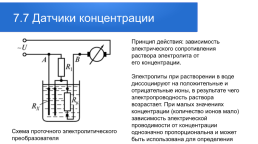
7.7 Датчики концентрации
Принцип действия: зависимость электрического сопротивления раствора электролита от его концентрации. Электролиты при растворении в воде диссоциируют на положительные и отрицательные ионы, в результате чего электропроводность раствора возрастает. При малых значениях концентрации (количество ионов мало) зависимость электрической проводимости от концентрации однозначно пропорциональна и может быть использована для определения последней.
Схема проточного электролитического преобразователя
Принцип действия: зависимость электрического сопротивления раствора электролита от его концентрации. Электролиты при растворении в воде диссоциируют на положительные и отрицательные ионы, в результате чего электропроводность раствора возрастает. При малых значениях концентрации (количество ионов мало) зависимость электрической проводимости от концентрации однозначно пропорциональна и может быть использована для определения последней.
Схема проточного электролитического преобразователя
Слайд 180
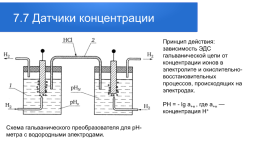
7.7 Датчики концентрации
Принцип действия: зависимость ЭДС гальванической цепи от концентрации ионов в электролите и окислительно-восстановительных процессов, происходящих на электродах. PH = - lg a+н , где a+н — концентрация Н+
Схема гальванического преобразователя для рН-метра с водородными электродами.
Принцип действия: зависимость ЭДС гальванической цепи от концентрации ионов в электролите и окислительно-восстановительных процессов, происходящих на электродах. PH = - lg a+н , где a+н — концентрация Н+
Схема гальванического преобразователя для рН-метра с водородными электродами.
Слайд 181

Метрологические основы, методы и техника измерений физических величин
Лекция №8 Подготовка измерительного эксперимента и обработка результатов измерений
Преподаватель: Войнов Виктор Сергеевич
Лекция №8 Подготовка измерительного эксперимента и обработка результатов измерений
Преподаватель: Войнов Виктор Сергеевич
Слайд 182

8.1 Подготовка измерительного эксперимента
Последовательность действий: Составление примерной, доопытной модели объекта Обоснование необходимой точности эксперимента Выработка методики проведения эксперимента Выбор средств измерений
Последовательность действий: Составление примерной, доопытной модели объекта Обоснование необходимой точности эксперимента Выработка методики проведения эксперимента Выбор средств измерений
Слайд 183

8.1 Подготовка измерительного эксперимента
Факторы, влияющие на выбор СИ Воздействие СИ на объект измерения Неполная адекватность принятой модели объекта измерения Погрешности, вносимые средствами измерений Пределы измерений Частотный диапазон измерений
Факторы, влияющие на выбор СИ Воздействие СИ на объект измерения Неполная адекватность принятой модели объекта измерения Погрешности, вносимые средствами измерений Пределы измерений Частотный диапазон измерений
Слайд 184

8.2 Обработка результатов измерений
Классификация измерений: Прямые — искомое значение ФВ получают непосредственно, Косвенные — определение искомого значения ФВ на основании результатов прямых измерений других ФВ, функционально связанных с искомой, Совместные — проводимые одновременно измерения двух или нескольких неодноименных величин, для определения зависимости между ними Совокупные — проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения ФВ определяют путем решения системы уравнений, характеризующих значения этих величин в различных сочетаниях.
Классификация измерений: Прямые — искомое значение ФВ получают непосредственно, Косвенные — определение искомого значения ФВ на основании результатов прямых измерений других ФВ, функционально связанных с искомой, Совместные — проводимые одновременно измерения двух или нескольких неодноименных величин, для определения зависимости между ними Совокупные — проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения ФВ определяют путем решения системы уравнений, характеризующих значения этих величин в различных сочетаниях.
Слайд 185

8.2.1 Случайные погрешности и способы их описания
Погрешность Δ = Δо+Δс наиболее полно характеризуется функцией распределения вероятности F(Δ), орпеделяющей вероятность появления того,что случайная погрешность Δi в i-м опыте окажется меньше некоторого значения Δ: F(Δ) = P[Δi ≤ Δ] = P{-∞<Δi<Δ} Плотность распределения вероятностей f(Δ) F(Δ) = ∫ f(Δ)d(Δ) Значение f(Δ)d(Δ) есть элемент вероятности , равный площади прямоугольника с основанием d(Δ) и абциссами Δ1 и Δ2 , называемыми квантилями, Квантиль — значение, которое случайная величина не превышает с заданной вероятностью. Доверительный интервал случайной погрешности, ограниченной квантилями Δ1 и Δ2 охватывает вероятность Р всех возможных значений случайной погрешности, а q=1-P остается за границами интервала (q — уровень значимости)
Погрешность Δ = Δо+Δс наиболее полно характеризуется функцией распределения вероятности F(Δ), орпеделяющей вероятность появления того,что случайная погрешность Δi в i-м опыте окажется меньше некоторого значения Δ: F(Δ) = P[Δi ≤ Δ] = P{-∞<Δi<Δ} Плотность распределения вероятностей f(Δ) F(Δ) = ∫ f(Δ)d(Δ) Значение f(Δ)d(Δ) есть элемент вероятности , равный площади прямоугольника с основанием d(Δ) и абциссами Δ1 и Δ2 , называемыми квантилями, Квантиль — значение, которое случайная величина не превышает с заданной вероятностью. Доверительный интервал случайной погрешности, ограниченной квантилями Δ1 и Δ2 охватывает вероятность Р всех возможных значений случайной погрешности, а q=1-P остается за границами интервала (q — уровень значимости)
Слайд 186

8.2.1 Случайные погрешности и способы их описания
Систематическая погрешность — отклонение математического ожидания mx результатов наблюдений от истинного значение А измеряемой величины Δс = mx — A = ∫xf(x)dx — A Случайная погрешность Δº — разность между результатом единичного измерения и математическим ожиданием результатов Δº = x — M[x] = x - ∫xf(x)dx Математическое ожидание погрешности равно математическому ожиданию систематической составляющей, поскольку математическое ожидание случайной погрешности всегда равно нулю M[Δ] = M[Δc] Центральный момент 2-го порядка — дисперсия D[x] = M[(x-mx)2 ] = ∫Δ2f(Δ)dΔ CКО δ[x] = δ[Δ]+ √D[x]
Систематическая погрешность — отклонение математического ожидания mx результатов наблюдений от истинного значение А измеряемой величины Δс = mx — A = ∫xf(x)dx — A Случайная погрешность Δº — разность между результатом единичного измерения и математическим ожиданием результатов Δº = x — M[x] = x - ∫xf(x)dx Математическое ожидание погрешности равно математическому ожиданию систематической составляющей, поскольку математическое ожидание случайной погрешности всегда равно нулю M[Δ] = M[Δc] Центральный момент 2-го порядка — дисперсия D[x] = M[(x-mx)2 ] = ∫Δ2f(Δ)dΔ CКО δ[x] = δ[Δ]+ √D[x]
Слайд 187

8.2.2 Наиболее известные распределения случайных величин
Слайд 188

8.2.2 Наиболее известные распределения случайных величин
Примеры распределения Пирсона с различными степенями свободы
Примеры распределения Пирсона с различными степенями свободы
Слайд 189
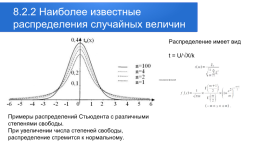
8.2.2 Наиболее известные распределения случайных величин
Распределение имеет вид t = U/√X/k
Примеры распределений Стьюдента с различными степенями свободы. При увеличении числа степеней свободы, распределение стремится к нормальному.
Распределение имеет вид t = U/√X/k
Примеры распределений Стьюдента с различными степенями свободы. При увеличении числа степеней свободы, распределение стремится к нормальному.
Слайд 190

8.2.3 Композиция законов распределения
Закон распределения суммы N независимых случайных величин, распределенных по нормальному закону, также является нормальным. mΔ = mΔ1 + mΔ2 +...+ mΔn σ = √σ1 + σ2 Δ= zσ Случайные величины независимы, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.
Закон распределения суммы N независимых случайных величин, распределенных по нормальному закону, также является нормальным. mΔ = mΔ1 + mΔ2 +...+ mΔn σ = √σ1 + σ2 Δ= zσ Случайные величины независимы, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.
Слайд 191
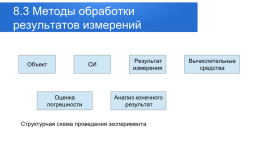
8.3 Методы обработки результатов измерений
Объект
СИ
Результат измерения
Вычислительные средства
Оценка погрешности
Анализ конечного результат
Структурная схема проведения эксперимента
Слайд 192

8.3.1 Равноточные многократные измерения
ГОСТ — 8.736 - 2011 Равноточные измерения — ряд измерений какой- либо величины, выполненных одинаковыми по точности СИ в одних и тех же условиях с одинаковой тщательностью. Многократное измерение — измерение ФВ одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящих из ряда однократных измерений. Проверка гипотезы нормального распределения зависит от числа измерений n. n>50 - критерий Пирсона, Колмогорова или Мизеса-Смирнова 15< n<50 — с помощью двух составных критериев
ГОСТ — 8.736 - 2011 Равноточные измерения — ряд измерений какой- либо величины, выполненных одинаковыми по точности СИ в одних и тех же условиях с одинаковой тщательностью. Многократное измерение — измерение ФВ одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящих из ряда однократных измерений. Проверка гипотезы нормального распределения зависит от числа измерений n. n>50 - критерий Пирсона, Колмогорова или Мизеса-Смирнова 15< n<50 — с помощью двух составных критериев
Слайд 193

8.3.2 Неравноточные измерения
Неравноточные измерения — ряд измерений какой-либо величины, различающимися по точности СИ и или в разных условиях. Наиболее достоверным является средневзвешенное значение
Неравноточные измерения — ряд измерений какой-либо величины, различающимися по точности СИ и или в разных условиях. Наиболее достоверным является средневзвешенное значение
Слайд 194

8.3.3 Косвенные измерения
Слайд 195

8.3.4 Совокупные и совместные измерения
Искомые величины рассчитывают по системе уравнений, связывающих их с некоторыми другими величинами, измеряемыми прямыми или косвенными способами. Fi (A,B,C … xi, yi, zi) = li При решении системы уравнений руководствуются методом наименьших квадратов
Искомые величины рассчитывают по системе уравнений, связывающих их с некоторыми другими величинами, измеряемыми прямыми или косвенными способами. Fi (A,B,C … xi, yi, zi) = li При решении системы уравнений руководствуются методом наименьших квадратов
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
