Презентация - Uniform circular motion

Uniform Circular Motion
© 2015 Pearson Education, Inc.

UNIFORM CIRCULAR MOTION (UCM)
Motion of an object along a circular path at a constant speed.

Period, Frequency, and Speed
The time interval it takes an object to go around a circle one time is called the period of the motion. We can specify circular motion by its frequency, the number of revolutions per second: The SI unit of frequency is inverse seconds, or s–1.
© 2015 Pearson Education, Inc.

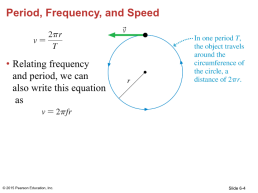
Period, Frequency, and Speed
Relating frequency and period, we can also write this equation as
© 2015 Pearson Education, Inc.

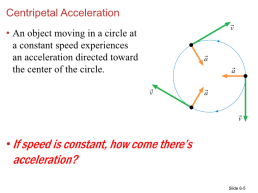
Centripetal Acceleration
An object moving in a circle at a constant speed experiences an acceleration directed toward the center of the circle. If speed is constant, how come there’s acceleration?

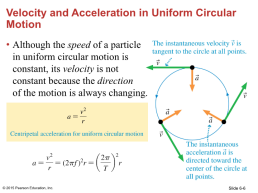
Velocity and Acceleration in Uniform Circular Motion
Although the speed of a particle in uniform circular motion is constant, its velocity is not constant because the direction of the motion is always changing.
© 2015 Pearson Education, Inc.

Example 1. Spinning some tunes
An audio CD has a diameter of 120 mm and spins at up to 540 rpm. When a CD is spinning at its maximum rate, how much time is required for one revolution? If a speck of dust rides on the outside edge of the disk, how fast is it moving? What is the acceleration?
© 2015 Pearson Education, Inc.

Dynamics of Uniform Circular Motion
© 2015 Pearson Education, Inc.

Dynamics of Uniform Circular Motion
Riders traveling around on a circular carnival ride are accelerating, as we have seen:
© 2015 Pearson Education, Inc.

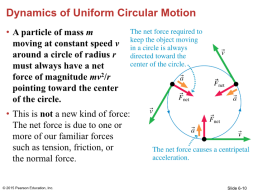
Dynamics of Uniform Circular Motion
A particle of mass m moving at constant speed v around a circle of radius r must always have a net force of magnitude mv2/r pointing toward the center of the circle. This is not a new kind of force: The net force is due to one or more of our familiar forces such as tension, friction, or the normal force.
© 2015 Pearson Education, Inc.

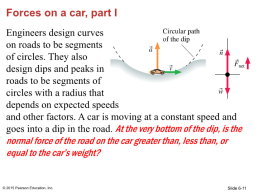
Forces on a car, part I
Engineers design curves on roads to be segments of circles. They also design dips and peaks in roads to be segments of circles with a radius that depends on expected speeds and other factors. A car is moving at a constant speed and goes into a dip in the road. At the very bottom of the dip, is the normal force of the road on the car greater than, less than, or equal to the car’s weight?
© 2015 Pearson Education, Inc.

Forces on a car, part I (cont.)
The car is accelerating, even though it is moving at a constant speed, because its direction is changing. When the car is at the bottom of the dip, the center of its circular path is directly above it and so its acceleration vector points straight up. The free-body diagram identifies the only two forces acting on the car as the normal force, pointing upward, and its weight, pointing downward.
© 2015 Pearson Education, Inc.

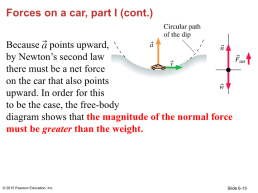
Forces on a car, part I (cont.)
Because points upward, by Newton’s second law there must be a net force on the car that also points upward. In order for this to be the case, the free-body diagram shows that the magnitude of the normal force must be greater than the weight.
© 2015 Pearson Education, Inc.

Problem-Solving Strategy Circular Dynamics Problems
© 2015 Pearson Education, Inc.

Problem-Solving Strategy Circular Dynamics Problems (cont.)
© 2015 Pearson Education, Inc.

Example Problem
In the track and field event known as the hammer throw, an athlete spins a heavy mass in a circle at the end of a chain. The mass flies off in a parabolic arc; the winner is the one who gets the maximum distance. The “hammer” is a mass of 7.3 kg at the end of a 1.2-m chain. A world-class thrower can obtain a speed of 29 m/s. If an athlete swings the mass in a horizontal circle, what is the tension in the chain?
© 2015 Pearson Education, Inc.

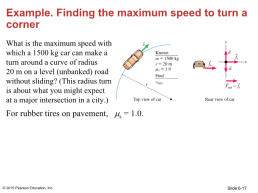
Example. Finding the maximum speed to turn a corner
What is the maximum speed with which a 1500 kg car can make a turn around a curve of radius 20 m on a level (unbanked) road without sliding? (This radius turn is about what you might expect at a major intersection in a city.) For rubber tires on pavement, s = 1.0.
© 2015 Pearson Education, Inc.

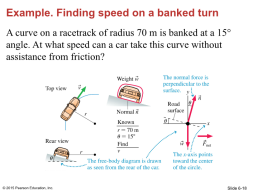
Example. Finding speed on a banked turn
A curve on a racetrack of radius 70 m is banked at a 15° angle. At what speed can a car take this curve without assistance from friction?
© 2015 Pearson Education, Inc.

Example Problem
A level curve on a country road has a radius of 150 m. What is the maximum speed at which this curve can be safely negotiated on a rainy day when the coefficient of friction between the tires on a car and the road is 0.40?
© 2015 Pearson Education, Inc.

QUICK CHECK
© 2015 Pearson Education, Inc.

A softball pitcher is throwing a pitch. At the instant shown, the ball is moving in a circular arc at a steady speed. At this instant, the acceleration is Directed up. Directed down. Directed left. Directed right. Zero.
© 2015 Pearson Education, Inc.

For uniform circular motion, the acceleration Is parallel to the velocity. Is directed toward the center of the circle. Is larger for a larger orbit at the same speed. Is always due to gravity. Is always negative.
© 2015 Pearson Education, Inc.

When a car turns a corner on a level road, which force provides the necessary centripetal acceleration? Friction Normal force Gravity Tension Air resistance
© 2015 Pearson Education, Inc.

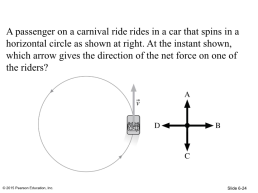
A passenger on a carnival ride rides in a car that spins in a horizontal circle as shown at right. At the instant shown, which arrow gives the direction of the net force on one of the riders?
© 2015 Pearson Education, Inc.

A ball at the end of a string is being swung in a horizontal circle. The ball is accelerating because The speed is changing. The direction is changing. The speed and the direction are changing. The ball is not accelerating.
© 2015 Pearson Education, Inc.

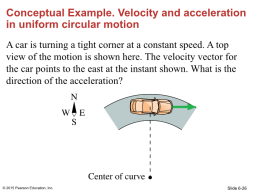
Conceptual Example. Velocity and acceleration in uniform circular motion
A car is turning a tight corner at a constant speed. A top view of the motion is shown here. The velocity vector for the car points to the east at the instant shown. What is the direction of the acceleration?
© 2015 Pearson Education, Inc.

A ball at the end of a string is being swung in a horizontal circle. What force is producing the centripetal acceleration of the ball? Gravity Air resistance Normal force Tension in the string
© 2015 Pearson Education, Inc.

A coin is rotating on a turntable; it moves without sliding. At the instant shown, suppose the frictional force disappeared. In what direction would the coin move?
© 2015 Pearson Education, Inc.

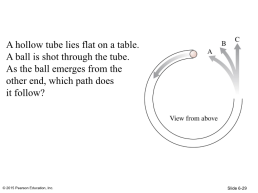
A hollow tube lies flat on a table. A ball is shot through the tube. As the ball emerges from the other end, which path does it follow?
© 2015 Pearson Education, Inc.