Презентация - Units of measurement in physics

Physics- study of motion, forces, energy, matter, heat, sound, light, and the composition of atoms
Units of Measurement In 1960, an international committee came up with a system of standard units called the SI system (Système International) of units Length = meter 1983 – meter = the distance traveled by light in a vacuum during an interval of 1/299792458 second Mass = kilogram Mass is a quantity used to measure the resistance to a change in state of motion of an object Time = second KNOW YOUR METRIC PREFIXES!!!

Building Blocks of Matter
Democritus – Greek Philosopher  the atom (atomos means “not sliceable” in Greek) Atoms – Protons – + charged; in nucleus; the # of protons in a nucleus determines what element the material is Neutrons – 0 charge; in nucleus; similar mass to proton; one purpose is to serve as “glue” to help hold protons together Protons and Neutrons are now thought to be composed of particles called quarks

Significant Figures
Significant Figures- the #’s recorded in a measurement ANY measurement always has some degree of uncertainty DO NOT ROUND OFF RANDOMLY!!! Always estimate one additional decimal place   If a measurement happens to be right on the line, add a 0 in the last decimal place  2.50 m

How many significant digits are in the following numbers?
0.0084 200.010 5200 8.60 x 10-3 150.0 0.00005 46.27
2 Significant Digits 6 Significant Digits 2 Significant Digits 3 Significant Digits 4 Significant Digits 1 Significant Digit 4 Significant Digits

Accuracy vs. Precision
Accuracy = how correct you are Precision = how repeatable something is Significant Figures: the #s recorded in a measurement (all the certain #s plus the 1st uncertain #) Calculations with Sig Figs-

Multiplication or Division the # of sig figs in the answer is the same as that in the measurement with the smallest # of sig figs 2.3 x 1.489 = 3.4247 (on your calculator) what is the answer to the problem? 3.4 (because 2.3 only has 2 s.f.) 7.93/4.8367 = 1.6395476 (on your calculator) what is the answer to the problem? 1.64 (because 7.93 only has 3 s.f.)

Addition or Subtraction
the limiting term is the one with the smallest # of decimal places to the right of the decimal 12.11 + 18.0 + 1.013 = 31.123 (on your calculator) answer? 31.1 (because 18.0 only has 1 place past the decimal) 1.013 – 12.11 = -11.097 (on your calculator) answer? -11.10 (because 12.11 only has 2 places past the decimal)

REVIEW
0.0677 cm + 48.1 cm + 82.7655 cm (2.51 m/s) x (0.83 s) (68 meters) ÷ (8.82 seconds) 43.832 liters – 29.28 liters

Dimensional Analysis
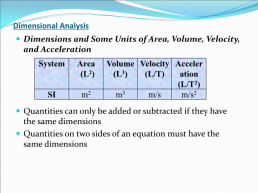
Dimensions and Some Units of Area, Volume, Velocity, and Acceleration Quantities can only be added or subtracted if they have the same dimensions Quantities on two sides of an equation must have the same dimensions
System.Area (L2).Volume (L3).Velocity (L/T).Acceleration (L/T2)
SI.m2.m3.m/s.m/s2

Conversion of Units
start with the given number in the upper left corner place the conversion factor so that the units you do not want cancel keep placing conversion factors until you get to the units that you want Solve the problem 1. If a car is traveling at a speed of 28.0 m/s, is it exceeding the speed limit of 65.0 mi/hr? so the car is not exceeding the speed limit

2. Convert 43 km/hr to m/s 12 m/s 3. The tallest man on record was Robert Wadlow, who had a height of 2.72 m. Express his height in feet. 8.92 ft 4. Express the speed limit of 65 miles/hr in terms of meters/second. 29 m/s

Mathematical Notation
α denotes a proportionality < less than > greater than ≈ approximately equal ≡ defined as ∆x change in the quantity x ∆x = xf – xi xf = final position; xi = initial position ∑ sum of absolute value of x

Coordinate Systems and Frames of Reference
A coordinate system used to specify locations in space consist of A fixed reference point O, called the origin A set of specified axes or directions with an appropriate scale and labels on the axes Instructions that tell us how to label a point in space relative to the origin and axes We will usually use the Cartesian coordinate system (the one that you are used to in math

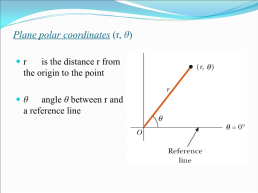
Plane polar coordinates (r, θ)
r is the distance r from the origin to the point θ angle θ between r and a reference line

Trigonometry
The portion of mathematics that is based on the special properties of right triangles SOHCAHTOA Sine = Opposite/Hypotenuse Cosine = Adjacent/Hypotenuse Tangent = Opposite/Adjacent Pythagorean Theorem  a2 + b2 = c2 Inverse relationships  What angle has a sine of 0.866?  sin-1(0.866) = 60o What angle has a tangent of 0.400  tan-1(0.400) = 21.8o

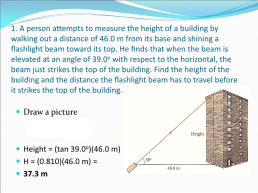
1. A person attempts to measure the height of a building by walking out a distance of 46.0 m from its base and shining a flashlight beam toward its top. He finds that when the beam is elevated at an angle of 39.0o with respect to the horizontal, the beam just strikes the top of the building. Find the height of the building and the distance the flashlight beam has to travel before it strikes the top of the building.
Draw a picture Height = (tan 39.0o)(46.0 m) H = (0.810)(46.0 m) = 37.3 m

For the distance the flashlight beam has to travel to reach the top of the building, Use Pythagorean Theorem a2 + b2 = c2

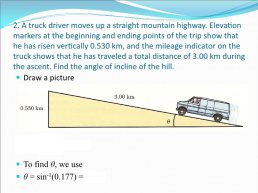
2. A truck driver moves up a straight mountain highway. Elevation markers at the beginning and ending points of the trip show that he has risen vertically 0.530 km, and the mileage indicator on the truck shows that he has traveled a total distance of 3.00 km during the ascent. Find the angle of incline of the hill.
Draw a picture To find θ, we use θ = sin-1(0.177) = 10.2o

Problem Solving Strategies Read the problem at least twice Draw diagram Identify data (knowns and unknowns) Choose equation(s) Solve equation(s) Evaluate and check answer

3. An airplane travels 450 km due east and then travels an unknown distance due north. Finally, it returns to its starting point by traveling a distance of 525 km. How far did the airplane travel in the northerly direction?
Draw a picture Use Pythagorean Theorem a2 + b2 = c2 = 270 km

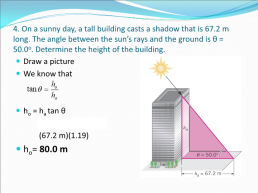
4. On a sunny day, a tall building casts a shadow that is 67.2 m long. The angle between the sun’s rays and the ground is θ = 50.0o. Determine the height of the building.
Draw a picture We know that ho = ha tan θ (67.2 m)(tan 50.0o) (67.2 m)(1.19) ho= 80.0 m

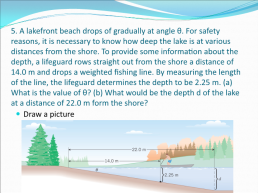
5. A lakefront beach drops of gradually at angle θ. For safety reasons, it is necessary to know how deep the lake is at various distances from the shore. To provide some information about the depth, a lifeguard rows straight out from the shore a distance of 14.0 m and drops a weighted fishing line. By measuring the length of the line, the lifeguard determines the depth to be 2.25 m. (a) What is the value of θ? (b) What would be the depth d of the lake at a distance of 22.0 m form the shore?
Draw a picture

A) We know So θ = tan-1 (0.161) θ = 9.15o B) For the bigger triangle, still but now we know θ = 9.15o and ha = 22.0 m So, ho = 3.54 m

Graphing Data
Graphs show information quickly and simply Independent Variable – the factor that is changed or manipulated during the experiment Plotted on the horizontal (x) axis Dependent Variable – the factor that depends on the independent variable Plotted on the vertical (y) axis Line of Best Fit – straight line drawn as close to all the data points as possible Linear Relationship Between 2 Variables y = mx + b m = slope b = y-intercept Slope =

Non-linear Relationships
Quadratic Relationship Between 2 Variables y = ax2 + bx + c A quadratic relationship exists when 1 variable depends on the square of another For ax2 + bx + c = 0 quadratic equation: Inverse Relationship Between 2 Variables A hyperbola results when one variable depends on the inverse of the other

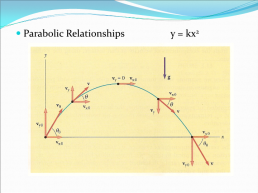
Parabolic Relationships y = kx2