Презентация - Теория вероятностей и статистика

Теория вероятностей и статистика

Цели:
Обучающая: повторить из курса 7 класса основные характеристики описательной статистики (среднее арифметическое, медиана, мода, размах числового ряда); показать прикладной характер математики к изучению окружающего мира. Развивающая: стимулировать познавательный интерес и развивать мыслительные способности, интерес к познанию. Воспитательная: воспитывать умение работать самостоятельно, коллективизм, трудолюбие и внимание к другим, умение воспринимать и анализировать информацию.

Результаты обучения:
- знать характеристики числового ряда; - вычислять моду, медиану, среднее арифметическое, размах числового ряда; - уметь использовать характеристики для описания числовых рядов.

«Статистика знает все… Известно, сколько какой пищи съедает в год средний гражданин республики... Известно, сколько в стране охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок... Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц!..» утверждали Ильф и Петров в своем знаменитом романе «Двенадцать стульев». Статистика (от лат. status — состояние) — наука, изучающая, обрабатывающая и анализирующая количественные данные о самых разнообразных массовых явлениях в жизни. Статистика позволяет описывать мир, окружающий нас, и явления повседневной жизни.

ЧТО ОЗНАЧАЮТ-все эти термины?
Статистические характеристики

Вспомним:
Что такое размах числового ряда ряда? Что такое среднее(среднее арифметическое) значение набора? Что такое медиана числового набора? Мода числового набора?
6, 17, 4, 5, 6, 1, 2, 8

Новые понятия:
6, 17, 4, 5, 6, 1, 2, 8
Как упорядочить ряд чисел? Записать числа так, чтобы каждое последующее число было не меньше (не больше) предыдущего Что такое размах числового ряда ? Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Что характеризует размах? Величину разброса наблюдаемых значений Может ли размах ряда равняться нулю?
1, 2, 4, 5, 6, 6, 8,17

Новые понятия:
Что такое среднее (среднее арифметическое) значение набора? Средним арифметическим называется частное от деления суммы этих чисел на число слагаемых.
Среднее арифметическое — это условная величина; она показывает центр рассеивания наблюдаемых величин (сумма отклонений от нее равна нулю), характеризует уровень наблюдаемых значений (это «среднее слагаемое») и общее количество всех наблюдаемых значений (температур, скоростей, высоты границы облаков).
1, 2, 4, 5, 6, 6, 8,17
Х = (1+2+4+5+6+6+8+17):8=49:8=6,125

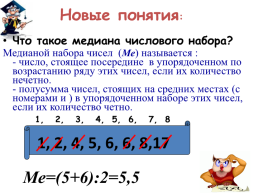
Новые понятия:
Что такое медиана числового набора? Медианой набора чисел (Ме) называется : - число, стоящее посередине в упорядоченном по возрастанию ряду этих чисел, если их количество нечетно. - полусумма чисел, стоящих на средних местах (с номерами и ) в упорядоченном наборе этих чисел, если их количество четно.
1, 2, 3, 4, 5, 6, 7, 8
1, 2, 4, 5, 6, 6, 8,17
Ме=(5+6):2=5,5

Новые понятия:
Мода числового набора? Модой числового ряда называется число, которое встречается в ряду чаще других. Мода характеризует чаще других встречающийся результат, это типичный результат для измерения. Сколько мод может иметь числовой ряд? Одну, несколько, ни одной Мо = 6
1, 2, 4, 5, 6, 6, 8,17

№17.1 (1) В городе пять школ. В таблице приведен средний балл, полученный выпускниками каждой из этих школ за экзамен по математике. Найдите средний балл выпускного экзамена по математике по всему городу?
Чтобы найти средний балл выпускного экзамена по математике по всему городу, нужно сложить баллы всех выпускников и поделить на общее количество выпускников. Общее количество выпускников равно 60+70+30+50+70=280 2. Если умножить количество учеников в школе на средний балл по школе , то получиться сумма баллов в этой школе, а если сложить все такие произведения , то сумма всех баллов по городу равна 60 60+70 54+30 68+50 72+70 54=3600+3780+2040+3600+3780= = 16800 3. Средний балл по городу равен 16800:280=60 Ответ: 60

№17.2 (2) В городе пять школ. В таблице приведен средний балл, полученный выпускниками каждой из этих школ за экзамен по математике. Найдите средний балл выпускного экзамена по математике по всему городу?
Чтобы найти средний балл выпускного экзамена по математике по всему городу, нужно сложить баллы всех выпускников и поделить на общее количество выпускников. 1. Общее количество выпускников равно 30+60+40+60+60=250 2. Если умножить количество учеников в школе на средний балл по школе , то получиться сумма баллов в этой школе, а если сложить все такие произведения , то сумма всех баллов по городу равна 30 66+60 55+40 60+60 64+60 58= 1980+3300 +2400+ +3840+3480= =15000 3. Средний балл по городу равен 15000:250=60 Ответ: 60

№18.1 (4) При каких значениях х медиана ряда чисел 1, 2, 3, 4, х будет равна 3.
Ранжируем данный ряд чисел в зависимости от значений х:
Если х <1, то х, 1, 2, 3, 4. Если 1 ≤ х < 2, то 1, х, 2, 3, 4. Если 2 ≤ х < 3, то 1, 2, х, 3, 4. Если 3 ≤х <4, то 1, 2, 3, х, 4. Если х >4, то 1, 2, 3, 4, х.
Ме = 2 Ме = 2 Ме = Х Ме = 3 Ме = 3
По определению медианой упорядоченного ряда из пяти элементов является третье по счету число. Найдем для каждого из этих пяти рядов медиану
Получили, что Ме = 3 при х ≥ 3

№18.2 (4) При каких значениях х медиана ряда чисел 11, 12, 13, 14, х будет равна 13.
Ранжируем данный ряд чисел в зависимости от значений х:
Если х <11, то х, 11, 12, 13, 14. Если 11 ≤ х < 12, то 11, х, 12, 13, 14. Если 12 ≤ х < 13, то 11, 12, х, 13, 14. Если 13 ≤х <14, то 11, 12, 13, х, 14. Если х >14, то 11, 12, 13, 14, х.
Ме = 12 Ме = 12 Ме = Х Ме = 13 Ме = 13
По определению медианой упорядоченного ряда из пяти элементов является третье по счету число. Найдем для каждого из этих пяти рядов медиану
Получили, что Ме = 13 при х ≥ 13

№19.1 (4) При каких значениях х среднее арифметическое ряда чисел 1,2,3,4,х будет равно 3.
Ряд чисел: 1, 2, 3, 4, х Среднее арифметическое: Х = 3 Запишем среднее арифметическое заданного ряда: Х =(1+2+3+4+х):5=(10+х):5=3. Решим уравнение: (10+х):5=3, х=5 Ответ: х=5

№19.2 (4) При каких значениях х среднее арифметическое ряда чисел 11, 12, 13, 14, х будет равно 1 3.
Ряд чисел: 11, 12, 13, 14, х Среднее арифметическое: Х = 13 Запишем среднее арифметическое заданного ряда: Х =(11+12+13+14+х):5=(50+х):5=13. Решим уравнение: (50+х):5=13, 50+х=65 х=15 Ответ: х=15