Презентация - Прямоугольный треугольник

ТРЕУГОЛЬНИК
П Р Я М О У Г О Л Ь Н Ы Й
учитель математики МБОУ СОШ № 4 г. Салехард
БУЛАННИКОВА НАДЕЖДА ВИТАЛЬЕВНА

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Содержание:
2. Свойства прямоугольного треугольника
1. Определение
3. Классический вид
4. Признаки равенства прямоугольных треугольников
5. Окружность, вписанная в треугольник
6. Окружность, описанная около треугольника
7. Подобие прямоугольных треугольников
8. Теорема Пифагора
9. Площадь прямоугольного треугольника
11. Пропорциональные отрезки в прямоугольном треугольнике
10. Формулы высоты прямого угла в прямоугольном треугольнике
12. Соотношения между сторонами и углами треугольника
13. Неравенство Коши
14. Решение прямоугольных треугольников
15. Задачи

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
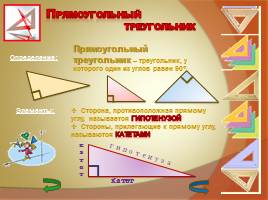
Определение:
Прямоугольный треугольник – треугольник, у которого один из углов равен 90°
Элементы:
Сторона, противоположная прямому углу, называется гипотенузой Стороны, прилегающие к прямому углу, называются катетами
гипотенуза
к а т е т
катет

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Свойства прямоугольного треугольника
В прямоугольном треугольнике любой из катетов меньше гипотенузы.
Сумма двух острых углов прямоугольного треугольника равна прямому углу.
По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
Две высоты прямоугольного треугольника совпадают с его катетами
Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Классический вид:
А
В
С
В
А
С
ɑ = ½ c
∠A=30° ∠B=60°
ɑ
c
∠C=90°
∠A=45° ∠B=45°
Равнобедренный треугольник
c
ɑ
ɑ
b

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
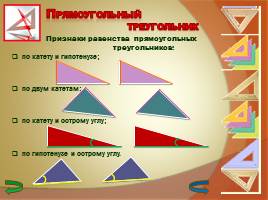
Признаки равенства прямоугольных треугольников: по катету и гипотенузе; по двум катетам; по катету и острому углу; по гипотенузе и острому углу.

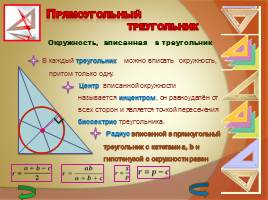
В каждый треугольник можно вписать окружность, притом только одну. Центр вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника. Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Окружность, вписанная в треугольник

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Окружность, описанная около треугольника
Около любого треугольника можно описать окружность.
Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.
У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
Радиус равен половине гипотенузы:
Радиус равен медиане, проведенной к гипотенузе:
a
b
c
mc
R

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
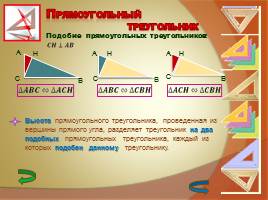
Подобие прямоугольных треугольников:
H
B
H
B
A
C
H
B
A
C
A
C
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Если дан нам треугольник, И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим И таким простым путем К результату мы придем.
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если длины всех трёх сторон прямоугольного треугольника являются целыми числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую
(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 1, 17),
(12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29)
(18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39),
(24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50), …
пифагорову тройку

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Площадь прямоугольного треугольника
B
C
A
A
B
C
Равнобедренный прямоугольный треугольник
ɑ
ɑ
ɑ
c
c
b
h

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Формулы высоты прямого угла в прямоугольном треугольнике
- высота из прямого угла a, b - катеты с - гипотенуза bc , ac - отрезки полученные от деления гипотенузы, высотой α, β - углы при гипотенузе
hc
Формула длины высоты через стороны
Формула длины высоты через гипотенузу и острые углы
Формула длины высоты через катет и угол
Формула длины высоты через составные отрезки гипотенузы

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Пропорциональные отрезки в прямоугольном треугольнике
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное (геометрическое) для отрезков, на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Соотношения между сторонами и углами треугольника
B
A
C
Противолежащий катет
гипотенуза
Прилежащий катет

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Неравенство Коши
Огюсте́н Луи́ Коши́ (барон Augustin-Louis Cauchy, 1789—1857) — знаменитый французский математик.
CD-высота, CO-радиус описанной окружности (медиана прямоугольного треугольника)
AD= a, BD= b, СD= h, CO= r .
r  h, притом данные отрезки совпадают, если треугольник ABC-равнобедренный.
Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
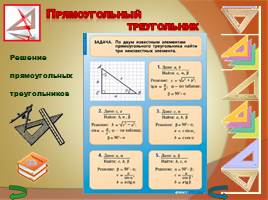
Решение прямоугольных треугольников

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
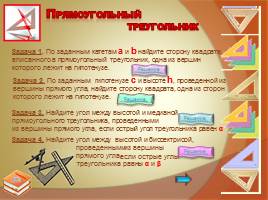
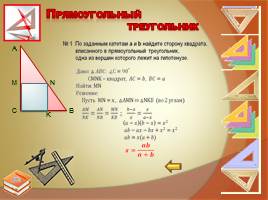
Задача 1. По заданным катетам a и b найдите сторону квадрата, вписанного в прямоугольный треугольник, одна из вершин которого лежит на гипотенузе.
Задача 2. По заданным гипотенузе с и высоте h, проведенной из вершины прямого угла, найдите сторону квадрата, одна из сторон которого лежит на гипотенузе.
Решение
Задача 3. Найдите угол между высотой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, если острый угол треугольника равен α
Задача 4. Найдите угол между высотой и биссектрисой,
Решение
Решение
Решение
проведенными
из вершины
если острые углы
прямого угла,
треугольника равны α и β

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
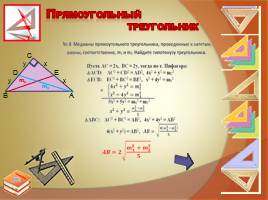
Задача 8. Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно,  m1 и m2 Найдите гипотенузу треугольника.
Задача 7. Найти площадь прямоугольного треугольника, если даны радиусы R и r описанного и вписанного в него кругов.
Решение
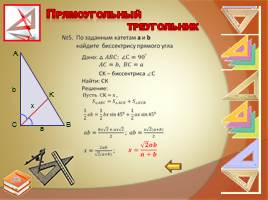
Задача 5. По заданным катетам a и b найдите биссектрису прямого угла.
Задача 6. Найдите угол между биссектрисами острых углов прямоугольного треугольника.
Решение
Решение
Решение

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
K
N
M
C
B
A

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
E
D
L
K
N
M
C
B
A
h

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
∠КСО = 900 - 2α

O
K
C
B
A

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
β
α
K
H
C
B
A

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
a
B
K
A
C
b
x

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
K
B
N
C
M
A
№ 6
135º, 45º

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
C
B
A
R
r
c
b
a

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
m1
m2
С
В
А
y
y
x
x
D
E

Интернет-ресурсы
http://www.azdekor.ru/Spektr/SREDN_SKOOL/MATEM/025/imagepage13.html
http://profmeter.com.ua/communication/learning/course/course7/contents/#LE364
http://www.hi-edu.ru/CentrDovusBooks/Geom/resheniya.pdf -
http://www.realschool.ru/news/188/
http://studentick.com/docs/index-10377.html
http://ru.wikipedia.org/wiki/%CF%F0%FF%EC%EE%F3%E3%EE%EB%FC%ED%FB%E9_%F2%F0%E5%F3%E3%EE%EB%FC%ED%E8%EA
http://uztest.ru/abstracts/?id=58&t=6
http://www.fmclass.ru/math.php?id=4850d63e8edde

Источник шаблона: Волкова Виолетта Евгеньевна, учитель начальных классов МАОУ лицей №21, г. Иваново Сайт: http://pedsovet.su/