Презентация - Урок-КВН «Цилиндр - Конус»

Воробьева Оксана Владимировна Преподаватель математики ГБОУ СПО «ЗАМТ» г. Заволжье

Тема: «Цилиндр. Конус».
Урок-КВН

1. Закрепить полученные знания по теме : «Цилиндр. Конус.» 2. Формировать положительное отношение к знаниям, прививать интерес учащихся к предмету. Показать связь между математикой и профессией. Воспитывать познавательную активность, культуру общения, культуру диалога. Развивать математическую грамотность речи, логического мышления.
Цели и задачи:

Домашнее задание Разминка Решение задач Конкурс капитанов
Конкурсы

Домашнее задание
Конкурс

Историческая справка : Конус в переводе с греческого "konos" означает "сосновая шишка".С конусом люди знакомы с глубокой древности.
Платон (428–348 гг. до н. э.) Много сделала для геометрии школа Платона, в частности, ей принадлежит: а) изучение конических сечений б) исследование свойств призмы, пирамиды, цилиндра и конуса

Демокрит (470 - 380 гг. до н. э.) - древнегреческий философ-материалист получил формулы для вычисления объема пирамиды и конуса.
Историческая справка

Аполлоний Пергский (260–170 гг. до н.э.) Большой трактат о конических сечениях был написан Аполлонием Пергским – учеником Евклида (III в. до н.э.), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Историческая справка

Детали машин , имеющие форму конуса:
Конические подшипники качения (коробка передач, оси колес) Камеры карбюратора Конические резьбы (система охлаждения)

Историческая справка : Слово цилиндр происходит от греческого слова , что означает “валик”, “каток”. С цилиндром люди знакомы с глубокой древности.
Архимед (287–212 гг. до н.э.) В 1906 году была обнаружена книга Архимеда “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа – Демокриту (470–380 гг. до н.э.) – древнегреческому философу-материалисту.

Платон (428–348 гг. до н.э.).
Много сделала для геометрии школа Платона. Платон был учеником Сократа (470–399 гг. до н.э.). В 387 г. до н.э. Платон основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона принадлежит исследование свойств цилиндра.
Историческая справка

Поршень Цилиндр Шейка коленчатого вала Шейка распредвала Амортизатор
Детали машин имеющие форму цилиндра

Разминка
Конкурс

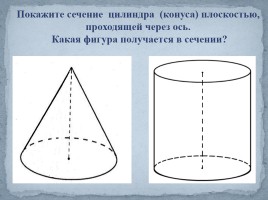
Покажите сечение цилиндра (конуса) плоскостью, проходящей через ось. Какая фигура получается в сечении?

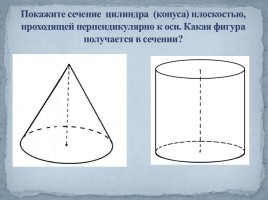
Покажите сечение цилиндра (конуса) плоскостью, проходящей перпендикулярно к оси. Какая фигура получается в сечении?

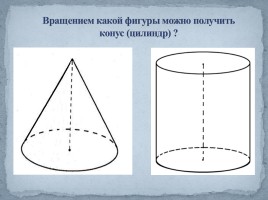
Вращением какой фигуры можно получить конус (цилиндр) ?

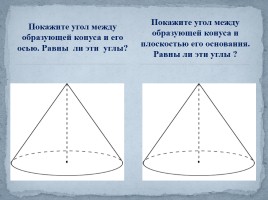
Покажите угол между образующей конуса и его осью. Равны ли эти углы?
Покажите угол между образующей конуса и плоскостью его основания. Равны ли эти углы ?

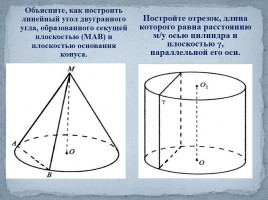
Объясните, как построить линейный угол двугранного угла, образованного секущей плоскостью (МАВ) и плоскостью основания конуса.
Постройте отрезок, длина которого равна расстоянию м/у осью цилиндра и плоскостью γ, параллельной его оси.

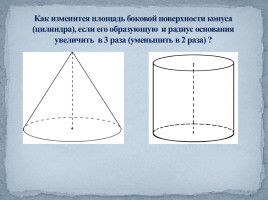
Как изменится площадь боковой поверхности конуса (цилиндра), если его образующую и радиус основания увеличить в 3 раза (уменьшить в 2 раза) ?

Конкурс
Решение задач

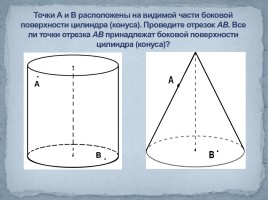
Точки А и В расположены на видимой части боковой поверхности цилиндра (конуса). Проведите отрезок АВ. Все ли точки отрезка АВ принадлежат боковой поверхности цилиндра (конуса)?

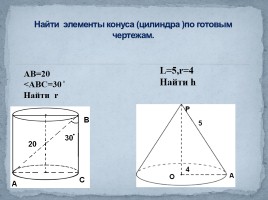
L=5,r=4 Найти h
Найти элементы конуса (цилиндра )по готовым чертежам.
АВ=20 <АВС=30 ̊ Найти r

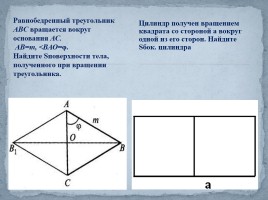
Равнобедренный треугольник ABC вращается вокруг основания АС. АВ=m, <ВАО=φ. Найдите Sповерхности тела, полученного при вращении треугольника.
Цилиндр получен вращением квадрата со стороной а вокруг одной из его сторон. Найдите Sбок. цилиндра

Капитанов
Конкурс

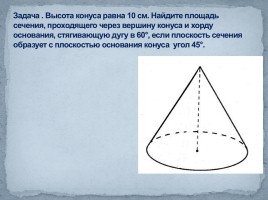
Задача . Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60°, если плоскость сечения образует с плоскостью основания конуса угол 45°.

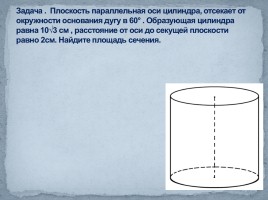
Задача . Плоскость параллельная оси цилиндра, отсекает от окружности основания дугу в 60° . Образующая цилиндра равна 10√3 см , расстояние от оси до секущей плоскости равно 2см. Найдите площадь сечения.

Подведение итогов
Название конкурса Количество баллов «Мерседес» Количество баллов «Каленвал»
Домашнее задание
Разминка
Решение задач
Конкурс капитанов
итого

Задача №555 (а) № 534 Вопрос 4 к главе 6. MATHEM_4_2_2_2_1_k_g_1.0.0.3.oms (сцены 1,2,3)
Домашнее задание:

http://krabov.net/11878-10-velikih-matematikov-10-foto.html https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcTspfNnc0ieOPzkSd26xf7vB3lJWaoyKVWDt4zX4_1iHoy9j7kLHA http://900igr.net/datai/algebra/Matematiki/0002-001-Arkhimed.jpg https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTqtFQFgJOTh5omDIP0GDUHTLQUUaWP-W7ZA_p0RZ_ueGbGSb5K http://img0.liveinternet.ru/images/foto/b/0/502/1415502/f_4819195.jpg
Интернет ресурсы