Презентация - Числовые последовательности - Прогрессии

Числовые последовательности
Прогрессии
Попкова Т.Г. МБОУ СОШ № 2 МО город Горячий Ключ

Определение:
Функцию y = f(x) , где x Є N, называют числовой последовательностью.
Способы задания:
1) Аналитически (формулой)
2) Словесно (описанием)
3) Рекурентно (по заданному первому члену последовательности, найти следующий)
4) Перечислением (указанием нескольких подрят идущих членов последовательности)
5) Графически.

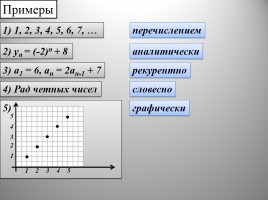
Примеры
1) 1, 2, 3, 4, 5, 6, 7, …
перечислением
2) yn = (-2)n + 8
аналитически
3) a1 = 6, an = 2an-1 + 7
рекурентно
4) Рад четных чисел
словесно
графически

Свойства последовательности
1) 1, 4, 9, 16, …
возрастающая
2) ½, 1/3, ¼, 1/5, …
убывающая
3) 6, 6, 6, 6, 6, …
стационарная
4) 1, - 1, 1, - 1, …
чередующаяся

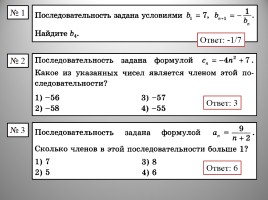
Ответ: -1/7
Ответ: 3
Ответ: 6

Арифметическая прогрессия
Числовая последовательность, в которой каждый её член, начиная со второго, получен из предыдущего прибавлением одного и того же числа, называется арифметической прогрессией
(an ) ÷
a2 = a1 + d , a3 = a2 + d, …, an = an-1 + d

d = a2 – a1 = … = an – an-1 - арифметическая разность
d > 0 возрастающая; d< 0 убывающая; d = 0 стационарная.
an = a1 + d( n – 1) – формула n –го члена
Имеет вид линейной функции y = kx + b an = d · n + m, nЄN.

Ответ: 2
Ответ: -29
Ответ: -28
Ответ: 5

Характеристическое свойство арифметической прогрессии
an = ( an-1 + an+1 ) : 2
Сумма n первых членов арифметической прогрессии

№ 1
Задайте формулой арифметическую прогрессию 3, 5, 7, 9, …
Ответ: xn = 2n + 1.
№ 2
Является ли число А = - 12 членом арифметической прогрессии an = - 3n + 2?
Решение:
- 3n + 2 = - 12, nЄN
- 3n = - 14
Ответ: не является.
Решение задач

№ 3
Найдите первые пять членов арифметической прогрессии заданной рекурентно b1 = 0,5 bn = bn-1 - 1.
Решение:
b2 = 0,5 - 1 = -0,5
b3 = -0,5 - 1 = -1,5
b4 = -1,5 - 1 = -2,5
b5 = -2,5 - 1 = -3,5
Ответ: 0,5; - 0,5; - 1,5; - 2,5; - 3,5.

№ 4
Найти d и a1 , если a3 = 9, a7 = 21.
Решение:
an = a1 + d( n – 1)
a3 = a1 + 2d = 9
a7 = a1 + 6d = 21
- 4d = - 12
d = 3
a1 + 2· 3 =9 a1 = 3
Ответ: d = 3, a1 = 3.

Ответ: 2.
Ответ: 1.
Ответ: 3.

Ответ: 4.
Ответ: 15.
Ответ: - 1.
Ответ: 1

Геометрическая прогрессия
Числовая последовательность, в которой каждый её член, начиная со второго, получается из предыдущего умножением на одно и то же bn ≠ 0
b2=b1·q; b3= b2·q = b1·q2; …; bn=b1·qn-1

q = b2 : b1 = b3 : b2 =…= bn+1 : bn -геометрический знаменатель
q ≠ 0
bn=b1·qn-1 – формула n – го члена
Имеет вид показательной функции y = m · qn , n Є N.
Если b1 > 0, q > 0, то при q > 1 (bn) – возрастающая; при 0< q <1 (bn) – убывающая.

Характеристическое свойство
bn2 = bn-1 · bn+1 среднее пропорциональное
Формула суммы n первых членов
1)Если прогрессия стационарная (q=1), то Sn = bn · n.
2)Если q≠1, то
3)Если |q |<1, то (bn)- бесконечная убывающая и

Ответ: 4.
Ответ: 48.
Ответ: -6.
Ответ: 0,5.

Ответ: 4.
Ответ: 364/9.