Презентация - Основы планиметрии - Отрезок и прямая

Основы планиметрии Отрезок и прямая

Возникновение и развитие геометрии.
Геометрия возникла в результате практической деятельности людей : нужно было сооружать жилища, храмы, прокладывать дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры.

Важную роль играли и эстетические потребности людей : желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.
В переводе с древнегреческого слово «геометрия» означает«земледелие» ( « гео» -земля , а «метро»- мерить).

За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.

Первым ,кто начал получать геометрические факты при помощи рас -суждений (доказательств), был древнегреческий ма -тематик Фалес (VI в.до н.э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном языке называется движением.

Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств. Попытки греческих ученых привести геометрические факты в систему начинаются уже в V веке до н.э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III веке до н.э.

Сочинение Евклида «Начала» почти 2000 лет служило основной книгой , по которой изучали геометрию . В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука. Эта книга была переведена на языки многих народов мира , а сама геометрия, изложенная в ней, стала называться евклидовой геометрией.

Что изучает геометрия?
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств : массы, цвета и т.д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.

Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать , ставить вопросы, анализировать , делать выводы , то есть логически мыслить.

Школьный курс геометрии делится на :
планиметрию
стереометрию
Планиметрия – это раздел геометрии, изучающий свойства фигур на плоскости ( от латинского слова «платинум» - плоскость и греческого «метрио» - измеряю). Примеры плоских фигур : отрезок , луч , прямая, угол, окружность, круг, треугольник, прямоугольник .
Стереометрия – это раздел геометрии, который изучает свойства фигур в пространстве. Примеры объёмных фигур : параллелепипед, шар, цилиндр, пирамида , конус…

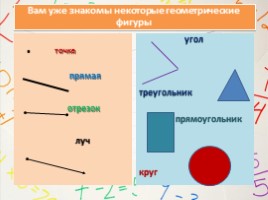
Вам уже знакомы некоторые геометрические фигуры
. точка прямая отрезок луч
угол треугольник прямоугольник круг

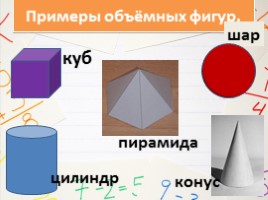
Примеры объёмных фигур.
куб
шар
конус
цилиндр
пирамида

Точки, прямые, отрезки
«Точка» в русском языке – конец заточенного гусиного пера.
A
C
B
D
«Точка есть то, что не имеет частей» Евклид
На рисунке изображены точки А , В , С и D.

Точки, прямые, отрезки

Прямая – множество точек, построенных с помощью линейки.

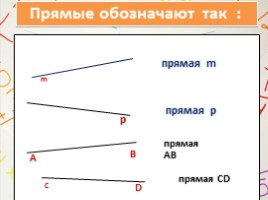
Прямые обозначают так :

m
прямая m
р
прямая р
А
В
прямая АВ
С
D
прямая CD

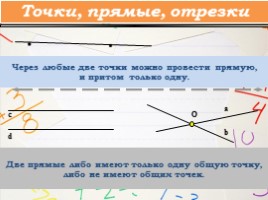
Через любые две точки можно провести прямую, и притом только одну.
c
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
.
.
d
Точки, прямые, отрезки

Отрезок – часть прямой, ограниченная двумя точками. Точки A и B – концы отрезка
A
B
Отрезок с концами А и В обозначают АВ или ВА. Он содержит точки А и В и все точки прямой, лежащие между точками А и В.
Точки, прямые, отрезки

Математический диктант.
1.Начертите прямую и обозначьте её буквой в. а) Отметьте точку М ,лежащую на прямой в. б) Отметьте точку Д , не лежащую на прямой в. в) Используя символы , запишите предложение : «Точка М лежит на прямой в , а точка Д не лежит на ней». 2. Начертите прямые а и в , пересекающиеся в точке К. На прямой а отметьте точку С , отличную от точки К. а) Являются ли прямые КС и а различными прямыми ? Ответ обоснуйте. б) Может ли прямая в проходить через точку С? Ответ обоснуйте.