Презентация - Уравнение касательной

10 КЛАСС
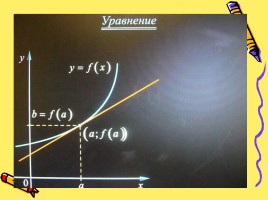
Уравнение касательной
ТЕМА УРОКА:

ЦЕЛИ УРОКА:
1. Уточнить понятие касательной к графику функции.
2. Вывести уравнение касательной.
3. Создать алгоритм составления уравнения касательной к графику функции y=f(x).
4. Начать отрабатывать умения и навыки в составлении уравнения касательной в различных математических ситуациях.

С f(x)=√(3-2x) f'(1)=?
Я f(x)=5/³√(3x+2) f' (-1/3)=?
Ю f(x)=12/√(3x²+1) f' (1)=?
Ф f(x)= 4√(3-2x²) f' (-1)=?
К f(x)=2ctg2x f' (-π/4)=?
И f(x)=4/(2-cos3x) f' (- π /6)=?
Л f(x)= tg x f' (π /6)=?
1 4/3 9 -4 -1 -3 5
РАСШИФРУЙТЕ, КАК ИСААК НЬЮТОН НАЗВАЛ ПРОИЗВОДНУЮ ФУНКЦИЮ

ОТВЕТ :
ФЛЮКСИЯ

Понятие "производная" возникло в связи с необходимостью решения ряда задач физики, механики и математики.
Честь открытия основных законов математического анализа принадлежит английскому ученому Ньютону и немецкому математику Лейбницу.
Лейбниц рассматривал задачу о проведении касательной к произвольной кривой.

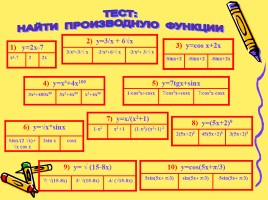
2) y=3/x + 6√x 2) y=3/x + 6√x 2) y=3/x + 6√x
3/x²+3/√ x -3/x²+6/√ x -3/x²+ 3/√ x
ТЕСТ: НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ
4) y=x³+4x100 4) y=x³+4x100 4) y=x³+4x100
3x²+400x99 3x3+4x99 x3+4x99
5) y=7tgx+sinx 5) y=7tgx+sinx 5) y=7tgx+sinx
1/cos2x+cosx 7/cos2x+cosx 7/cos2x-cosx
6) y=√x*sinx 6) y=√x*sinx 6) y=√x*sinx
Sinx/(2 √x)+ √x cos x 2sin x cosx
7) y=x/(x2+1) 7) y=x/(x2+1) 7) y=x/(x2+1)
1-x2 x2 +1 (1-x2)/(x2+1) 2
10) y=cos(5x+π/3) 10) y=cos(5x+π/3) 10) y=cos(5x+π/3)
5sin(5x+ π/3) sin(5x+ π/3) -5sin(5x+ π/3)
9) y= √ (15-8x) 9) y= √ (15-8x) 9) y= √ (15-8x)
7/ √(15-8x) 3/ √(15-8x) -4/ (√15-8x)
1) y=2x-7 1) y=2x-7 1) y=2x-7
x²-7 2 2x
8) y=(5x+2)9 8) y=(5x+2)9 8) y=(5x+2)9
2(5x+2)8 45(5x+2)8 3(5x+2)8
3) y=cos x+2x 3) y=cos x+2x 3) y=cos x+2x
Sinx+2 -Sinx+2 -Sinx+2x
3) y=cos x+2x 3) y=cos x+2x 3) y=cos x+2x
Sinx+2 -Sinx+2 -Sinx+2x

ОТВЕТЫ:
1) 2 2) 3 3) 2 4) 1 5) 2 6) 1 7) 3 8) 2 9) 3 10) 3

ДАВАЙТЕ ОБСУДИМ ПОНЯТИЕ КАСАТЕЛЬНОЙ. СОГЛАСНЫ ЛИ ВЫ С УТВЕРЖДЕНИЕМ: "КАСАТЕЛЬНАЯ - ЭТО ПРЯМАЯ, ИМЕЮЩАЯ С ДАННОЙ КРИВОЙ ЕДИНСТВЕННУЮ ОБЩУЮ ТОЧКУ"? 1) ДА 2) НЕТ

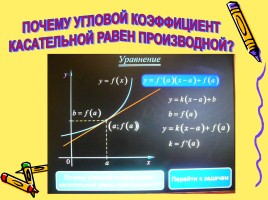
ПОЧЕМУ УГЛОВОЙ КОЭФФИЦИЕНТ КАСАТЕЛЬНОЙ РАВЕН ПРОИЗВОДНОЙ?

АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=f(x)
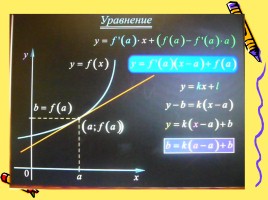
1. Обозначить абсциссу точки касания буквой а. 2. Вычислить f(a). 3. Найти f ' (x) и вычислить f '(a). 4. Подставить найденные числа а, f(a), f '(a) в формулу y = f(a) + f '(a) * (x-a)

ЗАКРЕПЛЕНИЕ
№ 828
Дополнительно:
2. Составить уравнение касательной к графику функции f(x)=х2-3х+5 в точке с абсциссой а=-1.
3. Составить уравнение касательной, проходящей через точку пересечения касательной графика функции f(x)=(3-x)/(x+1) с прямой у=1.
4. № 831 (а)
1. Устная работа : №809.

ЗАДАНИЯ С ЕГЭ: (НА ДОМ)
А. КАСАТЕЛЬНАЯ, ПРОВЕДЕННАЯ К ГРАФИКУ ФУНКЦИИ У=Х³-Х В ТОЧКЕ С АБСЦИССОЙ Х=0, ПАРАЛЛЕЛЬНА ПРЯМОЙ: 1) У=7-Х 2) У=Х-7 3) У=2Х-7 4) У=√3*Х+7 А. ДЛЯ ФУНКЦИИ У=4Х-Х² КАСАТЕЛЬНАЯ, ПАРАЛЛЕЛЬНАЯ ОСИ АБСЦИСС, ПРОВЕДЕНА ЧЕРЕЗ ТОЧКУ КАСАНИЯ: 1) (0;0) 2) (4;0) 3) (2;4) 4) (-1;-5) А. УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ f(x)= 2х²-3х-1, ПРОВЕДЕННОЙ В ТОЧКЕ С АБСЦИССОЙ Х0=1, ИМЕЕТ ВИД: 1)У=Х-3 2) У=Х-1 3) У=-2Х+3 4) 6У=-11Х-1 А. УРАВНЕНИЕ КАСАТЕЛЬНОЙ, ПРОВЕДЕННОЙ К ГРАФИКУ ФУНКЦИИ f (х)= 3х²-2х+5 В ТОЧКЕ А(2;13): 1) У=76Х-502 2) У=10Х-7 3) У=10Х+33 4) У=76Х-139 А. НАЙТИ ТАНГЕНС УГЛА НАКЛОНА КАСАТЕЛЬНОЙ, ПРОВЕДЕННОЙ К ГРАФИКУ ФУНКЦИИ У= 3Х²-5Х В ТОЧКЕ С АБСЦИССОЙ Х0=2. 1) 0,83 2) 2 3)3 4) 7