Презентация - Учебный проект по математике «Пропорция вокруг нас»

«Учебный проект по математике» «Пропорция вокруг нас»
Выполнила: Якутина Яна Ученица 6»А» класса Руководитель: Федотова А. В.

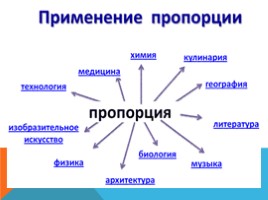
Цели работы:
1. Познакомиться с историей возникновения пропорции. 2. Рассмотреть применение пропорции в жизни. 3. Решить задачи на пропорцию.

Из истории
Понятие пропорции как равенства двух отношений чисел для целых чисел было дано в глубокой древности. Еще древние вавилоняне из рассмотрения подобных треугольников пришли к понятию пропорциональности сторон, выраженных в целых числах. Первыми арифметическую теорию пропорций разработали древнегреческий ученый пифагор (около 580-500 гг до н.Э.) И его ученики. Они рассматривали три вида пропорций: Арифметическую: а-в = с-d Геометрическую: a: b = c: d Гармоническую:   =   -

Им же принадлежит введение понятия непрерывной пропорции и среднего пропорционального из рассмотрения пропорции, у которой средние члены одинаковы. В 4 веке до н.э.  Древнегреческий ученый Евдокс (около 408 – 355 гг. до н.э.). Дал систематическое учение о пропорциях применительно не только к целым, но и к дробным числам. Интересно отметить, Евдокс был энциклопедистом своего времени. Он владел многими профессиями, был астрономом и механиком, математиком и авторитетным врачом. Строгая теория пропорций была построена в 3 веке до н.э. Древнегреческим геометром Евклидом в его знаменитых «началах», состоящих из 13 книг. Этой теории он посвящает 5 книгу. В основу своей теории Евклид положил учение евдокса. В настоящее время теория пропорций мало отличается от теории Евдокса – Евклида. Пропорцию Евклид формулирует так: четыре числа a, b, c и  d определяют пропорцию   = , если при любых целых числах m  и n при наличии ma ≤, ≥ nb имеем также mc ≥≤ nd.

Кулинария
Понятие пропорции используется в кулинарии. Когда мы готовим какое-либо блюдо, мы стараемся использовать то количество продуктов, которое указано в поварской книге. Это делается для того, чтобы не испортить блюдо. Если мы возьмём больше соли, то пересолим, а если меньше, то будет не вкусно. Ещё пропорция позволяет рассчитать количество продуктов для приготовления одного и того же блюда для разного числа гостей.

География
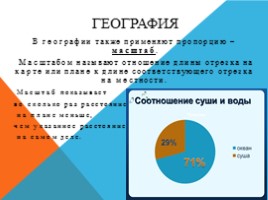
В географии также применяют пропорцию – масштаб. Масштабом называют отношение длины отрезка на карте или плане к длине соответствующего отрезка на местности. Масштаб показывает во сколько раз расстояние на плане меньше, чем указанное расстояние на самом деле.

Технология
На уроках технологии мы также используем пропорцию. Когда мы хотим сшить какую-либо вещь меньшего или большего размера, мы уменьшаем или увеличиваем выкройку до нужного нам размера. Например, выкройка фартука на себя и на куклу. Размеры элементов кукольного фартука отличаются от соответствующих размеров моего фартука в одно и тоже число раз.

Медицина
В медицинской практике врачи следят за тем, сколько и когда надо давать лекарства больному. В правильных дозах лекарство даёт лечебный эффект, в меньших – оно бесполезно, а в больших – приносит вред. При изготовлении лекарств тоже соблюдаются пропорции. Здесь необходима точность, так как при нарушении пропорций, составля- ющих лекарство ингредиентов, может получиться не лекарство, а яд. Отношения и пропорции используется также ваптеках при изготовлении лекарств и лечеб- ных напитков. Чтобы изготовить лекарственный препарат надо точно знать, сколько частей приходится на какую-либо часть.

Архитектура
При постройке храма в честь богини дианы римляне взяли пропорцию, которой отличаются стройные женщины: толщина колоны составила лишь 1/8 ее высоты. Благодаря этому колонны казалась выше, чем она была на самом деле,как раз за счет уменьшения толщины. В архитектуру вошли оба вида колонн, сохраняющие одна мужскую, другая женскую пропорции в отношениях между основанием и высотой. Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.3.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Химия
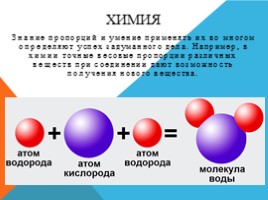
Знание пропорций и умение применять их во многом определяют успех задуманного дела. Например, в химии точные весовые пропорции различных веществ при соединении дают возможность получения нового вещества.

Физика
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – Примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.

«Золотая пропорция»
"Золотая пропорция" - это понятие математическое и ее изучение – это прежде всего задача науки. Но она же уже категория искусства и эстетики, которая изучает гармонию и красоту с математической точки зрения. Золотое число наблюдается в пропорциях гармонично развитого человека: длина головы делит в золотом сечении расстояние от талии до макушки. Кроме этого есть и еще несколько основных золотых пропорции нашего тела: расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1.618 расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618 расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618 расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618 расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618 расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618 расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618

Решите задачи
Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?

Решение
Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы. 5:100 или х:98. Получаем пропорцию: 5:100 = х:98. Х=(5·98):100; Х=4,9   Ответ: в 5кг арбуза содержится 4,9 кг воды.

Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?

Решение. Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти: 16,8:21 или х:35. Получаем пропорцию: 16,8:21=х:35. Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (21). Сократим дробь на 7. Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10)  и на 3 (168 и 3). Ответ: 35 литров нефти имеют массу 28 кг.

 После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение.  Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это: х:100 или 9:18. Составляем пропорцию: х:100 = 9:18. Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член (18). Сокращаем дробь. Ответ: площадь всего поля 50 га.  

Спасибо за внимание!
Спасибо за внимание!