Презентация - Леонардо Пизано Фибоначчи

Леонардо Пизано Фибоначчи 1170 г
материал подготовлен для сайта matematika.ucoz.com

Леонардо Пизано Фибоначчи
О жизни Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился предположительно в 1170 г. Его отец был купцом и государственным чиновником. Ему удалось
«устроить" своего сына, будущего математика Фибоначчи, в одно из арабских учебных заведений, где он и смог получить неплохое для того времени математическое образование.
материал подготовлен для сайта matematika.ucoz.com

До эпохи Возрождения было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих II, император Священной Римской империи. Фридрих II был внутренне глубоко далек от европейского христианского рыцарства. Рыцарские турниры Фридрих II совсем не признавал. Вместо этого он культивировал математические соревнования, на которых противники обменивались не ударами, а задачами.
На таких турнирах и заблистал талант Леонардо Фибоначчи
материал подготовлен для сайта matematika.ucoz.com

Некоторые проблемы, которые Император поставил перед знаменитым математиком, подробно изложены в Книге абака . Фибоначчи, очевидно, решил проблемы, поставленные Императором, и навсегда стал желанным гостем при Королевском дворе. Когда Фибоначчи перерабатывал Книгу абака в 1228 году, он посвятил исправленную редакцию Фредерику II. Всего он написал три значительных математических труда:
Леонардо Пизано Фибоначчи
Книга абака, опубликованная в 1202 году и переизданная в 1228 году, Практическая геометрия, опубликованная в 1220 году, и Книга квадратур. По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику чуть ли не до времен Декарта.
материал подготовлен для сайта matematika.ucoz.com

Книга об абаке
. Книга состоит из 15 разделов, которые последовательно трактуют: о новых знаках индусов и как с их помощью изображать числа; об умножении, сложении, вычитании и делении чисел; об умножении, сложении, вычитании и делении чисел с дробями; о нахождении цен товаров и об их обмене, правиле товарищества и о правиле "двойного ложного положения"; о нахождении квадратных и кубических корней; и, наконец, о правилах, относящихся к геометрии и о задачах алгебры .
Фибоначчи задумывал свое сочинение как пособие для купцов, однако по своему значению оно вышло далеко за пределы торговой практики, посуществу представляло своеобразную математическую энциклопедию эпохи средневековья.
материал подготовлен для сайта matematika.ucoz.com

Леонардо Фибоначчи любил гулять по лесу и размышлять. Например, о том, с какой геометрической прогрессией рождаются кролики. Неизвестно, долго ли он над этим думал, но именно размышляя о кроликах, придумал числовой, рад, каждое последующее число которого являлось суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 и так до бесконечности.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
Числа Фибоначчи
материал подготовлен для сайта matematika.ucoz.com

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
Числа Фибоначчи
Стоило Фибоначчи вывести эту закономерность, как ее проявления стали проявляться повсюду. Так как Фибоначчи любил гулять, первая закономерность бросилась ему в глаза на лесной поляне.
материал подготовлен для сайта matematika.ucoz.com

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
Числа Фибоначчи
на лесной поляне.
Понаблюдав, как прорастает из земли тысячелистник, ученый, к своему удивлению, обнаружил, что сначала появляется один листик, потом два, чуть позже – три, затем пять… восемь… тринадцать. И никогда по-другому!
Но тогда Фибоначчи даже не предполагал, насколько близко ему удалось приблизиться к разгадке одной из величайших тайн мироздания.
материал подготовлен для сайта matematika.ucoz.com

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
Числа Фибоначчи
Эта последовательность, получившая название ряда Фибоначчи, обладает удивительными свойствами. Отношение двух соседних чисел приближенно равно числу «фи», и чем дальше пара чисел находится от начала последовательности, тем точнее это приближение.
Ф=1.618
материал подготовлен для сайта matematika.ucoz.com

Божественная пpопоpция. Cpеди его совpеменных названий есть такие, как Золотое сечение. Kеплеp назвал это соотношение одним из "сокpовищ геометpии". Универсальный код Вселенной. Фибоначчи напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи. Самое важное математическое выражение природных явлений из всех когда-либо открытых.
Ф=1.618
материал подготовлен для сайта matematika.ucoz.com

Золотая пропорция — это такая пропорция, когда отрезок поделен на две части таким образом, что отношение большей части к меньшей равно отношению всего отрезка к большей части. Или наоборот.
Дроби можно переворачивать. В любом случае получится величина равная либо 1.61803399.., либо 0.61803399…
Золотая пропорция
материал подготовлен для сайта matematika.ucoz.com

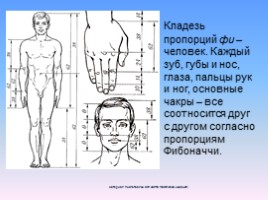
Кладезь пропорций фи – человек. Каждый зуб, губы и нос, глаза, пальцы рук и ног, основные чакры – все соотносится друг с другом согласно пропорциям Фибоначчи.
материал подготовлен для сайта matematika.ucoz.com

Наиболее интересно пропорция фи проявляется в спиральных структурах
материал подготовлен для сайта matematika.ucoz.com

Раковина улитки, цветок подсолнуха, рога животных, сосновые шишки и Галактика. Саморазвитие жизни происходит по спирали, которая стала символом эволюции.
спиральные структуры
Все природные спирали – это спирали Фибоначчи
материал подготовлен для сайта matematika.ucoz.com

«В геометрии существует два сокровища: первое – теорема Пифагора, второе – золотое сечение. Первое можно сравнить с мерой золота, второе – с драгоценным камнем». Кеплер
«Будущие ученые во все времена "будут отдавать свой долг Леонардо Пизанскому, как одному из величайших интеллектуальных первопроходцев мира".
Жозеф Гиз, главный редактор Британской Энциклопедии
материал подготовлен для сайта matematika.ucoz.com