Презентация - Мастер-класс «Решение задач по стереометрии»

Решение задач по стереометрии
Мастер- класс учителя математики МОУ «Аксеновская СОШ» Янгличевой А.Д.

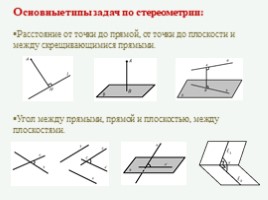
Основные типы задач по стереометрии: Расстояние от точки до прямой, от точки до плоскости и между скрещивающимися прямыми. Угол между прямыми, прямой и плоскостью, между плоскостями.

поэтапно-вычислительный(метод опорных задач ) (традиционный метод опирается на определения расстояния или угла, и требует от учащихся развитого пространственного воображения, применение данного метода состоит в применении известных опорных задач, которые в большинстве случаев формулируются как теоремы) метод координат (универсальный метод, может быть использован при решении задач любого вида) применение векторов (также может быть использован при решении задач любого вида) применение формул (площади ортогональной проекции многоугольника, объёма пирамиды, высоты треугольника, параллелограмма или трапеции).
Основные методы решения:

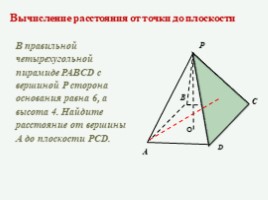
Вычисление расстояния от точки до плоскости
В правильной четырехугольной пирамиде PABCD с вершиной P сторона основания равна 6, а высота 4. Найдите расстояние от вершины А до плоскости PCD.
P
A
B
C
D
о

P
А
В
С
D
6
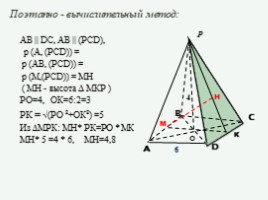
Поэтапно - вычислительный метод:
4
М
Н
к
AB || DC, AВ || (PCD), р (A, (PCD)) = р (АB, (PCD)) = р (М,(РСD)) = МН ( МН - высота Δ МКР ) РО=4, ОК=6:2=3 РК = √(РО ²+ОК²) =5 Из ∆МРК: МН* РК=РО * МК МН* 5 =4 * 6, МН=4,8
о

P
А
В
С
D
6
4
о
Метод объемов:
Пусть AН – искомое расстояние от A до(PCD). Рассмотрим пирамиду PАBCD, AН - ее высота V=1 ̸3S ADC *PO, V=1 ̸3S PDC * AН , S ADC *PO= S PDC * AН AН= S ADC *PO ̸ S PDC AН= (½*6 *6 *4) ̸ (½*6 *5) AН=4,8
Н

P
А
В
С
D
6
4
о
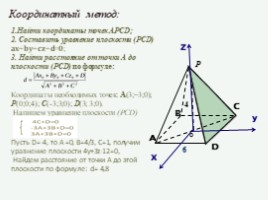
Координатный метод:
Z
У
Х
1.Найти координаты точек APCD; 2. Составить уравнение плоскости (PCD) ????????+????????+????????+????=????; 3. Найти расстояние от точки А до плоскости (PCD) по формуле: Координаты необходимых точек: А(3;−3;0); P(0;0;4); C(-3;3;0); D(3; 3;0). Напишем уравнение плоскости (PCD) Пусть D=-4, то A =0, B=4/3, C=1, получим уравнение плоскости 4у+3z-12=0, Найдем расстояние от точки А до этой плоскости по формуле: d= 4,8

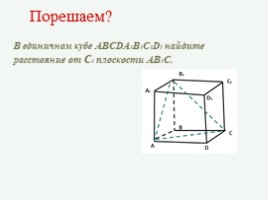
Порешаем?
В единичном кубе ABCDA1B1C1D1 найдите расстояние от C1 плоскости AB1C.

В
A
C
C1
B1
O1
A1
D
O
D1
Н
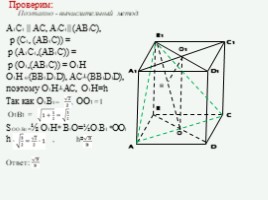
A1C1 || AC, A1C1|| (AB1C), р (C1, (AB1C)) = р (A1C1,(AB1C)) = р (O1,(AB1C)) = O1Н O1Н ℮(BB1D1D), AC┴(BB1D1D), поэтому O1Н┴AC, O1Н=h Так как O1B1= , OO1 =1 O1B1 = S OO1B1 =½ O1Н* B1O=½O1B1 *OO1 h , h= Ответ:
Проверим: Поэтапно - вычислительный метод:

В
A
C
C1
B1
O1
A1
D
O
D1
Н
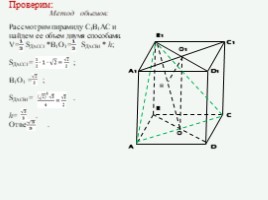
Рассмотрим пирамиду С1В1АС и найдем ее объем двумя способами. V=   SДACC1 *В1О1=  SДACB1 * h; SДACC1= ; В1О1 = ; SДACB1= . h= . Ответ:   .
Проверим: Метод объемов:

В
A
C
C1
B1
O1
A1
D
O
D1
Н
Рассмотрим прямоугольную систему координат с началом в точке С С(0;0;0), В1(1;0;1), А(1;1;0), С1(0;0;1). Составим уравнение плоскости. Проходящей через точки А, С и В1. Для этого подставим координаты этих точек в общее уравнение плоскости Ax + By +Cz + D = 0. Получим систему     или  Отсюда находим уравнение Ax –Ay – Az = 0; x – y – z = 0 По формуле находим расстояние от С1 до плоскости AB1C: d =  Ответ:   .
Проверим: Координатный метод:
Z
Х
У